Apollo16 登月区Hapke模型参数反演及模型敏感性分析

辛 欣，陈圣波，覃文汉，李东辉，陆天启，田粉粉

吉林大学地球探测科学与技术学院，长春 130026

0 引言

月表光度行为描述了月表物质反射的太阳光随入射、出射和太阳相角的变化[1]，其有差异表现为月表反射率高低不同，取决于月壤颗粒大小、粒子形状、透明度、孔隙度、表面粗糙度等因素[2]。月表光度行为研究是月球探测的重要目标之一，特别是对矿产资源勘探和着陆点选择具有重要的意义。随着人类探月技术的发展，越来越多的月球光谱数据被获取，为月表光度模型研究提供了数据基础，更加促进了月表光度特性研究。月表辐射传输模型的物理参数反演是用辐射传输模型进行光度校正的基础，对提高图像质量、月表矿物识别与反演以及分析着陆区光度异常现象原因有重要意义。由于月球登月点有限，采集的样品不能全面反映全月的月壤情况，因此通过反演光度模型参数分析月壤差异是一种了解月球的有效方法。

月表光度模型主要分为经验模型、几何光学模型和辐射传输模型。经验模型是通过观察实验而得出的定量模型，模型参数不具有明确的物理意义，如Minnaert 模型[3]。月表的几何光学模型为Shkuratov[4]于1998年提出，考虑到了土壤颗粒间的相互遮蔽情况，但较难考虑多次散射。辐射传输模型是基于辐射传输理论严格推导出的物理模型，模型参数具有明确的物理意义[5]。目前最常用的辐射传输模型为Hapke光度模型[6-7]。利用光谱数据反演月表Hapke模型参数分布，通过月表Hapke参数分布分析月表光度和物理特性，可以对月表地形有更深入的了解和认识[8]。Mcewen[9]于1996年利用Clementine数据通过拟合得到了部分月表Hapke模型参数，但由于参数太多可能会影响拟合效果，选择了固定模型中与热点有关的参数。Johnson等[10]于布卢姆斯堡大学测角仪实验室(Bloomsburg University Goniometer Laboratory)测量了Apollo 11、Apollo16土壤样品及模拟月壤的光度参数，验证了光度性质与反照率、颜色、粒度、表面纹理的相关性。随着越来越丰富的月球光谱数据的获得，Sato等[11]使用LROC(lunar reconnaissance orbiter camera) 宽角相机数据以1°×1°为一个像元单位，宏观上反演全月的Hapke模型参数并分析了月海月陆的光度差异，但每个像元对应约30 km×30 km的区域还是有很多差异未能体现。

在我们的工作中，考虑坡度、坡向，使用M3(moon mineralogy mapper)数据，利用Hapke光度模型反演Apollo16登月点附近区域1°×1°内的Hapke模型参数；与实验室测量的Apollo16 68810样品的Hapke模型光度参数进行比较，验证我们方法的有效性；通过研究区的模型参数差异和模型参数对反射率的影响程度，初步分析月壤物理性质差异及反射率差异原因。

1 反演方法

1.1 数据处理

M3是由美国国家航空航天局(NASA)制造的，搭载在印度探月卫星月船一号(Chandrayaan-1)上的高精度、高分辨率成像光谱仪[12]。卫星运行分为global模式和target模式。global模式尽量覆盖全月，空间分辨率为140 m，包括85个波段；target模式覆盖月球有限地区，空间分辨率为70 m，包括260个波段。本文使用global模式下的620 nm波段图像，选择Apollo16 登月点附近研究区域(14.089°E—15.066°E，8.016°S—9.160°S)的1B级M3数据。研究区高程如图1所示。

以LOLA(lunar orbiter laser altimeter) DEM(digital elevation model)为准，对M3G20090108T044645、M3G20090204T113444、M3G20090607T110414三幅M3数据进行配准，提取计算研究区域每个像素的坡度、坡向数据以及3个时相的入射角余弦、反射角余弦、相位角余弦和二分之一相位角正切值。并将1B级数据经辐射定标转换为辐射亮度因子(RADF)。

图1 研究区高程Fig.1 Elevation of the study area

1.2 模型构建

我们采用简化的Hapke光度模型[11]：

P(g)+H(cosis)H(cosiv)-1}。

(1)

式中：r(is,iv,g)为入射角为is、出射角为iv、相位角为g时的反射率；w为平均单散射反照率(the average single-scattering albedo，SSA)，w∈(0,1)；P(g)(phase function)表示颗粒的相函数，是介质中所有不同类型的颗粒，即不同大小、结构与组成的角散射函数的平均值[13]；BS(g)表示遮蔽相干效应(shadow hiding opposition effect, SHOE)；BS0表示SHOE的幅度；H(x)为表示多次散射的函数。

由于研究区域地形起伏较大，我们引入斜面入射角和出射角代替水平面的入射角和出射角[14]。对于水平面来说，平面法线垂直水平即为天顶方向，太阳照射平面到传感器接收辐射信息的过程中，太阳天顶角即为入射角；传感器天顶角为出射角。但是对于月球等行星表面凹凸不平、有坡度起伏的坡面来说，入射角为斜面上太阳入射方向与斜面法线的夹角，出射角为斜面上传感器接收方向与斜面法线的夹角。因此，式(1)中的入射角余弦cosis、出射角余弦cosiv为[15]：

cosis=cos[cosecosZ+sinesinZcos(φm-φs)]，

(2)

cosiv=cos[cosecosθv+sinesinθvcos(φm-φv)]。

(3)

式中：e为坡度；φm为坡向；Z为太阳天顶角；φs为太阳方位角；θv为仪器天顶角；φv为仪器方位角。

在最近的研究中，相函数P(g)一般采用双参数Henyey-Greens函数，表示为[16]

(4)

式中：形状参数b描述散射波瓣的形状，b∈(0,1)，b值较小时说明波瓣很低而宽，b值较大时说明波瓣高而窄；不对称参数c描述相函数前后散射的比例，c为负数时意味着粒子主要是向前散射，c为正数时说明粒子主要是后向散射。c与b的关系可用经验公式表示为[17]

c=3.29e-17.4b2-0.908。

(5)

BS(g)、BS0公式分别为[11, 18]：

(6)

(7)

式中：hS表示SHOE的角宽度，hS∈(0,0.18)；P(0)表示相位角为零时P(g)的值。H(x)公式为[18]

(8)

其中，

(9)

2 反演结果与分析

采用简化的Hapke模型式(1)，反演Apollo16 登月区附近Hapke模型参数w、b、hS，结果如图2所示。M3数据观测几何及反射率反演均方根误差如表1所示。w、b、hS反演结果显示，除个别像元外，该区域的b、hS变化很小，w有一定的变化。月壤颗粒大小、粒子形状、孔隙度、表面粗糙度、风化层填充物状态等因素的不同是造成研究区内参数差异的原因。参数w与月壤成分及粒径有关，与观测几何条件无关，是单位体积内各种不同尺寸粒子的综合贡献。参数b是相函数参数，与介质中所有不同类型颗粒的大小、结构与组成有关。由相函数参数b可经验得到相函数参数c。hS与月壤颗粒分布以及月壤孔隙度有关。

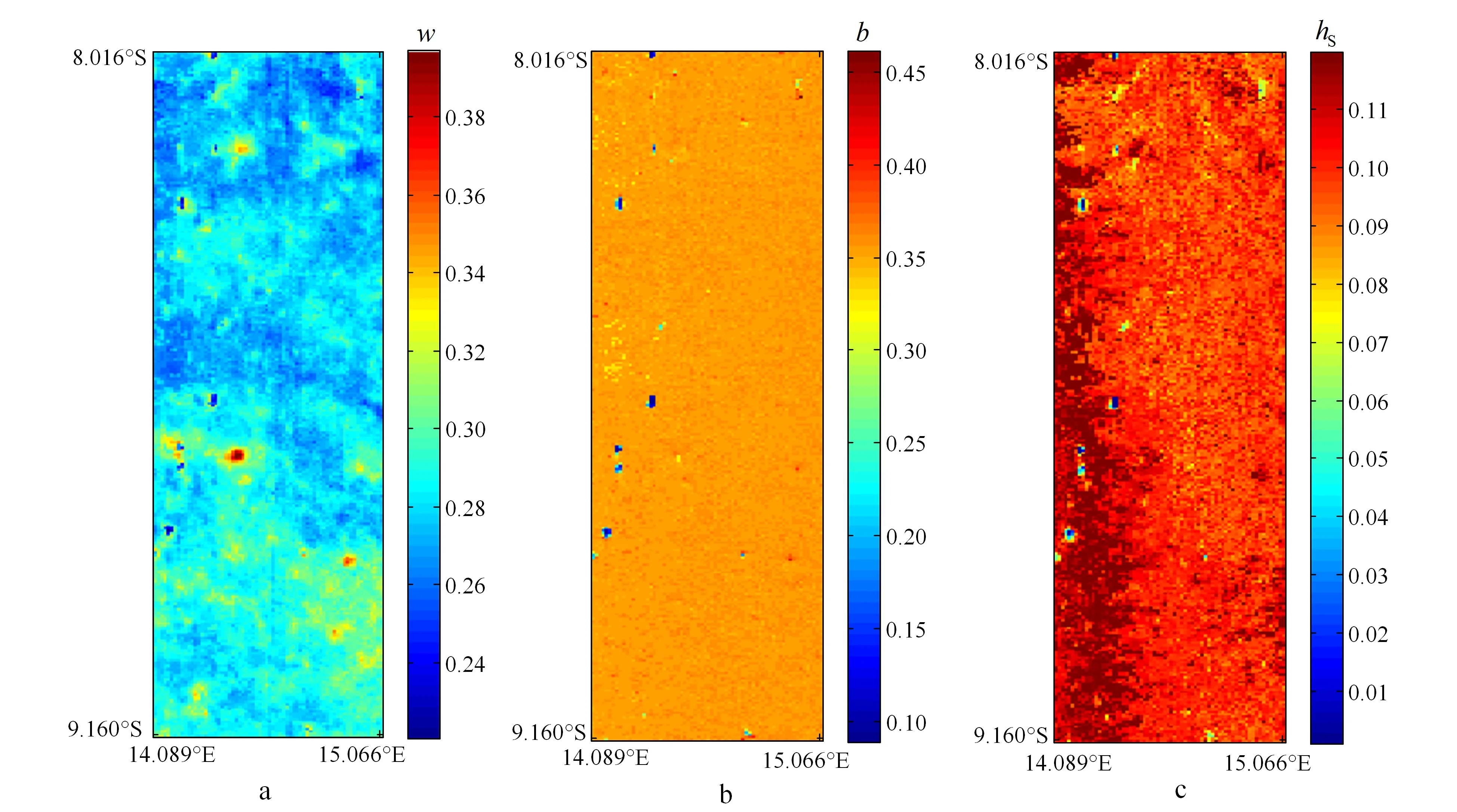
图2 光度参数反演结果Fig.2 Inversion results of photometric parameters

数据编号Z/(°)θv/(°)g/(°)辐射亮度反射率反演均方根误差M3G20090607T11041412.59～14.672.36～5.238.38～15.720.06～0.110.00M3G20090204T11344449.88～51.080.65～12.7938.08～53.950.05～0.150.01M3G20090108T04464522.57～24.080.38～11.7018.92～32.240.06～0.130.01

研究区内个别像元由于地形原因被阴影遮蔽，阴影遮蔽显现的低反射率造成参数反演存在奇异点。w、b、hS参数分布比例如图3所示。从图3可以看出：w为0.22～0.40，99%以上分布在0.25～0.35；b值99%以上分布在0.33～0.38；hS值99%以上分布在0.09～0.12。在本文研究区域，月壤中各矿物颗粒(包括不同大小、结构与组成等)散射函数的平均值变化不大，以及由反演b值计算得到的c值小于零，这表明在本文研究区域月壤中各类矿物颗粒的前向散射占主导地位。Johnson等[10]于布卢姆斯堡大学测角仪实验室测得550 nm 谱段Apollo16 68810土壤样品的w值为0.44、b值为0.334、h值(意义同hS)为0.062。可见，本文反演结果与Johnson等[10]实验室测量的Apollo16 68810土壤样品b值0.334及c值转化后小于零一致，hS反演结果略大于实验室测量模拟月壤与Apollo16样品h值，w反演值略小于Apollo16样品实验室测量w值。我们认为造成差异的原因可能是数据、模型版本和参数计算方法。此外,未扰动的风化层和搅拌样品表面的物理差异也有可能导致光度特性的改变[11]。

3 敏感性分析

反演Apollo 16登月区的光度参数后，我们需要知道不同光度参数对反射率的影响程度。简化后的模型式(1)包括w、b、hS3个光度参数。分析w对反射率的影响程度时，令b=0.35、hS=0.1、w的变化步长为0.05；分析b对反射率的影响程度时，令w=0.8、hS=0.1、b的变化步长为0.05；分析hS对反射率的影响程度时，令w=0.8、b=0.35、hS的变化步长为0.01。固定几何角度和地形(表2)，得到反射率随光度参数的变化曲线，结果如图4所示。

从图4可以看出：模型结果与模型参数w、hS正相关；3个参数中w对反射率的影响程度最大，hS对反射率的影响程度最小，反射率随hS的变化曲线相当平缓。

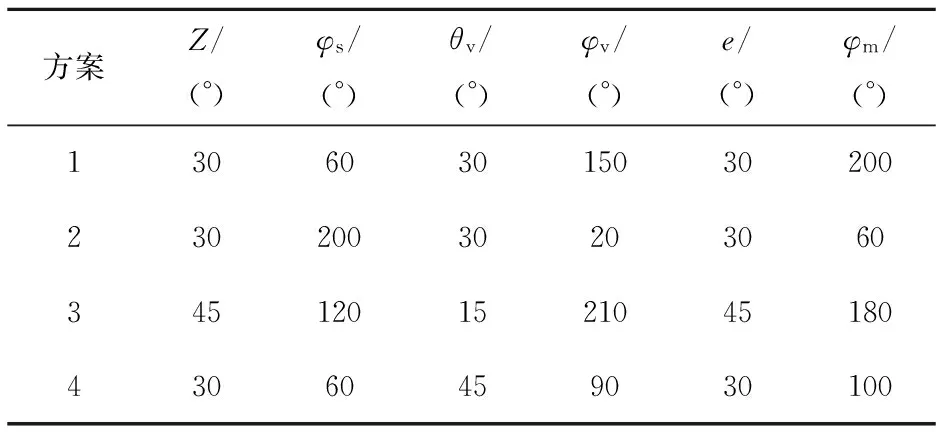
表2 参数组合计算方案

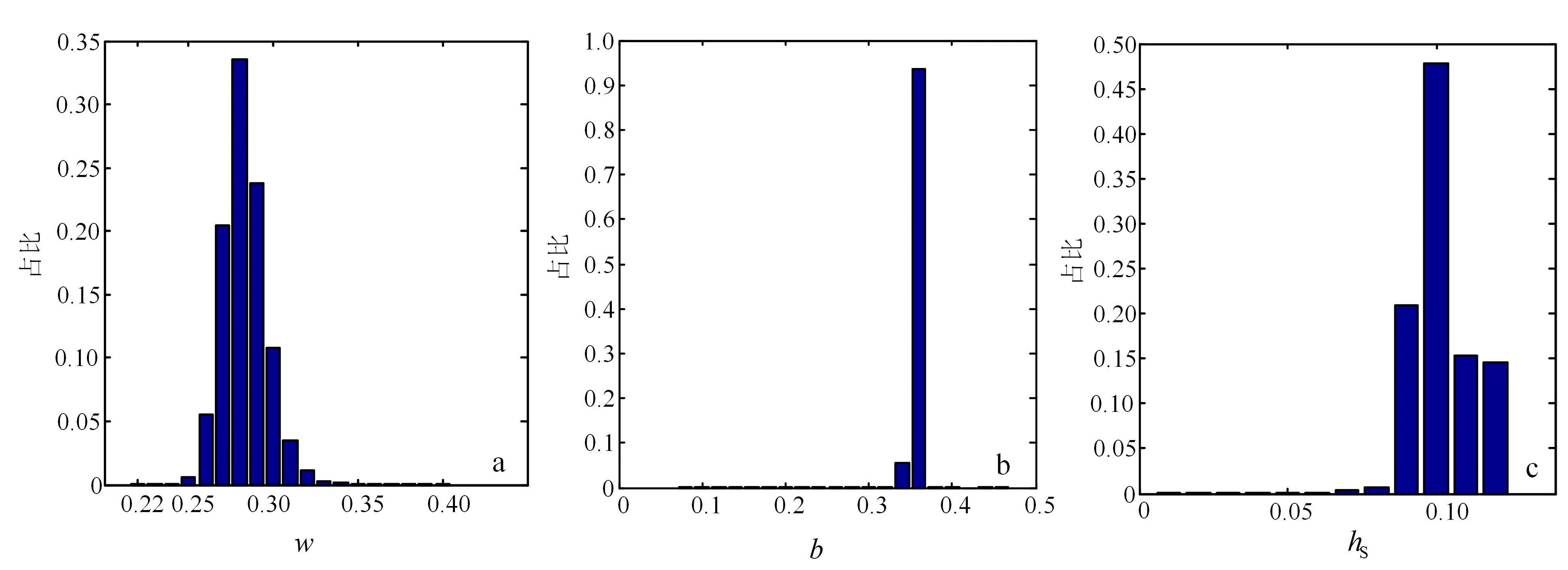
图3 参数分布比例Fig.3 Proportion of parameter distribution

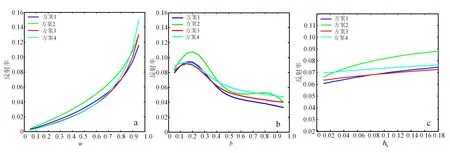
图4 反射率随不同光度参数的变化 Fig.4 Reflectance variation with different photometric parameter

4 结论

1)Apollo16 登月点附近研究区Hapke模型光度参数反演结果显示，除个别像元外，该区域的b、hS变化很小，w有一定的变化；表明该区域月壤中各类矿物颗粒的前向散射占主导地位，且月壤中各矿物颗粒(包括不同大小，结构与组成等)的散射函数的平均值与后向效应的宽度变化不大。

2)敏感分析表明光度参数w对月表反射率的影响最大，b次之，hS对反射率的影响程度最小，且反射率随着w值升高而增大。相同几何条件下本文研究区域反射率不同主要是由于w的影响。

3)由于w是月壤颗粒大小、风化层填充物状态、孔隙度及表面粗糙度等因素共同作用的结果，在研究区月壤颗粒大小相近的情况下，具体是风化层填充物状态、孔隙度及表面粗糙度中哪种因素造成本文研究区域内w值差异，有待进一步研究。

(

)：

[1] Hapke B.Theory of Reectance and Emittance Spec-troscopy[M]. 2nd ed. New York: Cambridge University Press, 2012.

[2] 张江, 凌宗成. 月球表面光度行为的地域依赖性分析[J]. 中国科学: 物理学 力学 天文学, 2013, 43(11): 1465-1469.

Zhang Jiang, Ling Zongcheng. Terrain Dependence of the Lunar Surface Photometric Behavior[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2013, 43(11): 1465-1469.

[3] Minnaert M. The Reciprocity Principle in Lunar Pho-tometry[J]. Astrophysical Journal, 1941, 93(3): 403-410.

[4] Shkuratov Y G, Kreslavsky M A.A Model of Lunar Photometric Function[C]// Lunar and Planetary Science Conference. Cambridge: NASA Astrophysics Data System, 1998.

[5] 李先, 陈圣波, 王旭辉,等. 基于辐射传输模型的水底反射率定量遥感反演研究[J]. 吉林大学学报(地球科学版), 2008,38(增刊1):235-237.

Li Xian, Chen Shengbo, Wang Xuhui, et al. Study Based in Radioactive Transfer Model of the Quantitative Remote Sensing of Water Bottom Reflectance[J]. Journal of Jilin University (Earth Science Edition), 2008，38(Sup. 1): 235-237.

[6] 崔腾飞. 月表矿物二向性反射模型研究[D]. 长春：吉林大学，2012.

Cui Tengfei. Study on Bidirectional Reflectance Model of Mineral on Lunar Surface[D]. Changchun: Jilin University, 2012.

[7] 张江, 凌宗成, 李勃,等.月球Reiner Gamma漩涡地区物质的光度行为及分类[J]. 岩石学报,2016, 32(1):113-118.

Zhang Jiang, Ling Zongcheng, Li Bo, et al. Photometric Behaviors and Classification of Reiner Gamma Swirl Materials[J]. Acta Petrologica Sinica, 2016, 32(1): 113-118.

[8] 许学森, 刘建军, 刘斌,等.月表光度模型研究进展[J]. 遥感技术与应用，2016 ,31(4):634-644.

Xu Xuesen, Liu Jianjun, Liu Bin, et al. Progress on Research of Lunar Photometric Model[J]. Remote Sensing Technology and Application, 2016, 31(4): 634-644.

[9] Mcewen A. A Precise Lunar Photometric Function[C]// Lunar and Planetary Science Conference. Cambridge: NASA Astrophysics Data System, 1996.

[10] Johnson J R, Shepard M K, Grundy W M, et al. Spectrogoniometry and Modeling of Martian and Lunar Analog Samples and Apollo Soils[J]. Icarus, 2013, 223(1): 383-406.

[11] Sato H, Robinson M S, Hapke B, et al. Resolved Hapke Parameter Maps of the Moon[J]. Journal of Geophysical Research: Planets, 2014, 119(8): 1775-1805.

[12] Boardman J W, Pieters C M, Green R O, et al. Measuring Moonlight: An Overview of the Spatial Properties, Lunar Coverage, Selenolocation, and Related Level 1B Products of the Moon Mineralogy Mapper[J]. Journal of Geophysical Research Atmospheres, 2011, 116(6): 100-114.

[13] Hapke B. Bidirectional Reflectance Spectroscopy: 1: Theory[J]. Journal of Geophysical Research, 1981, 86(B4): 3039-3054.

[14] 孟治国, 陈圣波, 崔腾飞,等. 基于嫦娥一号卫星激光高度计数据的月表有效反射率[J]. 吉林大学学报(地球科学版), 2010, 40(3):721-725.

Meng Zhiguo, Chen Shengbo, Cui Tengfei, et al. Effective Reflectivity of the Lunar Surface Based on the Laser Altimeter Data from the Chang’E-1 Orbiter[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(3): 721-725.

[15] Wang J, White K, Robinson G J. Estimating Surface Net Solar Radiation by Use of Landsat-5 TM and Digital Elevation Models[J]. International Journal of Remote Sensing, 2000, 21(1): 31- 43.

[16] 田丰. 全波段(0.35～25 μm)高光谱遥感矿物识别和定量化反演技术研究[D]. 北京：中国地质大学(北京), 2010.

Tian Feng. Identification and Quantitative Retrieval of Minerals Information Integrating VIS-NIR-MIR-TIR(0.35～25 μm) Hysoectral Data[D]. Beijing: China University of Geosciences (Beijing), 2010.

[17] Hapke B. Bidirectional Reflectance Spectroscopy: 7: The Single Particle Phase Function Hockey Stick Relation[J]. Icarus, 2012, 221(2): 1079-1083.

[18] Hapke B. Bidirectional Reflectance Spectroscopy: 5: The Coherent Backscatter Opposition Effect and Anisotropic Scattering[J]. Icarus, 2002, 157(2): 523-534.