基于环形扫面测量的三维直流电阻率法任意各向异性模型响应特征
殷长春,杨志龙,刘云鹤,张 博,齐彦福,曹晓月,邱长凯,蔡 晶
吉林大学地球探测科学与技术学院,长春 130026
0 引言
直流电阻率法已广泛应用于地球浅部矿产资源勘查、水文地质调查和环境工程领域[1]。它利用地表观测的电势分布,推测地下结构的电阻率分布[2]。随着野外采集仪器的快速发展以及数值算法和理论的不断完善,高精度和高效地求解复杂地电模型,尤其是任意各向异性地下模型的三维直流电阻率响应特征成为研究热点。目前正反演算法采用的电各项同性介质模型造成反演结果与地下实际地质情况存在很大差异[3],尤其是遇到具有层理面或裂缝的岩石等有方向依赖性的物质结构时,直流电阻率模型必须考虑地下电阻率各向异性[4-6]。
目前,人们已获得均匀半空间倾斜各向异性介质的电阻率响应解析解[7],而层状各向异性介质的电阻率响应已由Li等[8]和Yin等[4,9]给出。对于复杂的各向异性模型,目前的数值解法主要包括:积分方程法[10]、有限差分法[11]和有限元法[12]。其中:Li等[10]利用积分方程法计算了任意地下各向异性异常体的地面电势响应;王威等[12]利用有限元法在直流电阻率法正演模拟中计算各向同性介质中存在各向异性异常体时的电阻率响应。在有限元方法的应用中,非结构网格以其可以模拟任意形状异常体的突出优势备受重视,本文选择了基于非结构网格的自适应有限元算法来模拟地下任意各向异性异常体的电阻率分布特征。为保证源附近及电阻率差异较大区域的模拟精度,我们在非结构网格的基础上采用了基于梯度恢复的局部网格自适应加密技术,这不仅解决了全局网格自适应造成的内存较大、计算缓慢等问题,还可以根据经验对不同计算区域设定不同的单元误差阈值,提高了网格自适应加密的灵活性。
传统的电法勘探中采用的测量方式是只观测电场的一个同向分量,方位上的信息(垂直测线)往往被忽略。除此之外,视电阻率各向异性反常现象的存在使得单一测线所得到的视电阻率不能准确反映该方向的电阻率信息[4]。对于这种测量上的困扰,Yin等[13]在一维各向异性层状介质的视电阻率计算中采用了环形扫面测量方式,通过视电阻率极性曲线准确地反映了地下各向异性介质的方位信息。本文将该测量方法应用于三维各向异性地下介质的正演模拟中。利用二极装置,以点源为圆心,以收发距为半径,环形扫面测量多组共收发距各方位的电位信号,并且通过改变收发距以获得不同深度的地电信息,在实际应用中有很强的可操作性和灵活性。本文以浅部地表为研究目标,首先计算任意各向异性半空间模型电阻率响应,研究主轴电阻率旋转过程中视电阻率极性曲线随各向异性的分布特征;进而,我们在任意各向异性半空间中加入了任意各向异性异常体,通过对几种典型复杂各向异性模型的视电阻率分布特征进行分析,总结了识别围岩和异常体各向异性主轴电阻率和主轴方向的方法技术。
1 正演理论
1.1 电导率张量
对于任意各向异性地下介质,电导率σ(σ=ρ-1,ρ为电阻率张量)是一个含有6个独立分量的对称正定张量,即
(1)
式中:x、y、z分别代表直角坐标系的3个方向;σxy=σyx,σxz=σzx,σyz=σzy。根据Yin[6],该电导率张量可由主电导率张量经过3次欧拉旋转得到,即
σ=RTσcR。
(2)
式中:σc为主电导率张量,
(3)
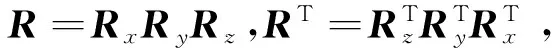
(4)
式中,α、β、γ分别是电导率主轴绕x、y、z轴的旋转角[6]。
1.2 基于二次场的边值问题
在三维半空间区域Ω中,地面Γ0上一点电源激发产生的电位u满足Poisson方程[1],地面边界处的电位满足Newman边界条件,区域其他边界Γ处的电位满足第三类边界条件,则二次场满足的边值条件表示如下:
·(σ·us)=-·((σ-σ0)·up),r∈Ω。
(5)
(6)
σ·up·n-
(7)
式中:up和us分别表示背景场电位和由异常体激发的二次场电位;r表示空间任意一点指向发射源的距离向量;σ0表示围岩电导率;n表示空间边界的法向分量;B和BP是中间量,B=rT·σ-1·r,BP=rT·σ0-1·r。一次场的解析解为[8]
(8)
在Hilbert函数空间H1(Ω)内取测试函数N,由Galerkin有限单元法可得
∭Ω(·(σ·us)+
(9)
我们使用开源代码TetGen[14]将区域剖分成Delaunay四面体网格,利用格林恒等式化简式(9)后代入边界条件,并对二次场在各单元中进行插值[15],得到线性方程组[16]
KUs=b。
(10)
式中:K是全局系数矩阵;b是右端源项;Us是待求的二次电位列向量。使用并行直接求解器MUMPS求解大型稀疏线性方程组可得到二次场电位,最后与背景场电位相加即可得到网格节点的总电位。在获得测点的总电位后,利用文献[17]给出的视电阻率定义即可计算相应的视电阻率。
1.3 基于梯度恢复的误差估计和局部网格自适应加密策略
Zienkiewicz等[18]于1987年提出了基于梯度恢复的后验误差估计算法(又称为Z-Z方法)。该方法实现起来简单、高效,不依赖于特定问题,故算法的可移植性较高,与非结构网格结合表现出很好的稳健性(robustness)[19]。
在L2范数下,三维恒定电流有限元计算中的单元误差可以表示为[17]
i=1, 2,,n。
(11)
式中:i表示单元编号;n表示目标区域剖分的单元总数;Ωi表示单元子区域;uF为有限元解插值得到的单元电位梯度;du是利用超收敛路径恢复技术[18]得到的与电位梯度精确值最为接近的单元梯度恢复值,即
du=Ga。
(12)
式中:
(13)
单元梯度恢复值在单元邻域(element patch)内求得,该邻域由与单元Ωi相邻的所有单元组成。通过求取式(13)中的a,可得到单元的恢复梯度值du,进而可求得区域内的单元误差‖e‖i。
在自适应网格加密策略中,我们首先设定每个目标区域的最大误差阈值:
‖e‖j;j=1,2,…,k。
(14)
式中,k表示目标区域数量。进而,可以求出每个单元一次迭代时的最大体积:
(15)
式中:Vi*表示单元原体积。式(15)表明自适应网格的体积可通过单元误差与最大误差比值进行调节。新的单元尺寸确定后,通过Delaunay网格剖分获得新的迭代网格,然后重复上述步骤直到单元误差小于对应区域的单元误差阈值为止。
由于全局自适应加密方法计算的是整个模型内的单元后验误差,在自适应过程中会对整个模型区域进行加密,而实际用到的数据只是整个区域中的部分区域,因此大量的网格数据不仅占用内存,而且会极大增加计算时间。本文在此基础上提出了局部自适应加密,将模型区域分为计算区域和扩边区域。扩边区域体积较大,单元剖分对计算结果影响较小,所以对扩边区域利用单元误差阈值直接代替单元误差,这样导致在网格的重新生成中该区域的单元基本保持原来的尺寸不变。对于计算区域,可以根据需要分为几个不同的区域,根据经验对不同区域设定不同的单元误差阈值,从而使得在网格重新生成的迭代过程中,不同区域的加密可不同,这样不仅可以减少不必要的内存浪费,还可有效地解决全局自适应加密的盲目性。
2 精度验证
本文算例运行平台为Intel(R) Xeon(R) CPU E5-2667 v3 @ 3.20GHz 3.20 GHz。我们首先采用如图1所示的任意各向异性的两层模型来验证本文算法的精度。为方便起见,采用电阻率进行讨论。第一层介质的主轴电阻率及欧拉角为ρx1=400m,ρy1=100m,ρz1=100m,α1=0°,β1=0°,γ1=0°;第二层介质的主轴电阻率及欧拉角为ρx2=40m,ρy2=10m,ρz2=10m,α2=0°,β2=0°,γ2=0°。假设点电源位于坐标原点,采用二极装置,通过与Wait[20]给出的半解析解对比,得到测量剖面的视电阻率和相对误差曲线(图2)。
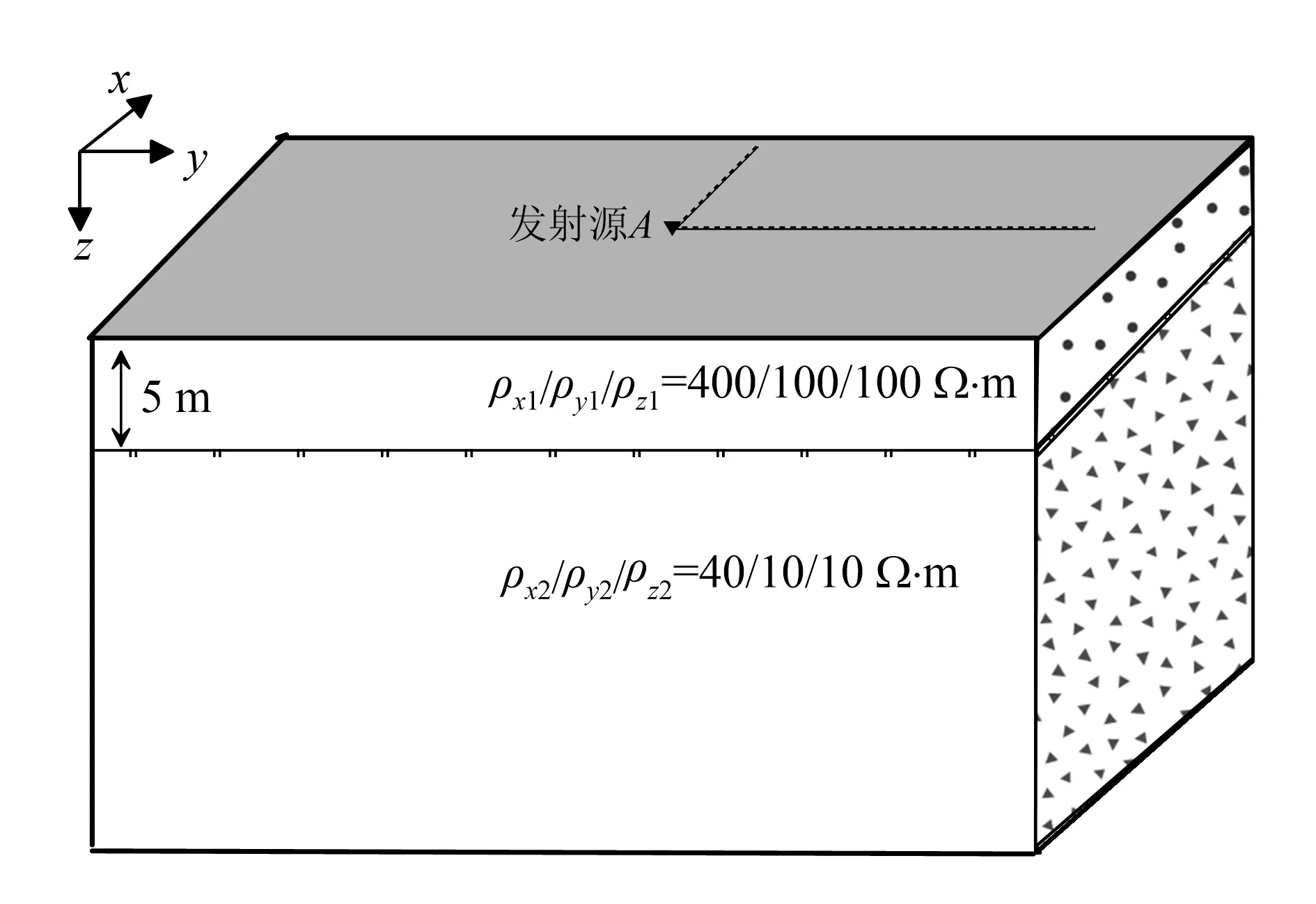
图1 两层各向异性地电模型Fig.1 Illustration of the two-layer model
通过分析图2可以得出如下结论:
1)有限元与半解析解的对比结果表明,本文算法具有较高的精度,能很好地满足正演模拟需求。
2)收发距较小时,浅部信息得到较好的反映;随着收发距增大,第二层电阻率得到越来越明显的反映。
3)在收发距较小时,x、y方向的观测结果发生分离,浅层的各向异性信息表现出来;而在收发距较大时,x、y方向的视电阻率也出现了分离,深部的各向异性信息表现出来。因此,通过改变收发距,层状大地各向异性特征可以求解。
4)在收发距小时,x测线方向视电阻率趋近于沿层理的电阻率ρL1=100m,y方向趋近于沿层理电阻率ρL1和垂直层理电阻率ρT1的几何平均值m;在收发距较大时,x测线方向视电阻率趋近于ρL2=10m,y方向视电阻率趋近于m。这实际上是典型的视电阻率各向异性反常现象[10](anisotropy paradox),即真实电阻率大的方向视电阻率小,而真实电阻率小的方向视电阻率大。
3 数值实验
3.1 模型建立
下面我们重点研究任意各向异性围岩和异常体视电阻率响应特征。为此,设定如图3所示的模型,建立z轴向下的直角坐标系,坐标原点位于地面中心,点电源位于坐标原点处;异常体的长宽高均为100 m,埋深5 m,主轴电阻率为ρx1=10m,ρy1=40m,ρz1=10m;围岩的主轴电阻率为ρx0=100m,ρy0=400m,ρz0=100m。在局部网格自适应加密过程中,我们选出600 m600 m600 m的计算区域,设定单元相对误差阈值为5%;

r. 收发距。a、b测线沿x轴;c、d测线沿y轴。图2 本文算法结果与半解析解对比及相对误差Fig.2 Comparisons of the result computed by this paper with semi-analytical solutions and the relative deviations
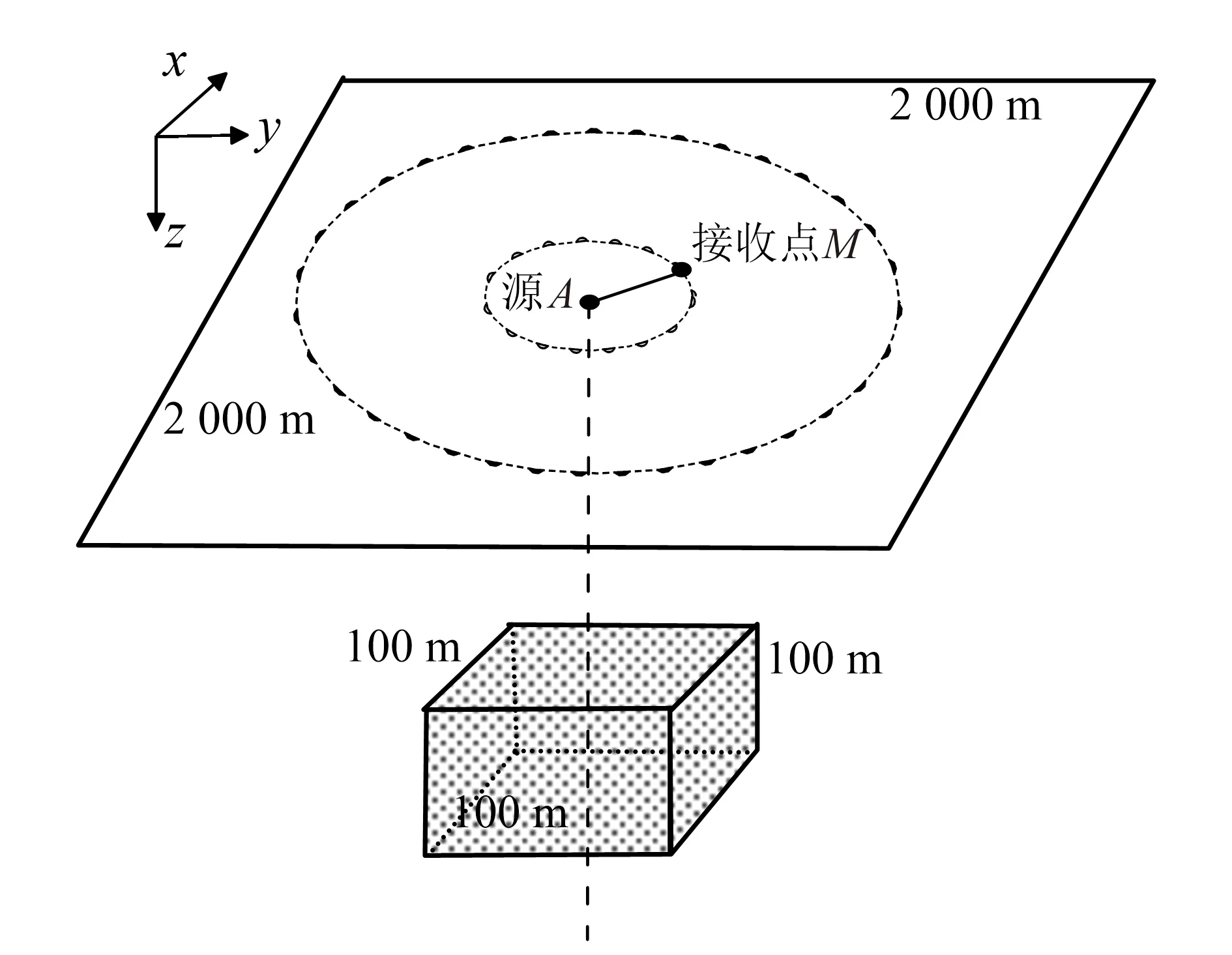
图3 基于二极装置的环形扫面测量与正演模型Fig.3 Concentric circular scanning measurement based on bipole configuration and 3D model
由于计算二次场,故对源的邻域和异常体所在区域设定单元误差为1%,计算区以外的扩边区域(范围为2 000 m2 000 m2 000 m)不加密。由于计算区域相对于整个模型区域很小,为了便于查看网格加密情况,本文仅展示600 m600 m300 m的区域内的y-z平面自适应加密网格(图4)。
对比图4中a、b、c可知,在局部自适应网格加密过程中,计算区域内部网格不断加密(而扩边区内部的网格基本不变),并且在第三次迭代后,计算区域的单元相对误差和异常体内部的单元相对误差已经达到要求。另外,观察图4c可以发现,由于设定的阈值各不相同,发射源附近区域和异常体内部加密程度要大于计算区内其他区域;异常体与围岩的交界处由于电阻率差异较大导致单元相对误差较大,网格加密程度较高。这是因为本文计算的是二次场,而二次场是由异常体与围岩交界处电阻率的突变所激发,因此异常体的表面相当于二次场的激发源,所以异常体表面单元相对误差比较大,对应的自适应网格加密比较明显。
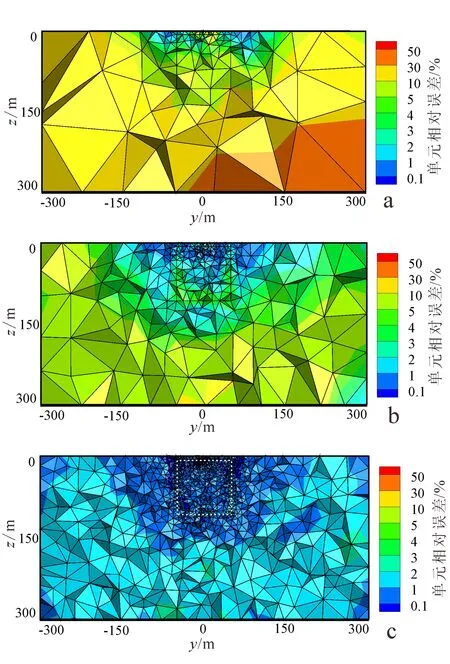
a.初始网格及单元相对误差;b.第一次自适应迭代加密后的网格剖分和单元相对误差;c.第三次自适应迭代加密后的网格剖分和单元相对误差,图中白色虚线方框内为异常体。图4 三维模型局部自适应加密网格Fig.4 Local adaptive mesh refinement for 3-D model
3.2 各向异性半空间模拟
我们首先研究各向异性半空间的视电阻率响应特征。为此,我们在正演模拟中假设异常体和围岩具有相同的各向异性,此时半空间的主轴电阻率为ρx/ρy/ρz=100/400/100m。图5为半空间主轴电导率绕z轴和x轴旋转时的视电阻率极性图。其中,由原点到各测点的距离表示视电阻率大小,而对应的方向表示实际测线方向。为简化起见,针对不同各向异性的网格图没有展示。
由图5a我们发现,视电阻率极性图呈现椭圆状,在主轴电阻率小的方向被拉伸(对应椭圆长轴),视电阻率大小为x与y方向的实际电阻率的几何平均值;在电阻率大的方向被压缩(对应椭圆短轴),视电阻率为x方向的实际电阻率。这正好与图2中的视电阻率各向异性反常现象相一致。利用这种视电阻率反常现象可以有效地识别目标体的各向异性特征。由图5b可以发现,当主轴电阻率绕x轴旋转时,视电阻率极性图也发生了改变:当旋转角度为0°时,地层层理直立,主轴电阻率为ρx/ρy/ρz=ρL/ρT/ρL=100/400/100m,x方向视电阻率等于m,y方向视电阻率等于ρx=100m;随着层理的倾斜,椭圆型曲线的短轴方向逐渐被拉伸,当旋转至90°时,主轴电阻率为ρx/ρy/ρz=ρL/ρL/ρT=100/100/400m,地层变成水平各向同性,视电阻率曲线呈现出圆形,半径为m。由于绕x轴旋转135°时,曲线与绕x旋转45°时的曲线相重合,故图中只展示绕x轴旋转45°时的曲线。从这些极性图可以明显看出,利用视电阻率长短轴的相对大小可以有效地判断各向异性特征和层理面的倾斜情况。
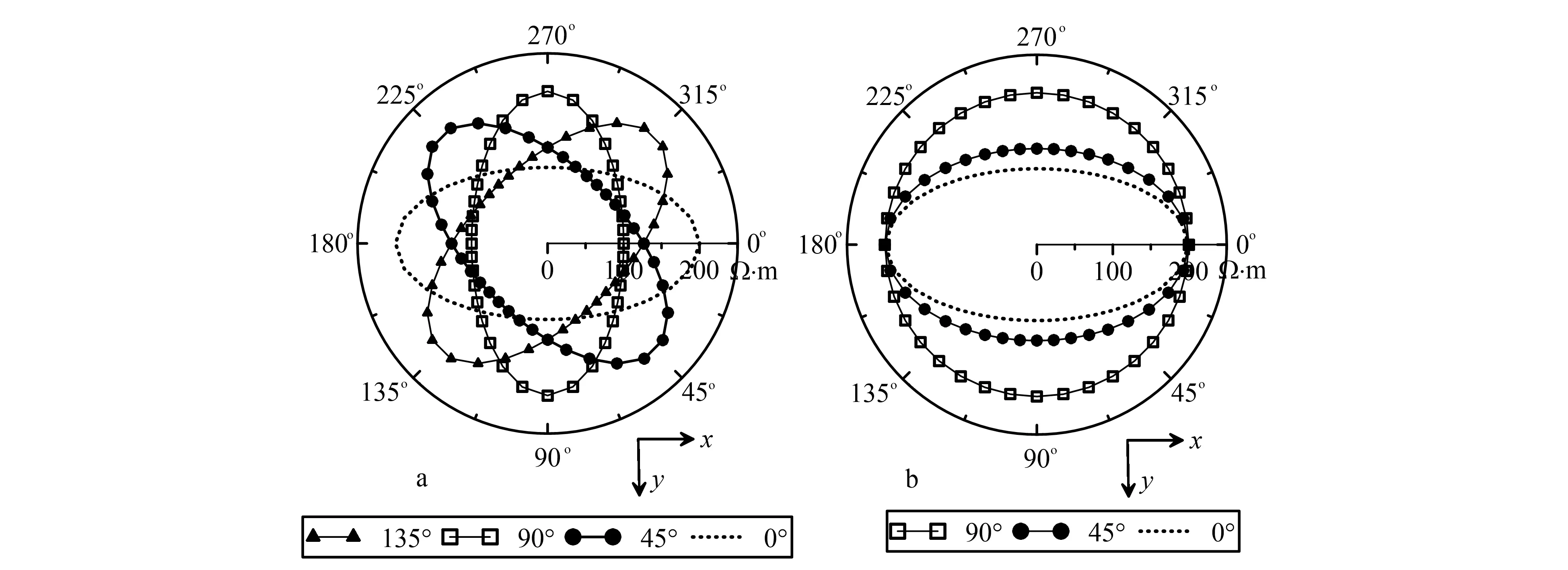
a.主轴电阻率绕z轴旋转0°、45°、90°、135°;b.主轴电阻率绕x轴旋转0°、45°、90°。图5 各向异性半空间视电阻率极性图Fig.5 Polarplots of apparent resistivity for an anisotropic half-space
3.3 含异常体的各向异性围岩模拟
图6展示了各向异性围岩和异常体主轴电阻率绕x和z轴旋转不同角度时的视电阻率极性图。这里围岩的主轴电阻率为ρx0=100m,ρy0=400m,ρz0=100m,而异常体的主轴电阻率为ρx1=10m,ρy1=40m,ρz1=10m。对于本文设计的模型(图3),当收发距较小(r=50 m)时,电阻率异常中心位置位于异常体内,主要反映异常体的电性特征;而当收发距较大时(r=140 m),电阻率异常不再关于异常体中心对称,主要反映围岩的电性特征。这为我们识别围岩和异常体各向异性提供了依据。
图6a描述的是异常体和围岩的主轴电阻率没有发生旋转时的视电阻率分布:小收发距对应的视电阻率在x方向被拉伸(长轴),在y方向被压缩(短轴),与图5中未旋转时的视电阻率分布特征一致;大收发距对应的视电阻率在x方向被拉伸(长轴),在y方向被压缩(短轴),与上述围岩半空间的视电阻率分布特征一致。图6b描述的是异常体主轴电阻率绕x轴旋转135°和围岩主轴电阻率绕z轴旋转45°时对应的视电阻率特征分布,与图6a相比:虚线表示的视电阻率短轴被明显拉伸,与图5中主轴电阻率绕x轴旋转135°时的分布特征一致;而实线相对于图6a沿顺时针方向旋转了45°,这与图5中主轴电阻率绕z轴旋转45°的事实一致。图6c描述的是异常体主轴电阻率绕x轴旋转90°和围岩主轴电阻率绕z轴旋转90°时的视电阻率分布,与图6a相比:由于此时异常体变成水平各向同性,所以虚线短轴被拉伸而成为圆形,与图5中主轴电阻率绕x轴旋转90°时的分布特征一致;实线电阻率分布相对于图6a沿顺时针方向旋转了90°,这与图5中主轴电阻率绕z轴旋转90°的情况一致。图6d描述的是异常体主轴电阻率绕z轴旋转90°和围岩主轴电阻率绕x轴旋转45°时的视电阻率分布,与图6a相比:虚线视电阻率沿顺时针方向旋转了90°,与图5中主轴电阻率绕z轴旋转90°的分布特征一致;相比之下,实线视电阻率相对于图6a短轴被拉伸,下方被拉伸程度大于上方,这是由于异常体存在造成的。图6e描述的是异常体主轴电阻率绕z轴旋转45°而围岩主轴电阻率绕x轴旋转90°时的视电阻率分布,与图6a相比:小收发距视电阻率绕顺时针旋转45°,与图5中主轴电阻率绕z轴旋转45°一致;而大收发距视电阻率的短轴被拉伸,呈现圆形分布,与水平各向同性围岩的视电阻率分布特征一致。图6f描述的是异常体主轴电阻率绕x轴旋转45°和围岩主轴电阻率绕x轴旋转135°时的视电阻率分布,与图6a相比:虚线短轴被拉伸,与图5中主轴电阻率绕x轴旋转45°时的分布特征一致;而实线短轴被拉伸,由于异常体的存在造成上方被拉伸程度大于下方,与围岩主轴电阻率绕x轴旋转135°的情况吻合。对比图6d和图6f还可以看出:围岩主轴电阻率绕x轴分别旋转45°和135°时,虽然视电阻率短轴均被拉伸,但由于旋转角度导致各向异性主轴方向不同,拉伸方向相反。这为有效地识别各向异性主轴电阻率旋转特征提供依据。
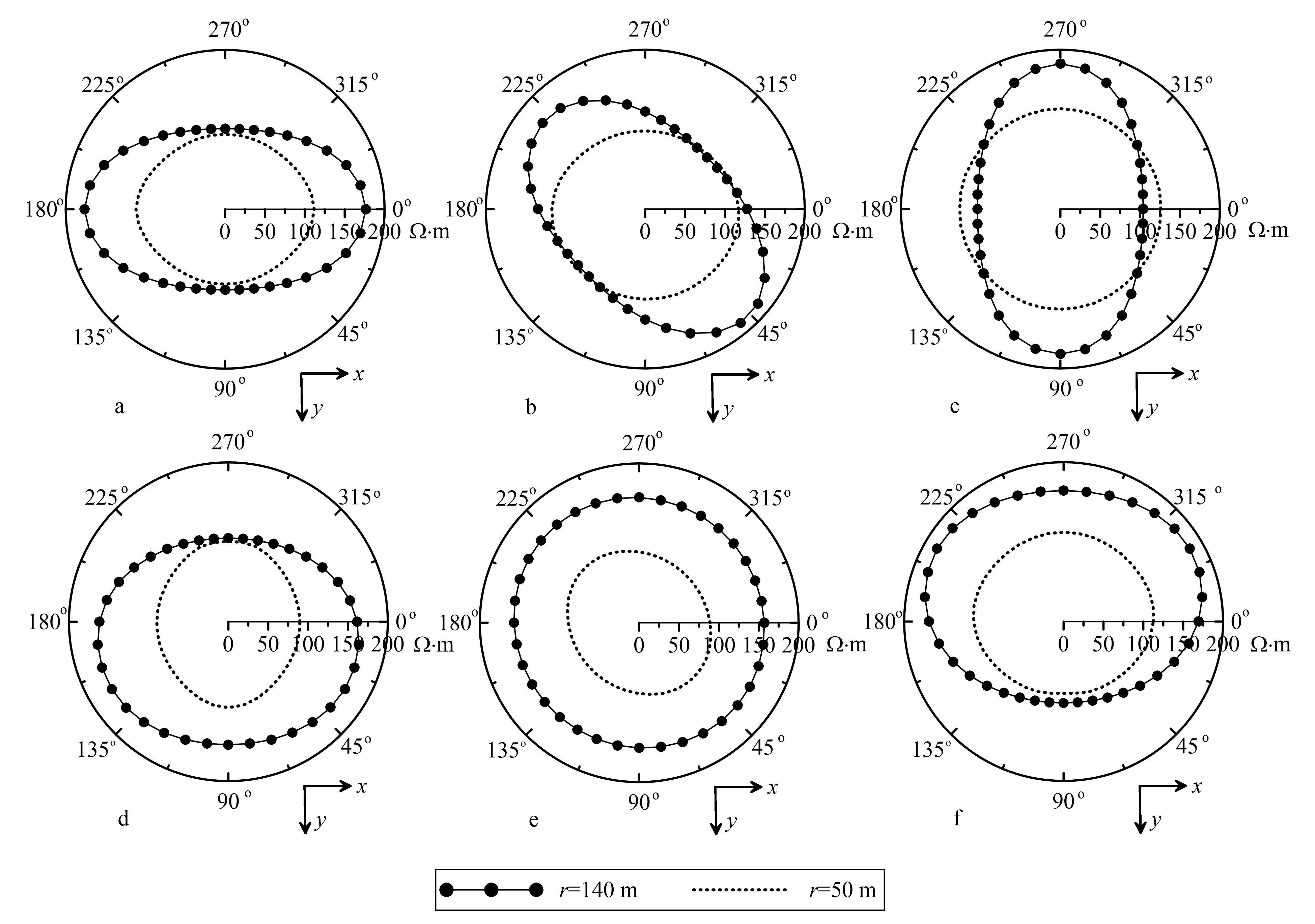
旋转角度:a. α0/β0/γ0=0°/0°/0°,α1/β1/γ1=0°/0°/0°;b. α0/β0/γ0=0°/0°/45°,α1/β1/γ1=135°/0°/0°;c. α0/β0/γ0=0°/0°/90°,α1/β1/γ1=90°/0°/0°;d. α0/β0/γ0=45°/0°/0°,α1/β1/γ1=0°/0°/90°;e. α0/β0/γ0=90°/0°/0°,α1/β1/γ1=0°/0°/45°;f. α0/β0/γ0=135°/0°/0°,α1/β1/γ1=45°/0°/0°。图6 各向异性半空间中存在各向异性异常体的视电阻率极性图Fig.6 Polarplots of the apparent resistivity for an anisotropic abnormal body embedded in an anisotropic half-space
4 结论
本文基于非结构网格自适应有限单元法,实现了各向异性情况下三维直流电阻率正演模拟,通过与一维层状介质各向异性响应对比验证了该算法的精度和有效性。通过采用环形扫描测量装置,对半空间任意各向异性介质视电阻率分布特征进行分析,并以此为参照对围岩和异常体各向异性的视电阻率响应特征进行分析,得出如下结论:
1)环形扫面测量方法可以有效识别大地各向异性电性分布特征。较之于传统的单测线测量的视电阻率,环形扫面测量结果可以更好地识别各向异性主轴方向和电阻率等参数。
2)环形扫面测量获得的视电阻率存在各向异性反常现象,在识别地下各向异性电性分布特征时需要引起注意。
3)利用本文提出的环形扫面技术,围岩和异常体的各向异性特征可以通过改变收发距分别进行识别。
本文对各向异性影响特征的研究和识别方法对于直流电阻率法在浅地表勘查领域的应用具有参考意义。
致谢:特别感谢对本文绘图和算法编写给予指导和帮助的博士研究生孙思源。
(
):
[1] 徐世浙,刘斌,阮百尧. 电阻率法中求解异常电位的有限单元法[J]. 地球物理学报, 1994, 37(2): 511-515.
Xu Shizhe, Liu Bin, Ruan Baiyao.The Finite Element Method for Solving Anomalous Potential for Resistivity Surveys[J]. Chinese Journal of Geophysics, 1994, 37(2): 511-515.
[2]Pain C C, Herwanger J V, Saunders J H, et al. Anisotropic Resistivity Inversion[J]. Inverse Problems, 2003, 19(5): 1081-1111.
[3] 刘斌,李术才,李树忱,等. 隧道含水构造电阻率法超前探测正演模拟与应用[J]. 吉林大学学报(地球科学版), 2012, 42(1):246-253.
Liu Bin, Li Shucai, Li Shuchen, et al. Forward Modeling and Application of Electrical Resistivity Method for Detecting Water-Bearing Structure in Tunnel[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(1): 246-253.
[4]Yin C, Weidelt P. Geoelectrical Fields in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 1999, 64(2): 426-434.
[5] 贲放,刘云鹤,黄威,等. 各向异性介质中的浅海海洋可控源电磁响应特征[J]. 吉林大学学报(地球科学版), 2016, 46(2):581-593.
Ben Fang, Liu Yunhe, Huang Wei, et al. MCSEM Response for Anisotropic Media in Shallow Water[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 581-593.
[6]Yin C. Geoelectrical Inversion for a One-Dimensional Anisotropic Model and Inherent Non-Uniqueness[J]. Geophysical Journal International, 2000, 140(1):11-23.
[7]Habberjam G. Apparent Resistivity, Anisotropy and Strike Measurements[J]. Geophysical Prospecting, 1975, 23(2):211-247.
[8] Li P, Uren N. Analytical Solution for the Point Source Potential in an Anisotropic 3-D Half-Space:Ι: Two- Horizontal-Layer Case[J]. Mathematical and Computer Modelling, 1997, 26(5):9-27.
[9] Yin C, Maurer H M. Electromagnetic Induction in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2001, 66(5): 1405-1416.
[10]Li P, Uren N. The Modelling of Direct Current Electric Potential in an Arbitrarily Anisotropic Half-Space Containing a Conductive 3-D Body[J]. Journal of Applied Geophysics, 1997, 38(1): 57-76.
[11] Wang T, Fang S. 3-D Electromagnetic Anisotropy Modelling Using Finite Difference[J]. Geophysics, 2001, 66(5): 1386-1398.
[12] Wang W, Wu X, Spitzer K. Three-Dimensional DC Anisotropic Resistivity Modelling Using Finite Elements on Unstructured Grids[J]. Geophysical Journal International, 2013, 193(2): 734-746.
[13] Yin C, Zhang P, Cai J. Forward Modelling of Marine DC Resistivity Method for a Layered Anisotropic Earth[J]. Applied Geophysics, 2016, 13(2):279-287.
[14]Si H. A Quality Tetrahedral Mesh Generator and Three-Dimensional Delaunay Triangulator[D]. Berlin: Weierstrass Institute for Applied Analysis and Stochastic, 2006.
[15] 金建铭, 电磁场有限元法[M]. 西安: 西安电子科技大学出版社, 2014.
Jin Jianming. The Finite Element Method in Electromagnetics[M]. Xi’an: Xi’an University Press, 2014.
[16]Ren Z, Tang J. A Goal-Oriented Adaptive Finite-Element Approach for Multi-Electrode Resistivity System[J]. Geophysical Journal International, 2014, 199(1): 136-145.
[17] 刘国兴. 电法勘探原理与方法[M]. 北京:地质出版社, 2005.
Liu Guoxing. Principals and Methods of Electrical Prospecting[M]. Beijing: Geological Press, 2005.
[18] Zienkiewicz O C, Zhu J Z. Super-Convergent Patch Recovery and a Posteriori Error Estimates: Part1: The Recovery Technique[J]. Internatioanl Journal for Numerical Methods in Engineering, 1992, 33(7): 1331-1364.
[19] 王飞燕. 基于非结构化网格的2.5-D直流电阻率法自适应有限元数值模拟[D]. 长沙:中南大学, 2009.
Wang Feiyan. 2.5-D DC Resistivity Modeling by the Adaptive Finite-Element Method with Unstructured Triangulation[D]. Changsha: Central South University, 2009.
[20]Wait J R. Current Flow into a Three-Dimensionally Anisotropic Conductor[J]. Radio Science, 1990, 25(5):689-694.

