分类讨论思想在含参函数中的应用

☉江苏省镇江中学 陈 蓬

分类讨论的思想是一种重要的数学思想方法，其基本思路是将一个较复杂的数学问题分解（或分割）成若干个基础性问题，通过对基础性问题的解答来实现解决原问题的思想策略.对问题实行分类与整合，分类标准等于增加一个已知条件，实现了有效增设，将大问题（或综合性问题）分解为小问题（或基础性问题），优化解题思路，降低问题难度.

分类讨论的常见类型主要有：（1）由数学概念引起的分类讨论：有的概念本身是分类的，如绝对值、直线斜率、指数函数、对数函数等；（2）由性质、定理、公式的限制引起的分类讨论；（3）由数学运算要求引起的分类讨论；（4）由图形的不确定性引起的分类讨论；（5）由参数的变化引起的分类讨论等.

常见分类讨论：指数函数y=ax底数，对数函数y=logax，直线中的斜率k，等比数列的公比q，分离系数，定义（等差数列、等比数列、奇偶性、圆锥曲线的定义等）引起的分类讨论，二次项系数，一元二次函数的判别式Δ，轴与区间的关系，零点大小，零点与区间的位置关系，端点函数值的大小，图像位置关系（上下方、交点），绝对值的分类谈论等.在分类讨论中我们要遵循不重不漏、层次分明、先易后难的原则，下面主要就分类讨论思想在含参型函数运用进行研究.

类型一、二次型分段函数中轴与区间位置关系、端点大小引起的分类讨论

例1设函数f（x）=|ax-x2|+2b（a，b∈R）.

（1）当b=0时，若不等式f（x）≤2x在x∈［0，2］上恒成立，求实数a的取值范围；

（2）若a为常数，且函数f（x）在区间［0，2］上存在零点，求实数b的取值范围.

分析：绝对值符号在函数问题中是常见的符号，可以通过正负分析法去绝对值符号，也可以通过绝对值不等式去绝对值，在二次含参型函数中，充分分析因参数引起的轴与区间的位置关系，在求最值时考虑端点取值的大小关系.

解：（1）当b=0时，若不等式x|a-x|≤2x在x∈［0，2］上恒成立.

当x=0时，不等式恒成立，则a∈R.

当0＜x≤2时，则|a-x|≤2在（0，2］上恒成立，即-2≤x-a≤2在（0，2］上恒成立.

因为y=x-a在（0，2］上单调递增，ymax=2-a，ymin＞-a，则

则实数a的取值范围为［0，2］.

（2）函数f（x）在［0，2］上存在零点，即方程x|a-x|=-2b在［0，2］上有解.

当a≤0时，则h（x）=x2-ax，x∈［0，2］，且h（x）在［0，2］上单调递增，所以h（x）min=h（0）=0，h（x）max=h（2）=4-2a，则当0≤-2b≤4-2a时，原方程有解，则a-2≤b≤0.

点评：在问题（1）中可以利用绝对值不等式去绝对值，从而进行分离变量，将不等式恒成立问题转化为最值问题，在问题（2）中首先根据a对二次函数图像的影响进行分类讨论，进而根据轴与区间的关系进行二次分类讨论，当0＜a＜2，根据单调性可以知道函数的最大值在区间端点，根据大小分析法解决函数的最大值，在解题过程在要遵循先易后难的原则.

类型二、多个函数因上下、左右位置关系引起的分类讨论

例2已知函数f1（x）=3|x-p1|，f2（x）=2·3|x-p2|（x∈R，p1，p2为常数）.函数f（x）定义为：对每个给定的实数x，f（x）=

（1）求（fx）=f（1x）对所有实数x成立的充分必要条件（用p1，p2表示）；

（2）设a，b是两个实数，满足a＜b，且p1，p2∈（a，b）.若（fa）=（fb），求证：函数（fx）在区间［a，b］上的单调递增区间的长度之和为（闭区间［m，n］的长度定义为n-m）.

分析：在读题的过程中，联想到函数f（1x）=3|x-p1|，f（2x）=2·3|x-p2|的图像，借助图像的位置关系是解决本题的关键.

解：（1）由（fx）的定义可知，（fx）=f（1x）（对所有实数x）等价于f（1x）≤f（2x）（对所有实数x），这又等价于3|x-p1|≤2·3|x-p2|，即3|x-p1|-|x-p2|≤3log32=2对所有实数x均成立（.*）

由于|x-p1|-|x-p2|≤（|x-p1）-（x-p2）|=|p1-p2（|x∈R）的最大值为|p1-p2|，故（*）等价于3|p1-p2|≤2，即|p1-p2|≤log32，这就是所求的充分必要条件.

（2）分两种情形讨论：

（i）当|p1-p2|≤log32时，由（1）知，（fx）=f（1x）（对所有实数x∈［a，b］），则由（fa）=（fb）及a＜p1＜b易知调性可知，函数（fx）在区间［a，b］上的单调增区间的长度为示意图如图1）.

图1

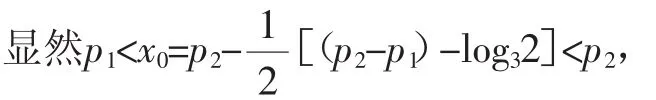
这表明x0在p1与p2之间.由⑴易知，

综上可知，在区间［a，b］上，

（示意图如图2）

图2

故由函数f（1x）及f（2x）的单调性可知，（fx）在区间［a，b］上的单调递增区间的长度之和为（x0-p1）+（b-p2）.

由于 （fa）=（fb），即3p1-a=2·3b-p2，得p1+p2=a+b+log32.②

故由①②得（x0-p1）+（b-p2）=b-

综合（i）（ii）可知，（fx）在区间［a，b］上的单调递增区间的长度和

分类讨论是数学解题的思想，通过层次分明、代数入微的书写，准确的表达才能增强解题过程的准确性，通过以上例题分析不难发现在解题过程中我们往往要借助数形结合思想才能使得分类讨论更加简洁和精准（含参型函数、数形结合分类讨论、代数书写），数形结合可以直观地揭示含参型函数问题本质，而数形结合又不能视为我们的解题过程，因此将数形结合能够通过分类讨论思想分析，进而进行代数化精准书写才是做此类问题的关键.H