陈题改编教学的实践性思考

☉安徽省太和县第一中学 吴 振

科学合理的教学策略才能促进学生在真正获得知识的同时发展智能、提高素质，学生充分发挥主体作用的情况下才能对数学学习展开理解性的学习，教师的知识与讲解是无法代替学生的理解与主动思考的.笔者结合“数列极限”复习课中的一道“陈题”对如何提高学生课堂参与度展开了实践性的思考与探索.

例题 已知一个等差数列和一个等比数列的首项都是1，等差数列的公差与前n项和分别是d和An；等比数列的公比与前n项和分别是r（|r|＜1）和Gn，记Sn=G1+G2+…

笔者让学生进行了尝试探究之后，结合自己的巡视组织了师生对此题的研讨与分析.

一、培养兴趣

师：字母众多往往会给学生造成繁难的感觉，数学问题的良好结构与完整叙述需要题设条件、解题依据、解题方法、题目结论这四个要素组成.同学们，为了解题顺利，请你们对这个例题改编一下试试看.

生1：已知一个等差数列的首项为1，公差为4，前n项和是An；一个等比数列的首项是1，公比是，前n项和是Gn，记Sn=G1+G2+…+Gn.

生2：把生1求极限的设计变成比较An和Sn的大小.师：生1的结论是显而易见的，生2所设计的大小的比较应注意0是否恒成立.（n≥2时，恒成立）

生3：已知一个等差数列的首项为1，公差为4，前n项和是An；一个等比数列的首项是1，公比是，前n项和是

生4：条件减弱为一样可以求出d.

师：生3和生4的结果相同，不过，生4将多余的条件删除掉了.相信大家一定能够运用类比的方法改编出有关求r的题目，这是给大家的课后作业.编题上大家可还有其他想法？

原命题中的条件与结论之间的逻辑关系在一定的改编之后能够得出新的命题.常用方式有：（1）增加条件；（2）去掉一些条件；（3）条件与结论互换；（4）更换角度思考与原命题等价的新命题等.学生在课堂中的尝试改编只是条件与结论的部分互换，引导学生进行命题的改编能为学生提出问题创造更多的机会.

二、纵深发展

生5：观察例题以及前面四位同学对例题的改编发现例题中的3个“1”之间的关系，如果1变成a，其他不变，求r，d.

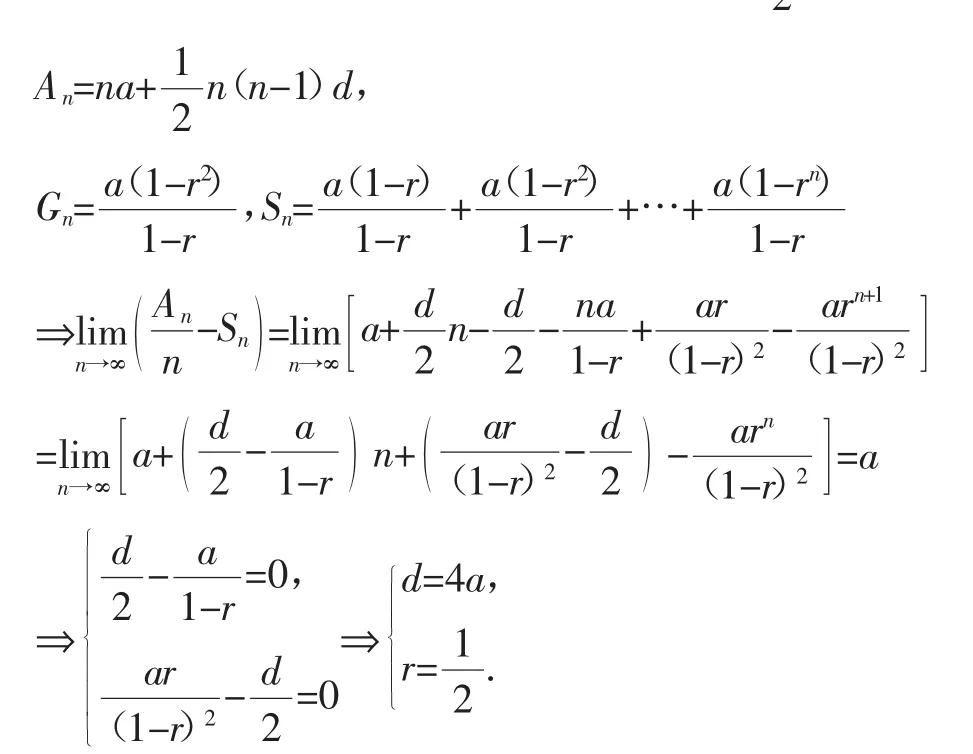
师：很好，生5发现了问题的本质使得本变式变得更有可操作性，生6的解题思路与结果也都是对的.还有其他的改编方法吗？

生7：我考虑将3个“1”中的2个“1”变成a，把存在，探求d与r的关系.

生8：将等差数列、等比数列的首项“1”分别改成a、b，极限值）=1中的“1”也改成a，其他条件不变，求d与r.

生9：我把极限存在，求d与r满足的关系式.

师：这三位同学在题目的改编上研究得更深，不过解题方法在实质上没有多大区别，其实“3个1”可以变化的方式很多，大家课后好好思考.高考试题其实大多都是根据一些例题或习题改编的，因此，同学们在平时的学习中应重视问题中的“并”和“串”，并使其中问题的来龙去脉清晰地呈现出来，大家在弄明白这些问题的本质与联系之后才能真正做到举一反三.

对原命题进行改编必须建立在吃透原命题的解题过程这一基础之上，在理顺解题思路的过程中从整体上概括出一般性才有可能在一定范围内达成知识的迁移与方法的运用，然后再根据一般性要素思考问题解决所需要的要素并设计出新的问题.

三、纵横联系

生10：记得之前我们做过这样的题目：首项是1的等差数列{an}的前n项和是Sn，等比数列{bn}的前n项和是Tn，且=9，求an与bn.我认为今天的例题是此题改编得到的.

师：很好.数学问题都具有很多前后左右的联系，我们在反思中要善于联想.生10在这一点上做得很好.

生11：我觉得大家改编时都没有涉及|r|＜1这一限制条件，如果去掉这一条件问题同样可求.

师：怎么求？

生11：分类讨论.

师：太棒了！我们应该从生11的思考中得到启示：题中每个词句及其含义都是审题中特别重要的，任何条件的存在自然都有一定的道理，下面请大家探究以下题为实数ai（i=1，2，…，n）与a的和方均值，对于集合A={-1，0，1}，若n=2013，ai∈A（i=1，2，…，2013），和方均值M=，a=1，且a+1a2+…+a2013=2，则a1，a2，…，a2013中零元素有______个.请大家看看此题可有矛盾？若有，在哪里？应该怎么纠正？

求证或求解的难度太大或过于抽象的原命题往往经过一定的特殊化处理更便于学生解决，有些原命题的解决并不是很难，但对其进行一定的改编能使学生对真命题的探索变得更有价值.

四、方法总结

数学教学离开例题教学是不完整的，教师应在传统的陈题中精心挑选出有价值的题目作为例题进行教学并帮助学生对基础知识、基本方法与技能的巩固与掌握，就题论题的教学一般会令学生陷入题海而倍感压抑，对原题进行深入的探究并进行题目价值与潜力的开发、挖掘与利用能使学生融会贯通地掌握知识，并在最短的时间内学会举一反三.

陈题改编应在反思解题过程、总结数学思想方法与思维策略的基础上进行适当的创新，这一教学行为能够很好地激发学生学习、研究、发明、创造的一系列潜在意识，对原题进行改编其实就是对原题的开发与挖掘，学生往往能在充分开发与利用原题潜在价值的过程中提升自己的理解能力、想象能力、逻辑思维能力及创造能力，因此原题的改编这一举措对于学生的发展是极有意义的.

陈题改编的过程对于学生来讲虽有一定的难度，但也是学生基本都能胜任的，不过学生自主改编出的新命题的真假也就不得而知了.因此，教师在陈题改编的教学过程中应促进学生之间的交流讨论与思想碰撞，不断启发学生的思想火花并体验学习的信心、兴趣与乐趣，这是改编陈题教学过程中最为重要的.

教学分层与教学个性化常常会在陈题改编的交流与讨论中得以实现，层次性与递进性是陈题改编教学过程中尤其应该体现的，那些能够让学生“跳一跳”都能够得上的高度能够促进全体学生的发展，同时，学生在改编陈题的过程中也能感悟数学问题的由来以及数学问题的解决方法，学生在数学知识间的联想能力也能得到很好的培养，在陈题改编的过程中逐步树立起自觉研究数学问题的意识.

教师在陈题改编之后还应该引导学生进行交流，这一过程可以简单概括为“说数学”，说什么、怎么说以及为什么这么说都是这一过程中需要搞清楚的重要内容.教师在面对面的交流中能够更好地了解学生对知识理解的差异、思维上的优势以及认知方面的特点与不足，根据学生的表述作出及时的评价并对自己的教学实践作出诊断与反思，从而形成一套更加符合学生个性发展与思维特点的教学方法.

陈题改编的成果也是需要教师与学生再次审视与思考的，学生在重新审视的过程中能够更加深刻而清晰地理解原题中的条件和结论，从而修正他们“数学学习只是做数学”的错误认知.F