基于动态传动误差的齿廓修形直齿轮动态特性分析

柯恒一,刘翰林

(武汉理工大学 能源与动力工程学院，湖北 武汉 430070)

0 引言

直齿轮是最为常见的一种齿轮传动形式，在实际工作中，直齿轮的轮齿受到啮合力作用产生弹性变形，导致在轮齿啮入啮出的临界位置产生干涉现象。齿轮副的啮合干涉是齿轮传动系统产生振动和尖峰动载荷的主要原因之一，且在高速重载下，齿面瞬时接触温度很高，啮入啮出产生的齿面刮痕切屑会堆积至节圆附近，加速齿面的磨损和胶合失效。因此需要对直齿轮进行齿廓修形，即根据直齿轮副啮入啮出干涉情况、边缘接触情况，在主动轮或从动轮工作齿面上去除一小部分，使得直齿轮副啮入啮出临界点避开齿顶棱边，尽可能地保证直齿轮副始终处于完整的共轭啮合状态。直齿轮修形的概念首先由Walker[1]于1938年提出，Walker通过对齿轮进行齿廓修形而避免了齿轮传动过程中的啮入啮出冲击。自此以后齿轮修形逐渐成为齿轮设计制造领域的热点问题，国内外学者和工程师针对齿轮的修形方式、方法进行了大量的理论与试验研究。Seire[2]通过齿轮副接触方程的求解得到了直齿圆柱齿轮不同修形量的理论计算方法。Wang[3]分别研究了齿轮副在未修形和齿廓修形下其啮合刚度的变化规律。Wu[4]运用有限元软件，构建齿轮传动系统的静态有限元接触模型和动态分析模型，对比了齿轮修形前后的力学特性和动态特性。Imerk[5]通过实验发现修形可使齿轮副的载荷分配更加均匀，并可以减少齿面的磨损，增加齿轮寿命。朱才朝[6]通过对含修形齿轮的行星齿轮箱进行振动测试，发现齿轮修形可使振动在啮合频率及其倍频处的幅值减小，使系统更加平稳。王成[7]基于非线性动力学理论构建了包含齿轮侧隙以及齿轮副非线性啮合刚度的横—扭—摆耦合非线性动力学模型，得到了不同修形量下齿轮副的振动幅值。

综合国内外关于齿轮修形的研究内容发现，利用动态传动误差评价修形齿轮的文章鲜有报道，而动态传动误差被认为是引起齿轮传动系统振动和噪声的主要激励源[8-9]。因此，本文基于动态传动误差对齿廓修形直齿轮进行了动态特性分析。

1 直齿轮副刚度及静态传动误差计算

1.1 目标齿轮副

本文研究的对象为两对直齿轮，其中一对未修形，另一对大轮、小轮均进行齿廓修形，修形量为10 μm，齿轮的具体参数见表1。图1为目标直齿轮副的三维模型。本文采用的直齿轮副全部通过齿面淬火磨削，保证齿廓修形后齿形精确。

表1 直齿轮副的几何参数

1.2 有限元接触模型

齿轮属于复杂曲面零件，不能直接使用软件中的结构化网格或者扫掠网格进行划分。因此，本文在对齿轮单齿划分网格前，先通过软件中的实体分割命令，将齿轮的单齿分成6块简单的六面体形状，如图2所示。齿轮单齿经过实体分割成6份后，每个部分都是一个变形的六面体，接下来对单齿进行六面体单元的结构化网格划分。单齿网格划分后的模型如图3所示。

完成单齿网格模型后，通过软件的装配模块，阵列得到直齿轮的多齿模型，为了节省计算时间，本文采用五齿模型开展直齿轮副的时变啮合刚度和静态传动误差的计算。图4为直齿轮副的有限元五齿模型。

1.3 时变啮合刚度和静态传动误差

考虑到有限元模型不可避免存在的由网格划分所带来的几何误差以及数值计算误差，为了消除这些误差对齿轮啮合刚度计算的影响，本文以大齿轮负载为1 Nm时的传动误差作为无负载传动误差，基于有限元计算结果可以计算出不同修形量下直齿轮在负载为150 Nm下的啮合力，如图5所示。静态传动误差如图6所示。直齿轮的啮合刚度km的计算公式为:

(1)

其中：Fn为啮合力；Rg为节圆半径；STE为含负载静态传动误差；NLTE为空载静态传动误差；X为动态传动误差。通过式(1)可计算出直齿轮的时变啮合刚度，如图7所示。

图1直齿轮副三维模型图2单齿的实体分割

从图5～图7可以得到以下结论：①与未修形齿轮副相比较，修形后静态传动误差和啮合刚度在单双齿交替啮合处的突变有所增大；②与未修形齿廓相比较，修形后直齿轮副的啮合周期并未发生改变，但单齿啮合区长度增加，双齿啮合区长度减小,这说明齿廓修形使直齿轮副的重合度减小，相同齿廓修形高度条件下，随着齿廓最大修形量的增加，重合度减小。

图3单齿结构化网格划分图4直齿轮五齿模型

2 直齿轮传动系统动力学模型

2.1 单级直齿轮传动系统动力学建模

根据转子动力学理论，直齿轮传动系统建模过程中可以将齿轮简化为转子，在高速旋转时，齿轮转子存在陀螺效应。与普通的转子不同，齿轮之间存在相互啮合作用，因而两个转子之间存在耦合作用，该耦合作用可以根据啮合法线方向的力的关系关联起来。同时，轴与轴承的弹性对高速圆柱齿轮传动系统的动态特性影响较大，且齿轮转子存在陀螺效应。本文将轴简化为Timoshenko梁单元，轴承简化为支撑刚度矩阵。根据文献[10]提出的有限元节点法，建立包含26个节点的齿轮—转子系统的动力学模型，图8为该系统的有限元节点模型。

图5两对直齿轮副啮合力图6静态传动误差图7两对直齿轮副时变啮合刚度

图8 直齿轮传动系统有限元节点模型

通过推导得出系统各成分(齿轮转子、柔性轴、轴承、啮合齿副)的动力学模型并得到相应的参数，根据有限元的思想，组合各个单元可以得到整个系统的运动方程为：

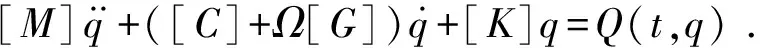
(2)

其中：[M]为质量矩阵；[C]为阻尼矩阵；Ω为轴的旋转速度；[G]为陀螺力矩阵；[K]为刚度矩阵；q为啮合线方向的相对位移；Q为齿轮传动系统的激励函数。动态各矩阵具体参数详见参考文献[10]。

2.2 动态传动误差分析

基于非线性振动理论，对上一节中构建的直齿轮副动力学模型求解，得到两对齿轮副在转速为6 000 r/min、载荷为150 Nm时的动态传动误差。由于传动误差高频成分反映齿轮传动系统的动态特性，因此对其进行高通滤波，得到的动态传动误差高频成分如图9所示，并对其进行傅里叶变换得到传动误差高频段频谱图，如图10所示。

通过图10可以看出，数值计算得到的动态传动误差高频段主要以啮合频率及其倍频成分为主，齿廓修形10 μm直齿轮副的0.5倍和1.5倍啮合频率成分被激励出来，但幅值很小，且修形10 μm齿轮副在啮合频率及其倍频处的频率成分幅值与未修形齿轮副相比有明显降低，即对直齿轮副进行合适修形量的齿廓修形可以减小齿轮传动系统的动态传动误差，改善系统的动态性能。

图9理论计算动态传动误差高频成分图10动态传动误差高频段频谱图

3 动态传动误差测试

3.1 测试系统构建

本次传动误差测试要求最高转速为6 000 r/min，根据齿轮副动态传动误差的测试要求和技术难点，决定采用磁栅作为转角传感器，采用LMS数据采集前端作为采集设备，构建的传动误差测试系统如图11所示。

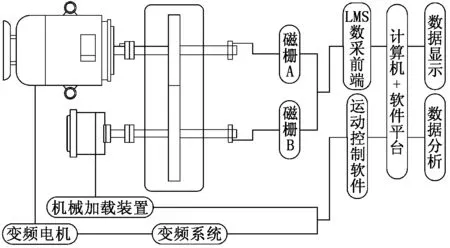
图11 动态传动误差测试系统

3.2 测试数据分析

利用传动误差测试系统进行直齿轮副动态传动误差测量，分别得到两对齿轮副在转速为6 000 r/min、载荷为150 Nm时的动态传动误差曲线，如图12所示。从图12中可以看出，齿轮副动态传动误差为近似正弦曲线，由低频成分和高频成分构成，其中低频成分对应于输入轴、输出轴的轴频及其倍频，高频成分为齿轮副的啮合频率及其倍频。对测得的动态传动误差数据进行高通滤波后进行傅里叶变换，得到传动误差高频段频谱图，图13为试验测得的动态传动误差在一倍啮合频率和二倍啮合频率处的频谱图。试验结果显示修形10 μm齿轮副在各啮合频率倍频处的幅值均小于未修形齿轮副，该结论与理论计算结果相同。

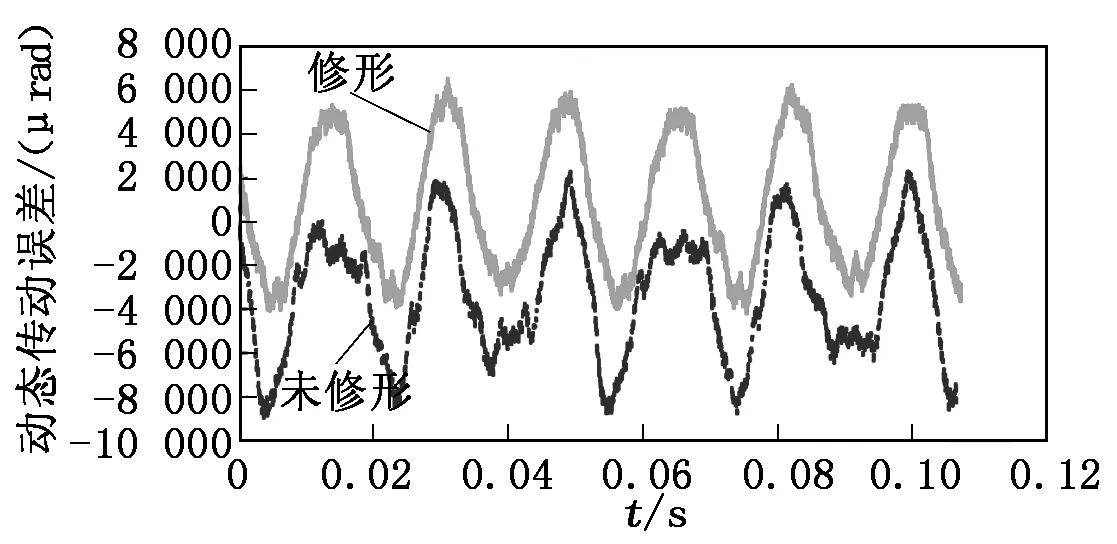
图12 试验测量得到的动态传动误差曲线

3.3 动态传动误差理论计算结果与试验数据对比

图14为未修形齿轮副动态传动误差高频段理论计算值与试验测试值的对比图。从图14中可以看出，传动误差的试验测试值比理论值略大，且试验测试值频率成分更为丰富，存在较多尖峰波动。这一现象的解释为，在对直齿轮传动系统进行动力学建模时，并未考虑齿轮的齿形误差，而将齿轮轮齿假设为具有理想渐开线的光滑齿廓，而在齿轮的实际加工过程中，存在齿形误差，会导致动态传动误差曲线出现尖峰波动。通过未修形齿轮副动态传动误差高频段理论计算值及试验测试值的对比，验证了直齿轮传动系统动力学模型的准确性。

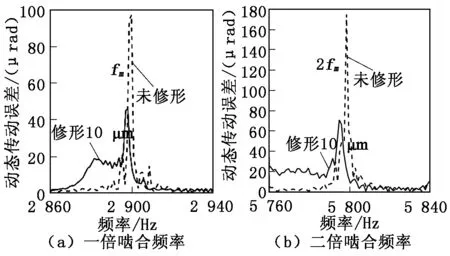
图13 动态传动误差高频段频谱图

图14 未修形齿轮副动态传动误差理论试验对比

4 结论

通过理论计算和试验测试方法对比未修形直齿轮副和齿廓修形直齿轮副的动态传动误差，发现修形直齿轮副的动态传动误差高频段各频率成分与未修形齿轮副相比均有明显降低，而齿轮传动系统动态传动误差高频的幅值决定了系统动态性能的优劣。因此，对直齿轮副进行合适修形量的齿廓修形可以减小系统的动态传动误差，改善系统的动态特性。

参考文献：

[1] Walker H.Gear tooth deflection and profile modification[J].Engineer,1938,166:434-436.

[2] Conry T F,Seireg A.A mathematical programming technique for evaluation of load distribution and optimum modification for gear system[J].Journal of Engineering for Industry,Trans ASME,1973:195.

[3] Howard I,Jia S X,Wang J.The dynamic modeling of a spurgear in mesh including friction and a crack[J].Mechanical Systems and Signal Processing,2001(5):831-851.

[4] Wu Y,Wang J,Han Q.Static/dynamic contact FEA and experimental study for tooth profile modification of helical gears[J].Journal of Mechanical Science and Technology,2012,26(5):1409-1417.

[5] Duzcuoglu I H H.Relation betwween wear and tooth width modification in spur gears[J].Wear,2007,262(3):390.

[6] 朱才朝,陈爽,马飞,等.轮齿修形对兆瓦级风电齿轮箱动态特性影响[J].振动与冲击,2013,32(7):123-128.

[7] 王成.渐开线直齿轮传动系统非线性动力学研究[D].北京:北京理工大学,2015:23.

[8] Munro R G,Palmer D.Gear transmission error outside the normal path of contact due to corner and top contact[J].Journal of Mechanical Engineering Science,1999,213:389-400.

[9] Chen S,Tang J,Wu L.Dynamics analysis of a crowned gear transmission system with impact damping:based on experimental transmission error[J].Mechanism and Machine Theory,2014,74(6):354-369.

[10] Hu Z,Tang J,Zhong J,et al.Frequency spectrum and vibration analysis of high speed gear-rotor system with tooth root crack considering transmission error excitation[J].Engineering Failure Analysis,2015:60.