谐波传动双圆弧共轭齿廓的优化设计

余金宝，范元勋

(南京理工大学 机械工程学院，南京 210094)

0 引言

谐波传动的双圆弧齿形是由Ishikawa提出[1]，这种齿形既可实现刚柔轮啮合区的持续接触，又增加了啮合齿对数[2]，降低了齿根处的应力同时提高了承载能力[3]，现已被广泛应用。在设计双圆弧柔轮和刚轮齿廓的过程中，应在保证柔轮具有高强度的条件下，先设计柔轮的凸齿廓和凹齿廓；再求出二者的理论共轭齿廓；最后调整柔轮的齿廓参数，使得柔轮齿廓与理论共轭齿廓的圆弧段共轭区域达到最大[4]。

本文从柔轮基本齿廓坐标系出发，用分段函数来表示柔轮齿廓，再代入共轭方程表达式求解柔轮的理论共轭齿廓，最后对柔轮的齿廓参数进行优化设计，使共轭区域最大化，提高双圆弧谐波传动的承载能力，为以后谐波齿轮传动的优化设计提供参考。

1 齿形建模

虽然刚柔轮在运动周期内某一时刻的啮合状态不同，但是啮合齿对在整个齿圈上的运动性质相同。因此可以将整个齿圈啮合齿的研究简化为某一个啮合齿对的研究[5]。

1.1 柔轮齿廓坐标系和参数模型

柔轮齿廓坐标系如图1所示。

图1 柔轮齿廓坐标系

由图得，齿廓坐标系xoy的x轴与齿根高线重合，y轴与齿廓的对称线重合，三条线段的坐标方程分别为[6]：

AB段凸圆弧齿廓坐标方程:

由柔轮齿厚与齿槽宽的比值(齿厚比K，通常取K=1)确定节线点M的位置，过M点作相对y轴逆时针旋转α角度的直线L1，过坐标原点作与x轴夹角为α的直线L2，两条直线相交于点B，则柔轮齿顶圆与凸圆弧段的交点及B点的坐标分别为：

(1)

(2)

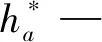
凸圆弧圆心O1坐标为：

(xo1,yo1)=(xj-Racosα,yj-Rasinα)

(3)

凸圆弧的坐标方程：

(4)

BC段切线齿廓坐标方程：

B、C点是关于M的对称点，坐标如下：

(5)

M点坐标已知，切线斜率已知，则直线段坐标方程为：

(6)

CD段凹圆弧齿廓坐标方程：

D点坐标为凹圆弧段与柔轮齿根圆的交点，坐标如下：

(7)

凹圆弧圆心O2坐标为：

(xo2,yo2)=(xC+Rfcosα,yC+Rfsinα)

(8)

凹圆弧齿廓坐标方程为：

(9)

1.2 共轭齿廓坐标系及表达式

描述刚柔轮相对位置的坐标系系统如图2所示。

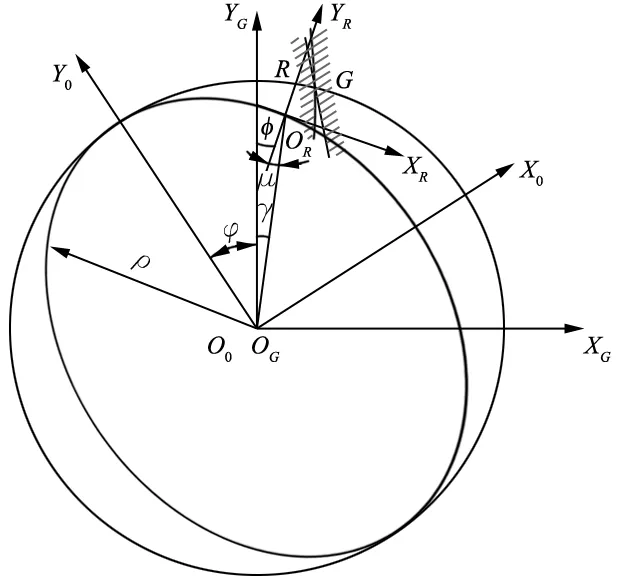
图2 刚柔轮相对位置坐标系

(xR,yR)为柔轮齿廓坐标系上的任意点，相对应的共轭齿廓上的点为(xG,yG)可按下式求得[7]：

(10)

变换矩阵相应的参数可由下式求出：

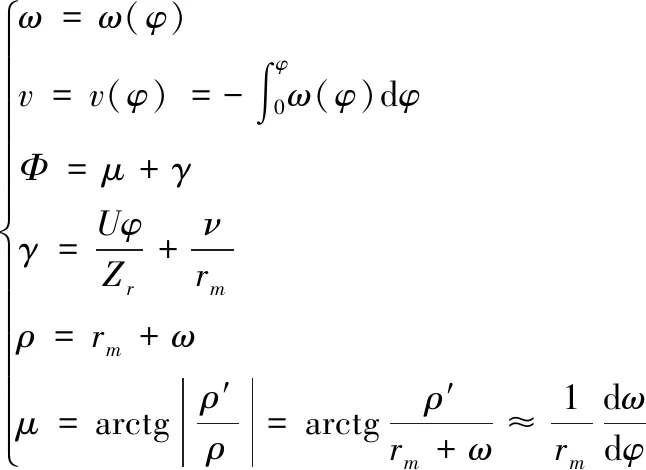
(11)

φ—波发生器转角；ω—柔轮中性线径向变形函数；ν—柔轮中性线切向变形函数；U—波发生器波数；Zr—柔轮齿数，U/Zr为广义传动比；rm—柔轮未变形前中性线半径；γ—柔轮转角；Φ—波发生器转动时，柔轮坐标系相对于刚轮坐标系的转动角度；ρ—柔轮变性后中性线的极半径；μ—波发生器转动时，柔轮轮齿偏转角度。

进行理论共轭齿廓求解时一般要作如下简化和假设[8]：

(1)柔轮的变形严格遵循理论变形曲线；

(2)柔轮中性线不随着柔轮的变形伸长；

(3)柔轮的齿形不会随着柔轮变形改变；

(4)柔轮变形后的理论截面依然是平面。

将柔轮的三段齿廓坐标方程式(4)、式(6)、式(9)和式(11)代入到式(10)中，共轭齿廓坐标方程由柔轮坐标系的x值和波发生器转角φ两个参数表示，包络条件方程表达式如下：

(12)

将柔轮的齿廓方程离散为n段，对于每一段i都相对应一个齿廓坐标参数x。根据式(12)，在波发生器转动的一个周期内，都有与x值对应的转角φ，φ值所构成的解集范围就是柔轮齿廓的共轭区间，对应的刚轮齿廓就是理论共轭齿廓。

2 齿形求解

本例波发生器采用双波传动，变形规律为余弦函数，模数m=0.45，全齿高h=1.8m，柔轮齿数Zr=160，刚轮齿数Zg=162，具体齿廓参数如表2所示。

表2 齿廓参数

利用上一章的共轭齿廓求解方法，得到的共轭区间及各段共轭齿廓如图3、图4所示。

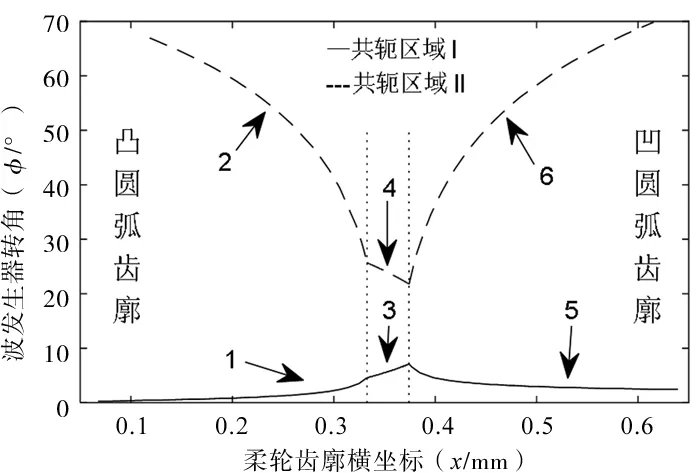
图3 共轭区域

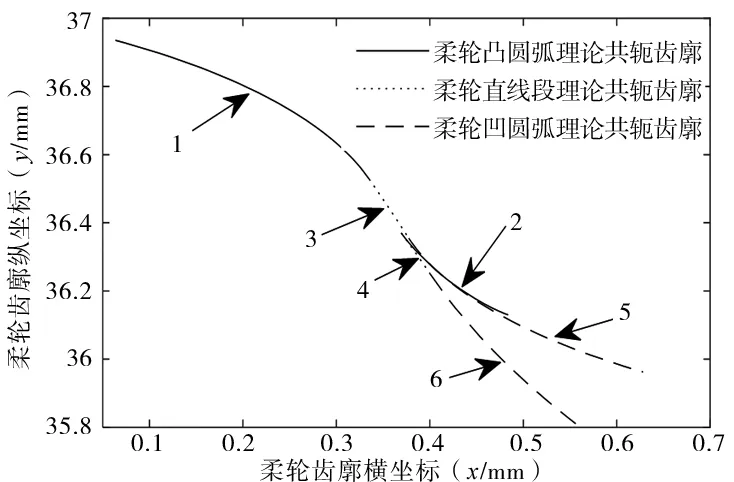
图4 理论共轭齿廓

由图3、图4可得，柔轮的三段齿廓分别对应两段理论共轭齿廓，凸圆弧齿廓对应1、2段理论共轭齿廓；直线段齿廓对应3、4段理论共轭齿廓；凹圆弧齿廓对应5、6段理论共轭齿廓。

刚轮的理论齿廓由分段理论共轭齿廓组成。根据图4，如果含有齿廓4、5、6，则会导致柔轮凸圆弧齿廓在与理论共轭齿廓2啮合时，发生啮合干涉，因此刚轮齿廓只能由齿廓1、3、2构成。所以，共轭关系只发生在图3中共轭区域I中的1、2段和共轭区域II中的3段，柔轮凸圆弧段齿廓发生两次共轭运动，直线段发生一次共轭运动，凹齿廓不发生共轭运动。

又由图4可以看出，齿廓2与齿廓5之间的差异很小，若使二者一致，刚轮齿廓包含理论共轭齿廓5，在整个啮合区域I内，柔轮的3段齿廓都会发生共轭运动并且会出现凹齿廓与直线段、凹齿廓与凸齿廓同时发生共轭运动的“双共轭”现象，这对提高谐波传动的承载能力有着重要作用[9]。本文提出一种优化方法来缩小2齿廓与5齿廓间的差异，使二者尽量一致，实现啮合区域内 “双共轭”区间的最大化。

3 齿廓参数优化设计

3.1 建立数学模型

齿廓2和齿廓5分别为两条线段，可以将其离散为n个点，通过对比各点的差异来衡量曲线的差异[10]。令两条曲线分别由函数s1(x)和s2(x)表示，基于离散点的齿廓函数向量表达式为：

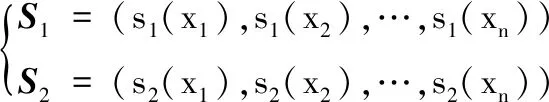
(13)

根据第一章的柔轮齿廓函数坐标方程，若保持柔轮齿廓直线段的齿廓方程不变，则函数值s1(xi)和s2(xi)只与凸圆弧半径Ra和凹圆弧半径Rf有关。令函数D(Ra,Rf)=‖S1-S2‖,即向量S1和S2的距离来表示2齿廓的一致性。齿廓2和齿廓5的向量长度不同，离散点x1，x2，···xn的取值范围应为二者的公共区域。

本次优化设计变量为柔轮齿廓凸圆弧半径Ra和凹圆弧半径Rf，取离散点的个数n=50，以函数D(Ra,Rf) 最小为目标，使齿廓2和齿廓5的一致性达到最佳。

3.2 单变量分析

先保证柔轮齿廓凸圆弧段半径Ra=0.72mm不变，改变凹圆弧段半径值Rf，研究Rf对齿廓2和5之间差异的影响。选取Rf∈[0.576,0.864]进行计算，计算结果如图5所示。

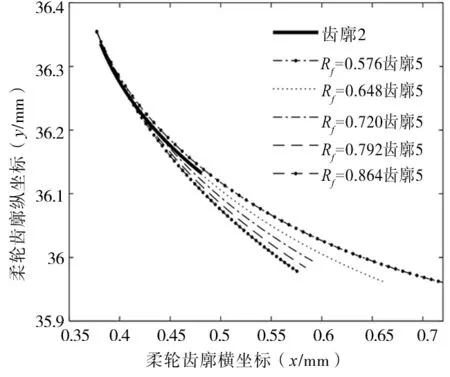
图5 不同Rf下的齿廓5

由图5可知，当凹圆弧齿廓半径Rf=0.648mm时，齿廓2和5差异最小，Rf大于0.648mm或者小于0.648mm时，二者差异增大，所以将Rf的计算区间缩小为[0.576,0.72]。2齿廓差异基于向量函数D(Rf)的变化规律如图6所示。

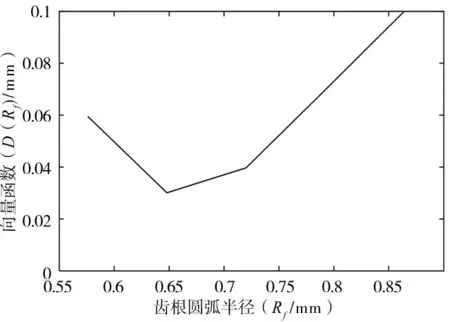
图6 函数D(Rf)变化规律

根据图6显示的函数D变化规律，在Rf=0.648mm时函数值为最小，大于或小于0.648mm时函数值增加，这与图5中的2和5齿廓差异变化规律相吻合。

研究凸齿廓圆弧半径对2齿廓差异的影响规律时，先取凹齿廓优化区间的临界值和中间值，即{0.576，0.648，0.72}，计算结果如图7所示。

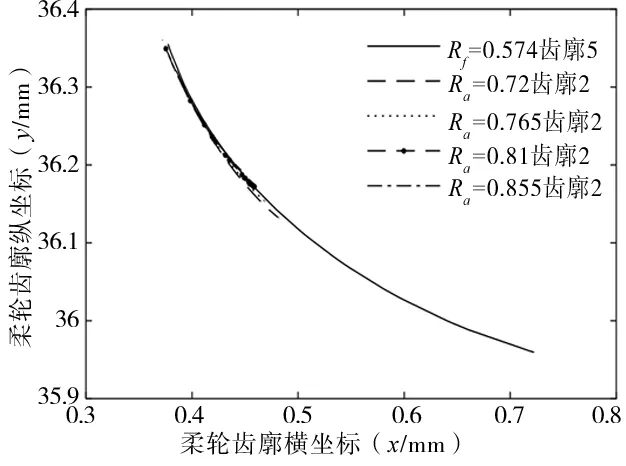
(a) Rf=0.564对应区间的齿廓2

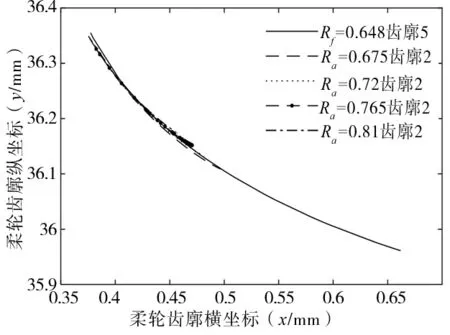
(b) Rf=0.648对应区间的齿廓2

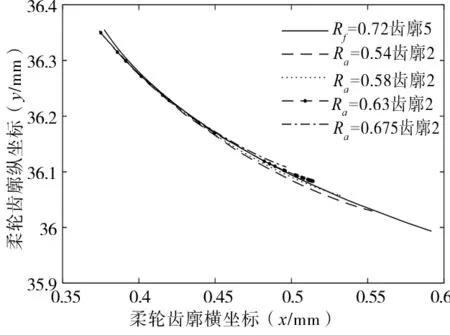
(c) Rf=0.72对应区间的齿廓2 图7 单参数变化的齿廓2曲线族

根据计算结果可以确定Rf=0.564mm时，凸齿廓半径的优化区间为[0.72,0.855]，同理，Rf=0.648mm和Rf=0.72mm对应的凸齿廓半径的优化区间为[0.675,0.81]和[0.54,0.675]，所以经计算后确定凸齿廓半径的优化区间为[0.54,0.855]。对函数D(Ra)在优化区间内进行更细化求解，以得到最优值，图8为在给定的3个凹齿廓半径下，函数D(Ra)在优化区间内随着Ra的变化曲线。

图8 函数D(Ra)的变化曲线

由图8可得，凹圆弧半径Rf=0.564mm、Rf=0.648mm和Rf=0.72mm时，在凸圆弧优化区间内，当Ra=0.765mm、Ra=0.81mm及Ra=0.63mm时，函数D(Ra)达到最小。因此，对于不同的凸齿廓和凹齿廓的半径组合，都能在所确定的优化区间内使函数D(Ra,Rf)达到最小。

根据以上的单变量分析可得，向量函数D(Ra,Rf)可以表征齿廓2和齿廓5之间的差异，衡量二者的一致性。在固定一个变量的情况下，可以通过改变另一变量使函数D达到最小，但是函数D的值往往是两个变量共同作用的结果。因此，需要进行多变量优化设计，使函数D(Ra,Rf)达到最优。

3.3 多变量优化设计

根据上一节确定的凸齿廓和凹齿廓的半径优化区间，将两个变量在各自的区间取11和15个离散值，计算D(Ra,Rf)在165对变量组合下的函数值，得到最优值如下：

Dmin(Ra,Rf)=D(0.6975,0.6768)=0.0238mm

在此最优值下，齿廓2和齿廓5的差异可由离散点s(xi)的平均差和最大差来衡量，具体如下：

max|s1(Δxi)-s2(Δxi)|=5.1×10-3mm

average|s1(Δxi)-s2(Δxi)|=2.99×10-3mm

在实际的工程应用中，此种精度下的齿廓可以认为一致。因此，本次多参数优化设计可以缩小齿廓2和齿廓5之间的差异，增大刚柔轮啮合时的“双共轭”区域，提高谐波齿轮传动的承载能力和传动精度。

4 结论

根据刚柔轮啮合时的运动规律及包络条件方程，进行柔轮齿廓的理论共轭齿廓求解，建立向量距离函数D(Ra,Rf)，研究结果表明该函数可以衡量两个齿廓的一致性。

进行目标函数D(Ra,Rf)的双参数优化设计，使函数D(Ra,Rf)最小，增大刚柔轮啮合时的“双共轭”区域，提高谐波传动的承载能力和刚度。

虽然改变凸齿廓和凹齿廓的半径参数可以使共轭区域增加，但是此种方法的工艺性有待进一步研究。