谐波齿轮传动柔轮的应力和疲劳强度分析*

王玉玲 张旭刚 张 华 江志刚

(①武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉430081；②武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉430081)

谐波减速机是一种高精密减速传动装置，由刚轮，柔轮和波发生器3个主要元件组成。它通过柔轮周期性的弹性变形和刚轮与柔轮的齿间啮合来传递运动和动力，具有体积小、传动比大和传动平稳等优点。柔轮作为谐波减速机的核心元件，其强度和寿命直接影响了整个谐波传动的可靠性和耐久性[1]。在交变载荷作用下，柔轮极易发生疲劳断裂[2]，严重影响了谐波传动的精度和效率。因此，对柔轮的应力和疲劳强度分析有助于提高谐波减速机工作性能和使用寿命

随着计算机性能的提升和有限元方法的发展，有了许多关于柔轮应力和疲劳强度的研究。文献[3]将柔轮轮齿简化为当量齿圈，利用有限元方法研究柔轮壁厚、筒长和齿宽对柔轮最大应力的影响。文献[4]建立了农业机器人转向机构的杯形柔轮有限元模型，并结合理论分析了柔轮空载下的应力分布状况。文献[5]建立了柔轮的实体模型并导入到ANSYS软件中对其进行寿命仿真和评估，没有给出柔轮疲劳强度的理论分析。以往关于柔轮有限元分析的研究，很少采用理论计算与仿真相结合的方法，也很少分析柔轮在不同负载下应力和疲劳安全系数分布规律。因此本文在Inventor中建立了未简化轮齿的杯型柔轮模型，以提高有限元的仿真精度。对柔轮有限元模型进行结构静力仿真，并结合理论计算，得到了柔轮负载下应力和位移的变化规律，在此基础上研究了柔轮负载时疲劳寿命，该结论对提高谐波减速机柔轮的工作寿命具有一定的参考价值。

1 柔轮应力分析

1.1 空载状态下柔轮应力分析

空载状态下柔轮的应力为预应力，是在装配时由于椭圆凸轮波发生器的作用而使柔轮变形时产生的[6]。这个变形力可以通过分析椭圆凸轮模型在长轴方向对柔轮产生的径向变形量来确定。本文根据文献[7]的柔轮计算模型，采用四力作用式凸轮波发生器，如图1所示。

由圆柱壳体理论有，柔轮在该波发生器作用下的径向变形为：

w=w0cos(2φ)

(1)

柔轮空载下沿轴线方向的弯曲应力为：

(2)

柔轮空载下沿周向弯曲应力为：

(3)

柔轮空载下扭转剪应力为：

(4)

式中：w0为柔轮最大径向变形量；s1为柔轮齿圈处壁厚；w为柔轮径向变形量；L为柔轮筒体长度；φ为以长轴为计算起点度量的角度；rm为轮中线的半径；E为弹性模量；v为泊松比。

本文以某型号谐波减速机为研究对象，其刚轮、柔轮、柔性轴承和波发生器的装配图如图2所示，柔轮相关参数为w0=0.372 mm,s1=1.376 mm,L=34 mm,rm=31.35 mm, 柔轮的材料选用40CrNiMoA,其弹性模量和泊松比分别为209 GPa和0.3。将柔轮的结构参数代入上述几个式子，可以解出柔轮空载下的最大应力值为166.98 MPa。

1.2 空载下柔轮应力有限元分析和验证

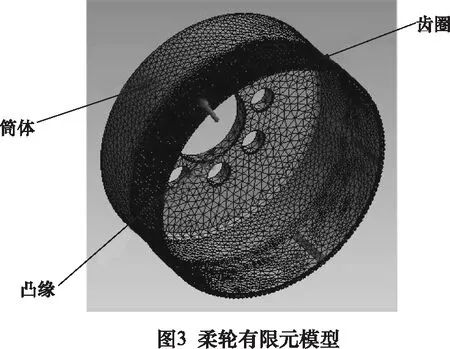
首先在Inventor软件中建立柔轮的三维模型，然后将其导人到ANSYS Workbench中。为了便于网格的划分和载荷的添加，将柔轮切分为4部分，分别是齿圈、筒体、筒体与凸缘过渡部分和筒体凸缘部分。在柔轮齿圈内侧划分出4个小矩形区域来施加相应压力。由于所选型号的谐波减速机中柔轮与箱体是靠螺栓连接的，因此将柔轮底部8个小圆柱面施加固定约束。柔轮有限元模型如图3所示。

对柔轮进行静力结构分析，得到柔轮的等效应力和位移云图如图4所示。从柔轮等效应力云图上可以看到柔轮受到波发生器的最大应力主要集中在齿圈中部(波发生器长轴作用区域)以及齿圈和筒体的过渡区域，且最大应力值为165.09 MPa，考虑到施加压力的过程中会造成一定的应力集中，所以去掉这个最大值，观察齿圈中部的应力主要集中在140～165 MPa，这与之前理论计算得到的166.98 MPa相比，误差不是很大，说明柔轮应力的仿真结果符合实际情况。从柔轮的变形云图中可以看到柔轮最大变形量为0.373 96 mm，而此型号的柔轮径向最大变形0.372 mm。

1.3 负载下柔轮应力和变形规律

为了得到柔轮疲劳强度与负载的关系以及确定柔轮的工作负荷，本文研究了柔轮在不同扭矩作用下的应力和位移变化情况。柔轮在负载时与刚轮啮合，主要受到凸轮对柔轮的变形力和刚轮轮齿产生的扭矩。柔轮负载下的边界约束与空载状态下有一定的不同。本文采用文献[8]的方法，在波发生器长轴方向上的两个相对应轮齿节圆上的若干节点上施加切向力以模拟柔轮轮齿所受到刚轮轮齿产生的扭矩，切向力与所施加扭矩有以下关系：

(5)

式中：M为施加的扭矩，R为柔轮的节圆半径，N为柔轮轮齿节圆上所施加切向力的节点数。

本文N=11，选取7组不同的扭矩值。由式(5)，扭矩值和施加的切向力的数值如表1所示。

表1 柔轮轮齿上的载荷换算

当柔轮受到负载时,对其进行静力结构分析，可以得到不同扭矩下柔轮的应力和变形云图。图5显示了T=60 N·m作用下的有限元分析云图。

从图中可以看到，柔轮应力和变形云图形状并没有发生较大的改变，但是柔轮的最大等效应力和最大变形量都增加了，此外筒体和凸缘的连接部分也出现了一定的应力集中。为了更清晰地呈现柔轮最大等效应力和位移随负载分布状况，将7种扭矩作用下的柔轮最大等效应力云图和柔轮在齿圈和筒体过渡处(即轴向长度x=13.67 mm)的变形云图分别绘制成曲线图，如图6所示。

图6a显示，随着扭矩的增大，柔轮最大等效应力值也在不断增大，在空载到负载100 N·m的时候，应力的增值比较平稳，而在100 N·m 之后，最大应力值快速增长。因此对于柔轮材料为40CrNiMoA，模数是0.39 mm，筒体壁厚为0.6 mm的柔轮在100 N·m以下为最佳工作载荷段。

图6b显示，柔轮的最大变形是呈谐波形状的，且为对称分布，柔轮的最大位移出现在周向长度为30 mm、80 mm、130 mm和180 mm附近，分别对应着柔轮长轴即凸轮波发生器作用位置和柔轮短轴处。其次在柔轮受到的扭矩较小时即T=20 N·m时，其变形曲线与扭矩较大时相比偏移了一个相位角。随着扭矩的逐渐增大，柔轮最大位移值每次只增长大约0.1 mm，柔轮筒体变形云图的颜色分布没有发生明显的改变，说明负载的变化对柔轮变形规律没有太大影响，柔轮最大径向变形取决于波发生器的轮廓形状。

2 柔轮疲劳分析

2.1 柔轮疲劳强度理论

柔轮是谐波减速机中最关键也是最易受损的零件，在交变载荷下，柔轮易发生疲劳断裂。因此柔轮的疲劳强度分析对提高谐波减速机的传动精度具有重要的意义。本文先采用理论计算的方法求出柔轮在负载T=100 N·m时的安全因子，然后再对其进行疲劳寿命的有限元仿真以验证理论结果的可靠性。

柔轮沿轴线方向的正应力、周向正应力和变形产生的剪应力分别为[5]：

(6)

(7)

(8)

令扭矩为T，则作用于柔轮上的切应力为：

(9)

采用双向稳定变应力状态下的安全系数来校验柔轮的疲劳强度。

只有切应力作用时柔轮的安全系数为：

(10)

只有正应力作用时柔轮的安全系数为：

(11)

正应力和切应力同时作用时的柔轮疲劳安全系数可以表示为：

(12)

表2 Cσ、C与β的取值

因为柔轮的疲劳安全系数不应小于1.5，上式计算的柔轮在负载T=100 N·m时的安全系数是1.607>1.5,说明柔轮符合疲劳强度要求。

2.2 柔轮疲劳有限元分析

为了验证柔轮在负载T=100 N·m时疲劳强度计算结果的可靠性，在有限元软件中插入疲劳工具，输入柔轮材料的S-N曲线即交变应力幅值与工作循环次数曲线。设置载荷类型为Fully Reversed，最终可得到柔轮在扭矩T=100 N·m下的疲劳寿命云图和安全系数云图，如图7所示。柔轮在此工作状态下疲劳寿命为106次，最小疲劳安全因子为1.615 4，主要位置是柔轮齿圈、柔轮齿圈与筒体过渡处和筒体与凸缘过渡处，与理论计算值1.607的误差为0.46%，说明理论计算的结果可靠。

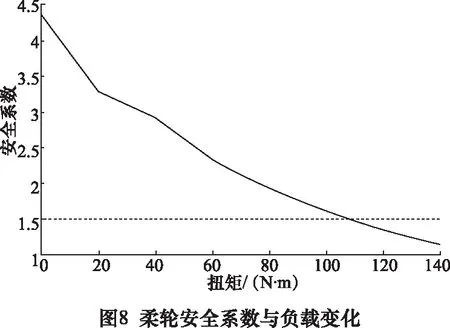
将柔轮在不同负载下的安全系数绘制成曲线如图8所示，可知在扭矩T≥110 N·m时柔轮易发生疲劳失效。

3 结语

本文利用Inventor软件和ANSYS Workbench仿真软件对谐波减速机的柔轮进行了应力和疲劳分析，并结合圆柱壳体理论和疲劳强度理论验证了分析结果的可靠性。通过分析柔轮在空载和负载状态下的应力和变形规律，得到如下结论：

(1)柔轮最大变形量集中在柔轮长轴和短轴区域，在负载较小时，此变形规律会偏移一个相位角。

(2) 柔轮最大等效应力集中在齿圈位置，齿圈与筒体过渡位置和凸缘与筒体的过渡位置。

(3)扭矩的增大对柔轮最大位移影响不大，柔轮的最大径向位移是由凸轮波发生器决定的，而最大应力值随着负载的增大而增大，且柔轮的最佳工作载荷范围是T≤100 N·m。

(4)柔轮的疲劳系数随负载的增大而迅速降低，在扭矩T=110 N·m左右时，柔轮易发生疲劳断裂。该研究方法和结论能为柔轮结构设计，应力分析和疲劳优化提供一定的理论和技术支持。