圆柱杯形柔轮的应力变形分析*

□ 邱 吉 □ 柳 丽 □ 李国平 □ 刘锦扬 □ 罗利敏 □ 贡林欢

1宁波大学 浙江省零件轧制与成型技术重点实验室 浙江宁波 315211 2宁波中大力德智能传动股份有限公司 浙江宁波 315301

1 分析背景

谐波传动通过机械波迫使挠性构件产生谐波运动,从而完成运动传递。谐波传动装置主要由刚轮、柔轮、波发生器等组成[1]。谐波传动具有传动比大、体积小、精度高等特点,广泛应用于机器人、航空航天、光学仪器等领域[2-3]。谐波传动中,柔轮承受的应力、变形比较复杂,且在实际工作中,柔轮较其它零件更易产生破坏。因此,延长柔轮的疲劳寿命一直是谐波减速器需要解决的主要问题[4-5]。

国内外许多学者对柔轮进行了大量理论分析与研究。邓一波等[6]通过建立柔轮和刚轮、波发生器之间的接触模型,得到装配时的柔轮应力分布云图及负载时的柔轮应力变化曲线。邢静忠等[7]利用柔轮的参数化模型,分别计算了柔轮在装配状态和负载工况下的最大应力及分布规律,并研究了长径比、膜板宽度等几何参数对柔轮筒底最大装配应力和负载应力的影响规律。韦乐余[8]通过正交设计法,对柔轮长度、齿圈厚度等主要结构参数进行组合,分析疲劳寿命,提取各结构参数下柔轮的最大等效应力和疲劳循环次数拟合曲线,从而得到各结构参数对柔轮应力和疲劳寿命的影响规律。

笔者针对某工程中应用的XB1单级谐波传动圆柱杯形柔轮,进行不同厚径比和不同长度两种组别建模,并进行有限元分析,得到圆柱杯形柔轮应力和变形规律,对圆柱杯形柔轮结构参数进行优化改进。所做分析可以降低柔轮最大应力,减小变形,延长疲劳寿命,提高谐波传动精度,具有一定的工程应用价值。

2 三维简化建模

直接建立柔轮的力学模型并不简单,许多学者在做分析之前都会对模型进行简化。阳培等[9]对柔轮轮齿进行简化,将轮齿部分抹平,简化为当量光滑圆柱壳体,由此柔轮变为光滑变厚度的薄壁壳。同时将波发生器看作理想刚性体,在与柔轮配合时不发生任何变形,认为柔轮的法兰部分是刚性的,柔轮模型为对称模型。王天赐[10]在对柔轮进行分析时,为方便设置载荷和计算,忽略齿圈与筒体的过渡圆弧半径、齿廓曲线中的齿根圆角。

由于笔者的分析与齿轮啮合没有关系,并且研究的是柔轮空载下的应力与变形,不存在扭矩,因此在建立模型时忽略法兰部分的螺纹孔,并对柔轮的轮齿部分进行抹平,形成光滑的当量齿圈。

某工程中应用的XB1单级谐波传动圆柱杯形柔轮截面示意图如图1所示。原始柔轮内壁半径d为25 mm,柔轮长度L为48 mm,模数为0.4 mm。根据经验公式计算柔轮其它结构参数,并在Pro/E软件中进行参数化三维建模,如图2所示。波发生器一般作为输入端,使柔轮产生连续变形。笔者选取标准椭圆曲线凸轮波发生器,根据经验公式计算并绘制其外椭圆表面轮廓,厚度为9 mm。建立的波发生器三维模型如图3所示。

▲图1 柔轮截面

根据有限元分析需要,在建立实体模型时,需要建立一个原始模型及两个系列的圆柱杯形柔轮实体模型。对于原始模型,设置其筒体壁厚为0.5 mm,长度为48 mm,内径为50 mm。对于不同厚径比模型,在其它参数不变的情况下,只改变筒体壁厚。柔轮厚径比为0.005～0.030,每隔0.005增加一组参数模型,共设置六组模型进行对比。对于不同长度模型,在其它参数不变的情况下,只改变长度。柔轮长度为32～60 mm,每隔4 mm增加一组参数模型,共设置八组模型进行对比。

3 有限元建模

将建立好的各个实体模型导入ANSYS Workbeneh软件,进行有限元分析。定义圆柱杯形柔轮的材料为35CrMnSiA,弹性模量为210 GPa,泊松比为0.3,实体单元选择SOLID185单元。为提高分析精度,在划分网格前,先对实体模型进行分割,取1/4模型进行分析,如图4所示。

▲图2 柔轮三维模型 ▲图3 波发生器三维模型

▲图4 柔轮1/4模型

网格划分时,不同面所需要的单元密集程度不同,规定除筒体外径面单元尺寸为1 mm外,其余单元尺寸为0.5 mm。柔轮网格划分模型如图5所示,共有14 694个节点、14 801个单元。

▲图5 柔轮网格划分模型

定义接触时,由于波发生器的刚度比圆柱杯形柔轮的刚度大得多,因此笔者假定波发生器为刚体,在传动时不发生变形,柔轮为柔体。分析时将波发生器设定为刚性,定义接触面为柔轮的内表面,选用CONTACT174单元。波发生器的外表面为目标面,选用TARGET170单元,设置摩擦因数为0.15。

由于柔轮的法兰被固定在减速箱上,因此将法兰内侧的位移自由度全部约束。波发生器为刚体,将波发生器内表面的位移自由度全部约束,并对柔轮的两边施加位移对称约束。对分析类型、时间、步长等进行设置,即可进行求解。

4 厚径比影响分析

根据谐波减速器的实际工作要求,对圆柱杯形柔轮的有限元分析主要关注应力及变形。在保证其它参数不变的情况下,只改变柔轮的厚径比,通过已经建立的模型进行有限元分析,当厚径比为0.005、0.015、0.030时,柔轮应力、变形云图分别如图6、图7所示。不同厚径比时柔轮最大应力和变形变化规律如图8所示。

▲图6 不同厚径比时柔轮应力云图

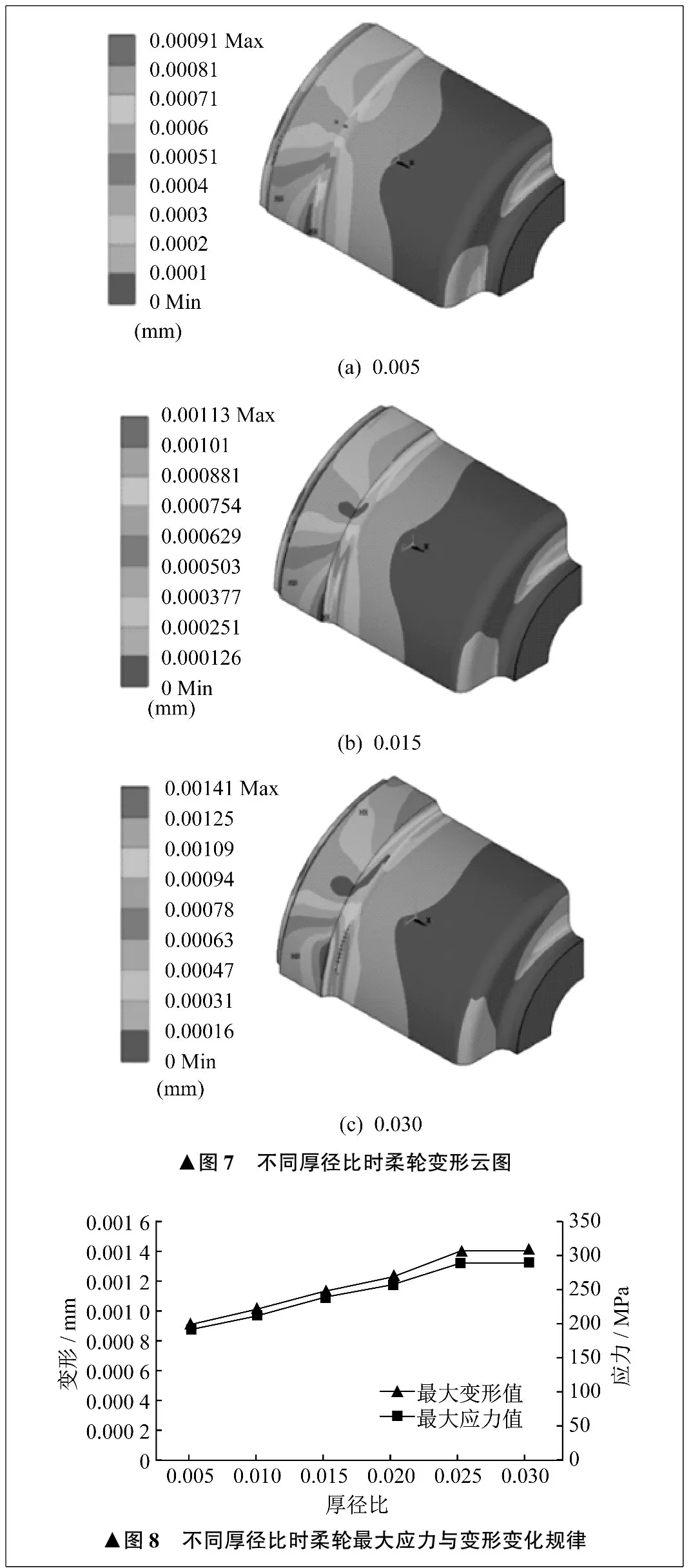
▲图7 不同厚径比时柔轮变形云图▲图8 不同厚径比时柔轮最大应力与变形变化规律

圆柱杯形柔轮厚径比为0.015时,最大变形值为0.001 13 mm。减小柔轮的齿圈壁厚,柔轮的最大变形值也随之减小,并且趋势很明显。厚径比从0.015减小到0.005,柔轮最大变形值从0.001 13 mm减小到0.000 91 mm,为原始模型的80.5%。当厚径比从0.015增大到0.025时,柔轮的最大变形值从0.001 13 mm增大到0.001 39 mm,为原始模型的123%。厚径比从0.025增大到0.030,柔轮最大变形值增大了0.000 02 mm,增大值很小。当厚径比从0.005增大到0.025时,柔轮最大变形值基本呈线性增大。厚径比为0.030的柔轮,在齿圈与筒体的过渡区域有不连续的痕迹,说明不能继续增大齿圈厚度,否则柔轮存在破裂的可能性。

当柔轮的厚径比从0.015减小到0.005时,最大应力值从237.664 MPa减小到190.593 MPa,降为原始模型的80.2%。当柔轮的厚径比从0.015增大到0.025时,柔轮的最大应力值从237.664 MPa增大到287.524 MPa,为原始模型的121%。厚径比从0.005增大到0.025,柔轮的最大应力值基本呈线性变化增大。当厚径比增大到0.030时,有限元模型出现断裂,其最大应力值相比厚径比为0.025时仅增大了2.56 MPa。通过应力云图可知,柔轮最大应力集中在齿圈与筒体接近的地方。

综合以上分析,可以得到以下结论:增大齿圈厚度,柔轮的应力与变形均相应增大;减小齿圈厚度,柔轮的应力与变形均相应减小。但一味减小齿圈厚度,会加大柔轮的加工难度。增大齿圈厚度,则会导致柔轮出现断裂。因此,柔轮的厚径比在0.10～0.20之间最为合适。在对不同长度柔轮进行应力与变形分析时,选用厚径比为0.015的柔轮模型。

5 长度影响分析

圆柱杯形柔轮厚径比为0.015,在其它参数不变的条件下,只改变柔轮的长度,对八个模型进行有限元分析。当柔轮长度为32 mm、40 mm、60 mm时,应力与变形云图分别如图9、图10所示。不同长度时柔轮最大应力和变形变化规律如图11所示。

长度在40～52 mm区间时,柔轮最大变形值随长度的增大逐渐减小。长度达到52 mm后,柔轮最大变形值趋于平稳。长度从40 mm减小到32 mm时,柔轮最大变形值突然增大。由此可知,增大长度可以减小柔轮最大变形值,延长寿命;减小长度会增大最大变形值,缩短寿命。

长度增大时,柔轮最大应力值减小。长度由48 mm增大到60 mm,柔轮最大应力值减小30 MPa。长度减小时,柔轮最大应力值增大。长度由48 mm减小到40 mm,柔轮最大应力值增大33.846 MPa。长度由40 mm减小到32 mm,柔轮最大应力值增大103.275 MPa,增大趋势较为明显。当长度为32 mm时,柔轮最大应力集中在波发生器长轴方向柔轮的齿圈及齿圈与柔轮过渡的区域。随着长度的增大,在齿圈及齿圈与柔轮过渡圆角处,应力集中现象减弱。当长度增大到60 mm后,应力集中只存在于波发生器短轴方向柔轮筒底与凸台的过渡圆角处,以及波发生器长轴方向柔轮筒底与凸台的过渡圆角处。

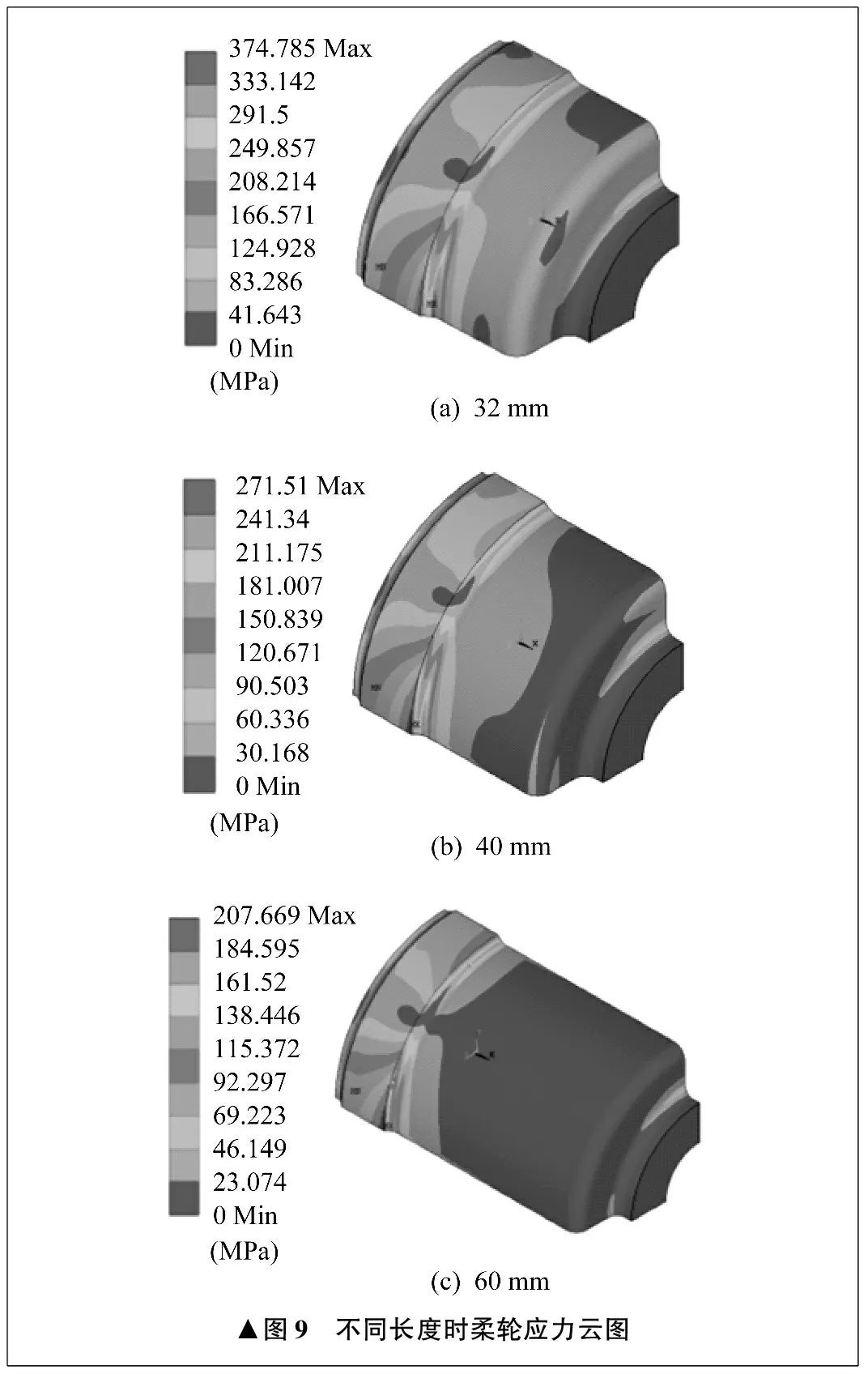
▲图9 不同长度时柔轮应力云图

综合以上分析可见,厚径比为0.015时,柔轮的长度为40～52 mm比较合适。

6 结束语

笔者通过设置主要参数厚径比与长度,对圆柱杯形柔轮进行简化建模、有限元分析,对数据进行对比,得出研究区间内柔轮的最大应力和变形随厚径比的增大而增大,随长度的增大而减小。长度对柔轮应力与变形的影响比厚径比更大,在满足强度及传动性能的前提下,应尽量减小长度,以使谐波传动装置的体积小,质量轻。综合两方面分析,对选取的工程案例进行参数优化,确认柔轮的最佳厚径比为0.015,最佳长度为40 mm。

▲图10 不同长度时柔轮变形云图

▲图11 不同长度时柔轮最大应力与变形变化规律