剪张型微地震震源机制与振幅分布特征

唐 杰 王 浩 温 雷 张文征(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580；②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071)

1 引言

水力压裂是页岩气增产的主要手段，是用高压泵组将流体注入页岩层产生剪张裂隙[1]。产生裂隙的过程中可以诱发微地震事件，通过对微地震事件的观测、处理，能够分析水力压裂的影响、效果及地下应力状态等[2]。研究微地震的震源机制能够获得岩石破裂面方向、倾角等信息以及破裂面的张裂和剪切滑动等属性，为水力压裂复杂裂缝网络解释提供依据。

Gilbert[3]首次引入矩张量研究震源机制。震源矩张量是源张量和介质参数的复合效应，震源区的各向异性使震源特征变得复杂，微地震震源中的非双力偶成分与介质各向异性有关，采用各向同性介质进行反演时可能会产生虚假的非双力偶成分[4]。蔡晓刚等[5]研究了各向异性ATI介质中的剪切位错源地震矩张量，结果表明即使剪切位错源在各向异性介质中仍能产生非双力偶分量。近年来许多学者针对由地震波形资料反演地震矩张量做了大量的研究[6]，微地震震源机制反演方法主要分为两大类：基于井中观测数据的和基于地表观测数据的震源机制反演方法。井中观测数据由于观测方位不足及观测噪声的影响，反演精度受限；地表监测的微地震数据，信噪比通常较低，需要首先采取措施压制噪声干扰，再进行微地震定位和震源机制反演[7]。有研究发现水力压裂诱发的微地震事件中有很多为非双力偶类型，表明岩石可能发生了剪张破裂，与剪切型震源相比，拉张型震源在震源特征上表现出很多的差异，如剪张型震源频谱的高频部分会迅速衰减，而剪切型震源频谱更宽，衰减更慢[8]； 此外二者的双力偶成分百分比和振幅特征也有差异。Pesicek等[9]采用密集地表地震数据证实了水压裂所导致微地震中包含非双力偶机制；Foulger等[10]分析了便携式地震记录仪记录的数据，通过P波、S波极性和振幅比反演获得了微地震的震源机制，结果表明震源类型为剪切和拉张断裂的组合； Walter等[11]建立了拉张型破裂远区震源谱模型，并与剪切型地震远区模型进行对比，发现拉张型破裂的P/S波振幅比异常高； Eaton等[12]的研究表明大约90%的剪切型事件的S/P波振幅比大于5，而拉张型事件的S/P波振幅比均小于4.671，因而可通过S/P波振幅比确定震源类型。

本文研究了微地震剪张源震源机制，分析了剪张源微地震信号的辐射花样和能量传播特征，通过数值计算获得了地表接收的不同震相的振幅分布。

2 剪张源模型与震源表示方法

2.1 剪张源的源张量与矩张量

震源机制是指震源区在地震发生时的力学过程，微地震的震源破裂包含剪切滑动成分和张裂(或压裂)成分(图1)。当然在实际的地质条件下，水力压裂导致的破裂面滑动方向会受到压裂液、该区域的主应力方向及周围的断层裂隙等因素的影响[13]。

假定断层面法向n=(n1,n2,n3)T、位错方向v=(v1,v2,v3)T，与走向角φ、倾角ψ、滑动角θ和张裂角α(图1)的关系[14]为

(1)

(2)

φ、ψ、θ和α通常是空间位置和时间的函数，为了简化忽略其时空变化，与研究剪张错动的点源相似。φ、ψ和θ描述了断层面的法向和沿着断层面位错矢量的切向，而α描述了偏离断层面的位错矢量的偏离程度。α的范围为[-90°，90°]，当α>0°时表示剪张源；对于纯张裂源，α=90°；α<0°代表压裂源；对于纯压裂源，α=-90°；对于纯剪切源，α=0°。

剪张源的源张量D满足

(3)

式中：u是位错矢量的大小；S为断面面积；uS表示震源强度。

对于各向同性介质，矩张量M和源张量D之间满足[15]

Mij=λDkkδij+2μDij

(4)

式中：λ和μ是拉梅常数；δ是克罗内克函数；i、j和k可取的值为1、2和3，式(4)采用爱因斯坦求和约定，在同一项中，如果同一指标(如式中的k)成对出现，就表示遍历其取值范围求和。由于任意地震的矩张量必须满足净应力和净应力矩均为零的基本条件，因此矩张量M中的元素满足Mij=Mji，即M是一个对称矩阵，只有6个独立的元素。

2.2 震源各分量随张裂角α的变化

微地震震源矩张量M釆用特征值分解法可以分解为双力偶部分(DC)、补偿线性矢量极偶成分(CLVD)以及各向同性部分(ISO)[16]，即

M=MISO+MCLVD+MDC

(5)

式中

(6)

(7)

(8)

ISO成分和CLVD成分之和被称为非DC成分，CLVD和DC成分被称为矩张量偏量部分M*，参数ε是CLVD相对于DC成分的大小[16]，定义为

(9)

(10)

式中κ=λ/μ。

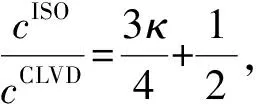
图2 ISO、CLVD和DC成分随张裂角α的变化(a)泊松比σ=0.15； (b)泊松比σ=0.25

3 剪张源辐射花样与能量传播特征

3.1 剪张源辐射花样

若以到原点的距离长短表示震源球面上地震波振幅的强弱，则可构成地震波的辐射花样。震源机制与地震波场函数之间的关系可以表示为[18]

(11)

(12)

剪张源的P波和S波的三维辐射花样随着张裂角的变化如图3所示。P波辐射花样中纯压裂源(α=-90°)和纯张裂源(α=90°)包含两个波瓣，而剪张源(90°>α>0°)有四个波瓣，在纯剪切源(α=0°)中，P波的辐射花样中包含两个节面，其中一个为断层面，另一个为辅助面，S波则没有节面；而在纯张裂源(α=90°)中，P波没有节面且极性为正，P波和S波辐射花样是轴对称的[18]。

3.2 剪张源辐射能量随张裂角的变化

剪张型震源的S波和P波辐射能量比满足[19]

(13)

图4a为剪张源的P波辐射系数RP随张裂角的变化，可以看出，随着张裂角的增大，P波辐射系数先减小再急剧增加；图4b为剪张源的S波辐射系数RS随张裂角的变化，可以看出，随着张裂角的增大，S波和SH波均方根辐射系数先减小再急剧增加，而SV波的均方根辐射系数先减小再少量增加，张裂角小于特定值之前，SV波均方根辐射系数大于SH波，超过这个角度，SV波均方根辐射系数大于SH波；图4c为剪张源的横波能量与纵波能量比值随张裂角的变化，可以看出当张裂角较小时，横波辐射能量较大，而当张裂角较大时，横波辐射能量较小，随着张裂角的增大，该比值先有所增加后急剧减小。

图3 剪张源的P波(上)和S波(下)的辐射花样随着张裂角的变化

图4 剪张源辐射能量随张裂角的变化(a)P波辐射系数； (b)S波辐射系数； (c)平均横波能量/平均纵波能量

4 剪张型微地震振幅分布特征

4.1 矩张量分布和震源机制沙滩球

矩张量分解可以采用不同的方式[20]，如Hudson分解[21]、Bi-Axes分解[22]、Tape分解[23]等，同样可以采用Hudson图[21]、钻石图、Riedesel-Jordan图[24]、Bi-Axes图[22]及Lune图[23]等进行矩张量分析。

(14)

(15)

通过参数化运算，可以将矩张量的6个独立元素简化为两个元素(T、K)，其中T为张性组分，K为剪切组分，分别为

(16)

(17)

Hudson图中横坐标表示剪切组分T值，纵坐标表示张性组分K值，T、K的取值范围均为[-1，1]。图5a给出了泊松比σ=0.25和σ=0.35、不同张裂角α(90°、50°、10°、0°、-10°、-50°、-90°)震源的Hudson图分布，震源参数满足走向角φ=45°、倾角ψ=50°和滑动角θ=-40°。由图可知，不同的张裂角和泊松比会导致震源机制在Hudson图中的位置不同，图中各向同性爆炸型震源张量(ISO)中的膨胀震源(E)和压缩震源(I)的T-K坐标分别为(0，1)和(0，-1)； 当α=90°时，不同泊松比条件下的震源都为纯张裂源； 当α=0°时，不同泊松比条件下的震源都为纯剪切源，T-K坐标为(0，0)，位于Hudson图示的中心位置； 两类错动方向相反的补偿线性偶极子震源(CLVD(+)与 CLVD(-))的T-K坐标则分别为(-1，0)和(1，0)；当α=±10°和α=±50°时，震源为剪张型混合源，不同泊松比条件下的震源矩张量在Hudson图中的位置不同，随着张裂角绝对值的增大，剪切组分会减少。

此外还可以采用矩张量钻石图研究矩张量中ISO、DC和CLVD分量的分布情况[25]，如图5b所示。由图可知，相同的泊松比不同张裂角对应震源机制中CLVD和ISO的比是相同的；不同的泊松比对应震源机制中CLVD和ISO的比是不同的；相同的张裂角，泊松比较大的ISO/CLVD值也更大；随着张裂角的变化，DC和非DC分量的比例会发生变化。

图6给出了震源机制沙滩图随张裂角(α分别为90°、50°、10°、0°、-10°、-50°、-90°)的变化，其中P轴位于膨胀波象限，而T轴位于压缩波象限。由于剪张源中包含非DC分量，采用标准沙滩球表示剪张源不是十分合适，DC节线(图中蓝色线)并不对应断层的方向和位错面的方向。对于剪张源可以采用源节线来代替DC节线，即采用剪张源的走向角φ、倾角ψ和滑动角θ给出源节线(图中红色线)。

图5 不同张裂角(90°、50°、10°、0°、-10°、-50°、-90°)震源的Hudson图分布(a)和钻石图分布(b)

图6 震源机制沙滩球随张裂角的变化

由图6可知，当α为零时，震源为纯DC源，DC节线与源节线重合，而张裂角不为零时，DC节线与源节线之间存在偏差。由于节线与P波极性分布之间存在偏差，所以对于剪张源而言只采用P波极性反演矩张量很难获得较好的效果。此外，比较图6上与图6下可知，介质泊松比不同，震源机制沙滩球也不同。

4.2 地表接收信号振幅的分布特征

对于不同位置的微地震震源和检波器，可以采用射线追踪方法计算获得离源角和方位角，然后结合震源机制辐射花样可获得不同检波器位置不同震相的振幅值，获得的振幅值包含了辐射花样和传播路径的效应。首先选择泊松比σ=0.25的均匀介质，震源位于(0，0，1500m)处，震源走向角φ=45°、 倾角ψ=50°和滑动角θ=-40°，张裂角α分别取90°、10°和0°。检波器位于地表，图7～图9给出了P波、S波、SV波和SH波的各分量的总振幅以及垂直分量振幅，由图可知地面接收到的信号振幅分布与震源机制和检波器位置等有关，如果考虑噪声的影响，当震相对应的振幅较小时易被噪声所掩盖，采用该震相反演震源机制时就会出现较大误差。

4.3 波场快照

利用有限差分方法可以研究微地震信号的传播[26]，为了减小数值频散、满足稳定条件和提高计算效率，网格和时间参数都要随频率改变，其中模型网格间距Δh和时间增量Δt应满足

图7 α=90°时P波、S波、SH波和SV波的总振幅分布(上)及其垂直分量振幅分布(下)

图8 α=10°时P波、S波、SH波和SV波的总振幅分布(上)及其垂直分量振幅分布(下)

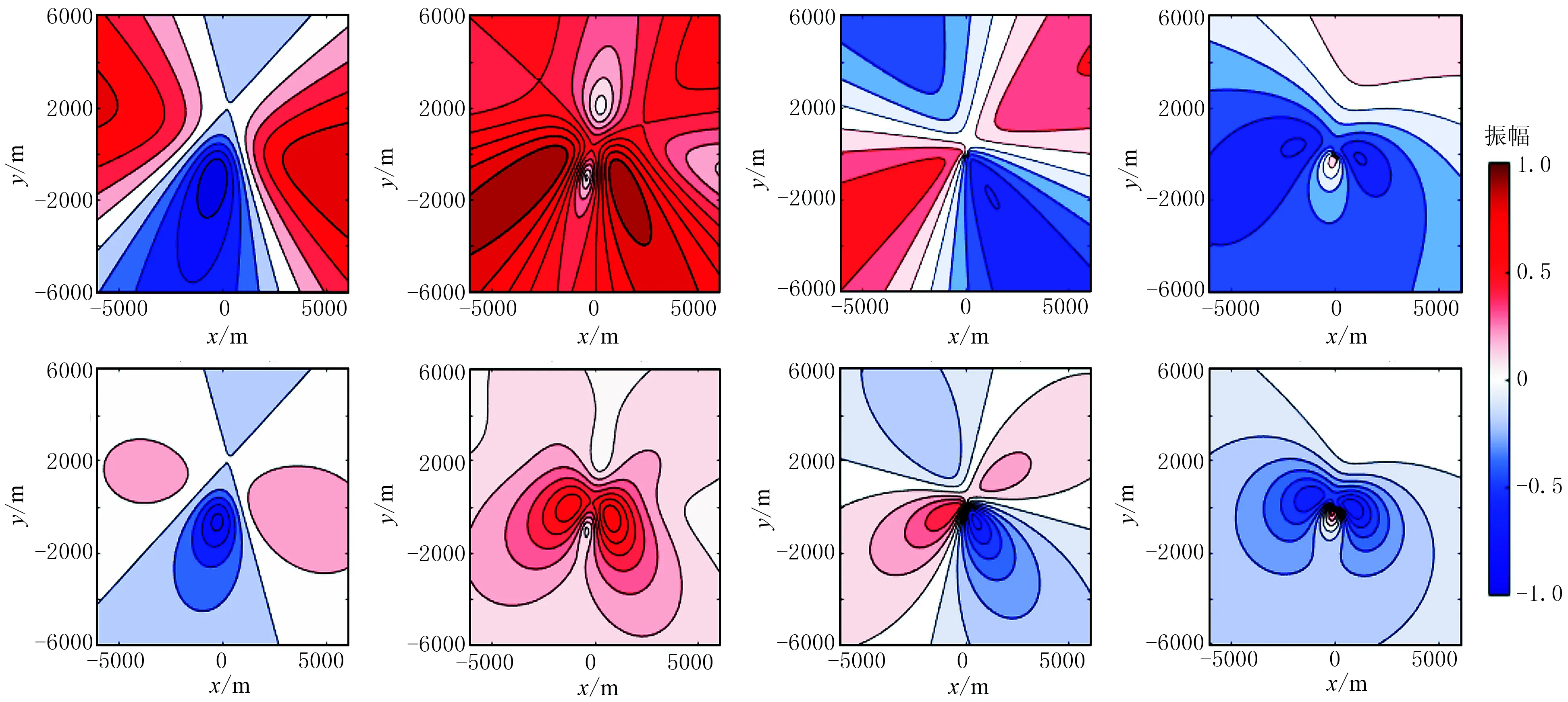
图9 α=0°时P波、S波、SH波和SV波的总振幅分布(上)及其垂直分量振幅分布(下)

(18)

式中Vmax为最大波速。

设计一个三维介质的微地震模型，模型的网格点数为100×100×100，空间采样间隔为5m×5m×5m，震源函数为Ricker子波，主频为30Hz，时间采样间隔为0.5ms，震源位于模型中心(250m，250m，250m)。图10～图12为100ms不同张裂角张裂源波场x、y和z分量在距地面100m深度处的xy平面的快照对比，由图可见，当张裂角度发生变化，x、y和z分量的极性和大小都可能发生变化，所以张裂角会明显地影响接收到微地震信号各分量的极性和大小。

图10 100ms不同张裂角张裂源波场x分量快照(a)α=90°； (b)α=10°； (c)α=0°

图11 100ms不同张裂角张裂源波场y分量快照(a)α=90°； (b)α=10°； (c)α=0°

图12 100ms不同张裂角张裂源波场z分量快照(a)α=90°； (b)α=10°； (c)α=0°

5 结论

本文研究了剪张源微地震震源机制，分析了剪张源微地震信号的辐射花样、能量传播特征以及地表接收到的不同震相的振幅分布，得到的主要结论如下。

(1)剪张源被认为是解释水力压裂诱发微地震震源机制较为合理的模型，该模型采用走向角、倾角、滑动角和张裂角表示其源张量，再结合介质参数即可得到震源矩张量。矩张量中各成分百分比可采用Hudson图和钻石图进行描述。

(2)通过理论研究及数值模拟发现ISO、CLVD和DC成分的百分比与张裂角的大小有关，例如当α=±90°时DC分量为零，当α=0°时DC分量为100%。另外，对于各向同性介质，在泊松比不变的情况下不同张裂角对应震源机制中CLVD与ISO的比是相同的。

(3)微地震震源辐射能量会随张裂角而发生变化，当张裂角较小时，平均横波能量较大，而当张裂角较大时，平均横波能量较小。

(4)地面接收到的信号振幅分布与震源机制、模型参数和检波器位置等有关，根据微地震事件的理论分析和数值模拟结果，可以更清楚地认识微地震的信号特征，从而指导地面压裂监测观测系统的设计。

参考文献

[1] 姚振岸，孙成禹，谢俊法等.黏弹TTI介质旋转交错网格微地震波场模拟.石油地球物理勘探，2017，52(2)：253-263.

Yao Zhenan，Sun Chengyu，Xie Junfa et al.Micro-seismic forward modeling in visco-elastic TTI media based on rotated staggered grid finite-difference me-thod.OGP，2017，52(2)：253-263.

[2] 方兵，孙成禹，唐杰等.微地震信号频率特性分析.石油地球物理勘探，2015，50(3)：411-417.

Fang Bing，Sun Chengyu，Tang Jie et al.Analysis of frequency characteristics of micro-seismic signals.OGP，2015，50(3)：411-417.

[3] Gilbert F.Excitation of the normal modes of the Earth by earthquake sources.Geophysics Journal of the Royal Astronomical Society，1971，22(2)：223-226.

[4] 张云银，刘海宁，李红梅等.应用微地震监测数据估算储层压裂改造体积.石油地球物理勘探，2017，52(2)：309-314.

Zhang Yunyin，Liu Haining，Li Hongmei et al.Reservoir fracturing volume estimation with micro-seismic monitoring data.OGP，2017，52(2)：309-314.

[5] 蔡晓刚，姚陈，陈晓非.各向异性ATI介质剪切位错源地震矩张量.地球物理学报，2011，54(7)：1772-1782.

Cai Xiaogang，Yao Chen，Chen Xiaofei.Seismic moment tensor in anisotropic ATI media：shear faulting.Chinese Journal of Geophysics，2011，54(7)：1772-1782.

[6] 曹俊海，顾汉明，尚新民.基于局部相关谱约束的多道匹配追踪算法识别微地震信号.石油地球物理勘探，2017，52(4)：704-714.

Cao Junhai，Gu Hanming，Shang Xinmin.Microseismic signal identification with multichannel matching pursuit based on local coherence spectrum constraint.OGP，2017，52(4)：704-714.

[7] 杨心超，朱海波，李宏等.基于P波辐射花样的压裂微地震震源机制反演方法研究及应用.石油物探，2016，55(5)：640-648.

Yang Xinchao，Zhu Haibo，Li Hong et al.Microseismic focal mechanism inversion based on P-wave radiation pattern and its application.GPP，2016，55(5)：640-648.

[8] 容娇君，李彦鹏，徐刚等.微地震裂缝检测技术应用实例.石油地球物理勘探，2015，50(5)：919-924.

Rong Jiaojun，Li Yanpeng，Xu Gang et al.Fracture detection with microseismic.OGP,2015,50(5):919-924.

[10] Foulger G R，Julian B R，Hill D P et al.Non-double-couple microearthquakes at Long Valley caldera，California，provide evidence for hydraulic fracturing.Journal of Volcanology & Geothermal Research，2004，132(1)：45-71.

[11] Walter W R，Brune J N.Spectra of seismic radiation from a tensile crack.Journal of Geophysical Research，1993，98(3)：4449-4459.

[12] Eaton D W，Forouhideh F.Solid angles and the impact of receiver-array geometry on microseismic moment-tensor inversion.Geophysics，2011，76(6)：75-83.

[16] Shimizu H，Sadato U，Koyama J.A tensile-shear crack model for the mechanism of volcanic earthquakes.Tectonophysics，1987，144(1-3)：287-300.

[18] Grzegorz K，Yehuda B.Assessment of P and S wave energy radiated from very small shear-tensile seismic events in a deep South African mine.Journal of Geophysical Research，2013，118(7)：3630-3641.

[19] Randall M J.The spectral theory of seismic sources.Bulletin of the Seismological Society of America，1973，63(3)：1133-1144.

Journal of Seismology，2015，19(1)：231-252.

[21] Hudson J A，Pearce R G，Rogers R M.Source type plot for inversion of the moment tensor.Journal of Geophysical Research Atmospheres，1989，94(B1)：765-774.

[22] Chapman C H and Leaney W S.A new moment-tensor decomposition for seismic events in anisotropic media.Geophysical Journal International，2011，188(1)：343-370.

[23] Tape W and Tape C.A geometric setting for moment tensors.Geophysical Journal International，2012，190(1)：476-498.

[24] Riedesel M A and Jordan T H.Display and assessment of seismic moment tensors.Bulletin of the Seismological Society of America，1989，79(1)：85-100.

[25] 姚振岸，孙成禹，唐杰等.基于不同震源机制的黏弹各向异性微地震波场模拟.石油地球物理勘探，2017，52(1)：63-70.

Yao Zhenan，Sun Chengyu，Tang Jie et al.Micro-seismic forward modeling in viscoelastic anisotropic media based on different focal mechanisms.OGP，2017，52(1)：63-70.

[26] 唐杰，方兵，孙成禹等.压裂诱发的微地震震源机制及信号传播特性研究.石油地球物理勘探，2015，50(4)：643-649.

Tang Jie，Fang Bing，Sun Chengyu et al.Study on focal mechanism of micro-seismic induced by hydrofracture and signal propagation characteristics.OGP，2015，50(4)：643-649.