基于角度滤波成像的最小二乘逆时偏移

刘梦丽 黄建平* 李 闯 崔 超 任英俊(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580；②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071)

1 引言

近年来，地震勘探对构造成像精度的要求越来越高，传统的偏移方法如Kirchhoff偏移、相移法等难以对横向速度变化剧烈的复杂构造准确成像。逆时偏移(RTM)对各种地震波型(一次波、多次波)和高陡构造成像具有明显优势[1]。成像条件是影响逆时偏移成像效果的主要因素，目前基于波场零延迟互相关成像条件得到广泛使用[2]，但是该条件忽略了地震波场的多路径和方向性特征。因此RTM直接使用该条件时会不可避免地引入低波数强振幅噪声，在浅层尤为明显[3-5]。业界为解决这一问题提出了许多方法，其中高通滤波是一种常用的去噪方法,但忽略了波场的多路径特点，造成有效反射信号被破坏[6]。Guitton等[7]在系统对比导数滤波与拉普拉斯滤波方法的基础上提出了最小平方滤波方法，在去噪的同时也能保存有效信息。此外，低频成像噪声主要由强反射界面反射波引起，在计算区域的噪声位置采用方向衰减的边界条件，利用无反射方程也能抑制噪声[8]。

在成像过程中消除噪声的思路成为业界关注的热点问题。坡印廷矢量去噪方法首先由坡印廷矢量的定义得到波场传播方向，然后对成像条件参数乘以一个方向衰减因子进行去噪，不但需要额外计算和存储波场传播矢量，而且在波场复杂区域提取的波场传播方向误差较大[9]； 此外，通过把波场分解为(波数域)上、下、左、右行波，运用成像条件时只保留方向相反的波场分量成像结果，这种方法可以有效去噪，但波场分解增加了额外计算量，且分解三维波场可能会损失有效信息[10]。Rocha[11]发展了能量范数成像条件，把成像条件看作震源波场与检波点波场之间的内积，可压制常规互相关造成的低频噪声。OP’t Root等[12]、Whitmore等[13]、Kiyashchenko等[14]根据Stolk提出的逆散射理论，结合入射波和反射波的时间导数成像条件和空间梯度成像条件压制低频噪声。

20世纪80年代，Tarantola[15]首先提出构建最小二乘的误差泛函方法求解反演问题。Nemeth等[16]首先使用Kirchhoff最小二乘偏移(LSM)方法对不规则反射地震数据进行偏移。LSM将偏移成像看作是最小二乘反演框架下的反演问题，能够克服常规RTM对储层成像分辨率不高且振幅不均衡等问题，且能在一定程度上消除偏移假象[17-21]。因此，人们将RTM与LSM的优势相结合发展了最小二乘逆时偏移(LSRTM)进行复杂构造的保幅成像处理[22,23]。针对LSRTM计算成本高的问题，基于编码策略的叠前平面波LSM成像能极大地提高计算效率[24,25]。

本文在前人研究的基础上，首先分析了RTM中低频噪声产生的原因，提出了一种满足能量守恒的逆散射成像条件，并与LSRTM结合，实现了基于角度滤波成像的最小二乘逆时偏移算法(ALSRTM)。最后，通过对SEG/EAGE二维盐丘模型的成像测试验证了ALSRTM 的有效性，并对比、分析了常规LSRTM及ALSRTM对低信噪比炮数据、含误差速度场的适应性。

2 ALSRTM

2.1 基于互相关成像条件的常规RTM

RTM通常分为震源波场正向延拓、记录波场逆时传播和互相关成像三部分。其中时间域的正传和反传过程通过对双程波波动方程

(1)

进行差分求解得到。式中：P(x,t,xs)为震源波场；Q(x,t,xr)为检波点波场；fs(xs,t)为震源函数；dobs(xs,xr,t)为检波点xr处在时刻t采集到的震源点xs处的地震记录；v(x)为地震波在介质中的传播速度。

应用传统的互相关成像条件可得偏移剖面

(2)

图1为低频噪声成像机制示意图。采用式(2)进行互相关成像条件的前提假设是：炮点上行波和检波点下行波场(图1中虚线)为零，仅仅利用炮点下行波和检波点上行波(图1中实线)信息进行互相关并成像，可得到理想的反射层成像结果。根据地震反射机理，若存在强反射界面，由于RTM以双程波波动方程为理论基础，震源波场在波阻抗界面处必然产生上行反射波，类似地，检波点波场在逆时延拓时也必然产生下行反射波，即同时存在炮点上行波场和检波点逆时延拓过程中的下行波场，在满足ts+tr等于地震道走时的位置均可成像，其成像结果为构造假象，严重影响成像精度。

图1 低频噪声成像机制示意图

式(2)代表的成像过程把波场看作标量，仅仅利用波场的数值成像，没有区分波场方向，因此成像结果中包含炮点上行波场和检波点逆时延拓过程中的下行波场造成的低频噪声。另外，从低频噪声成像机制示意图(图1)可以看出，在反射点(图1中的位置1)处的反射角较小，而在产生低频噪声的位置(图1中的位置2)震源波场方向与检波点波场方向之间的角度接近180°。

2.2 角度滤波成像条件

对于单个震源，局部震源波场P(x,t)和检波点波场Q(x,t)的射线参数分别为[13,26]

(4)

(5)

化简可得

(6)

(7)

由式(7)得到的偏移剖面相当于从成像结果中去除了反射角为θa对应的成像值。由低频噪声成像机制示意图(图1)可见，在低频噪声产生位置(图1中的位置2)的反射角θ大多在接近90°的大角度范围内，而在反射层成像位置(图1中的位置1)的反射角较小。对于正向传播的震源波场和反向传播的检波点波场来说，两者夹角主要集中在较小的区间内，在此区间内成像能突出有效波的能量；在低频噪声产生位置的反射角θ大多在接近90°的大角度范围内，则近似认为仅产生噪声，因此在此区间内的互相关不参与成像过程。因此，与坡印廷矢量成像去除低频噪声的思想类似，仅在θ较大的区间进行互相关(文中为了节省计算量，近似认为θ为90°)。

对比式(2)与式(7)可见：传统互相关成像条件(式(2))只包含了波场的数值大小，刻画了主要构造信息；能量成像条件(式(7))是波场的空间梯度和时间导数的线性叠加，速度是连接时间导数与空间梯度的“桥梁”，作为加权项作用于空间梯度，波场的局部时间导数则蕴含着波场的动力学特征(波形、振幅、频率、相位)以及地下地层结构、岩石结构及流体性质之间的关系，可使成像过程更准确。

为了验证新成像条件(式(7))的可靠性，从能量守恒的角度出发，定义各向同性介质声波方程的能量为[27]

(8)

(9)

(10)

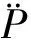
2.3 照明补偿预条件算子

由于常规偏移算子仅为正演算子的转置而不是逆，在成像时会受到地表观测系统的影响，造成对地下构造的不均匀照明，尤其是深部及高速盐体之下的构造，由于照明太弱而无法成像。因此，为了对深部构造更好地照明，本文使用炮照明算子进行补偿，该算子在时间域可表示为[6]

(12)

2.4 基于逆散射能量保幅成像条件的LSRTM

为了得到与记录数据最佳匹配的偏移结果，把LSRTM引入反演，其误差函数定义为

(13)

式中：L为Born近似下的反偏移算子；m为偏移剖面；d为观测数据。求解式(13)，第k次迭代得到的梯度为

gk=LT[Lmk-1-d]

(14)

本文利用共轭梯度法迭代求解式(13)，得到模拟数据与观测数据差别最小的最佳反射系数模型，迭代过程使成像结果具有更高的分辨率和更可靠的振幅保真度。实现流程如下：

(1)输入初始模型m0(对m0赋值0，即第一次迭代结果为逆时偏移剖面)、观测数据dobs、梯度误差阈值δ；

(2)计算第k次迭代的梯度gk、共轭方向修正因子β和共轭梯度zk

(3)计算步长α并对成像结果进行更新，得到

(4)判断是否满足终止迭代条件，若满足则退出并保存成像结果，否则退回到步骤(2)、步骤(3)继续迭代，直到满足迭代终止条件，最后一次迭代即为最终的成像结果。

3 模型试算

为了分析ALSRTM与LSRTM的地震成像效果，对SEG/EAGE二维盐丘模型(图2)进行成像测试。模型主要包括盐上沉积层、盐丘及盐下构造。主要考察ALSRTM成像算法对盐丘侧翼高陡小构造、盐上小断裂带及盐下小断裂带的成像效果，其中盐丘侧翼的高陡小构造会引起严重的构造假象， 而且由于盐丘的屏蔽作用，导致盐下构造的振幅较弱，难以准确成像[28]。稀疏采样引起成像结果中出现严重的偏移假象，因此能更好地测试、对比常规LSRTM和ALSRTM去除浅层低频噪声的效果。图3为RTM成像结果。由图可见：在拉普拉斯滤波前，RTM剖面中含有较强的低波数噪声和震源效应，难以识别地下构造(图3a)； 在拉普拉斯滤波后，在模型浅部仍然存在低频噪声和顶部的震源效应，成像能量不均衡、成像精度低，仍然难以识别盐下构造，但成像效果好于未做拉普拉斯滤波的RTM结果(图3b)。图4为LSRTM和ALSRTM成像结果对比。由图可见： ①当迭代5次时，在常规LSRTM成像结果中，盐上沉积层存在明显的偏移假象(图4a)； ALSRTM能较彻底、有效地压制低频噪声，且震源采集效应更弱，另外，对于盐丘上部小断裂的成像分辨率更高(图4b)。②当迭代10次时，常规LSRTM和ALSRTM均有效压制了低频噪声，采集脚印减弱，成像效果明显改善(图4c、图4d)，但常规LSRTM成像结果的浅层仍然存在较严重的噪声(图4c)； 值得注意的是，ALSRTM仅仅迭代5次时的成像结果(图4b)对噪声和采集脚印的压制效果甚至优于LSRTM迭代10次(图4c)的结果。③当迭代30次时，常规LSRTM和ALSRTM均能有效压制盐上沉积层的成像噪声，也能准确识别岩下构造(图4e、图4f)。

图2 SEG/EAGE二维盐丘模型(a)真实速度场； (b)平滑速度场； (c)反射率模型

图3 RTM成像结果(a)拉普拉斯滤波前； (b)拉普拉斯滤波后

震源是主频为20Hz的雷克子波，时间采样间隔为0.5ms，时间采样点数为4001； 总炮数为30炮，共645道检波器接收，炮间距为215m，道间距为10m

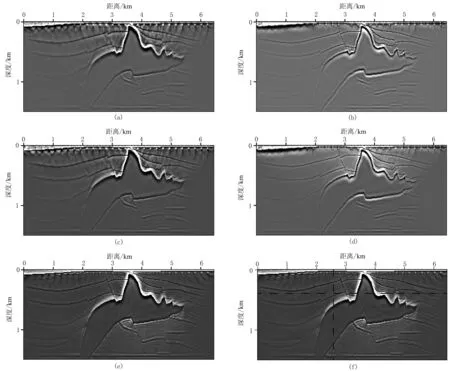
图4 LSRTM与ALSRTM成像结果对比(a)LSRTM迭代5次；(b)ALSRTM迭代5次；(c)LSRTM迭代10次；(d)ALSRTM迭代10次；(e)LSRTM迭代30次；(f)ALSRTM迭代30次

为了更清楚地对比常规LSRTM与ALSRTM方法的成像效果，从LSRTM和ALSRTM成像结果(图4)中截取浅层断块区域(深度范围为200～800m，水平范围为2000～5400m)的局部放大图进行对比(图5)。可见：在常规LSRTM成像剖面上盐上小断层的接触关系模糊，分辨率较低，当迭代5、10次时未能有效去除盐丘左侧之上和盐上反射层之间的低频假象(图5a、图5c黑色箭头所示)； 应用ALSRTM后(图5b、图5d、图5f)，盐上断层更为清晰，而且仅仅在迭代5次时，就可彻底压制盐丘左侧侧翼之上和盐上反射层之间的噪声(图5b)。

从LSRTM以及ALSRTM 的成像结果中分别抽取水平坐标2700m和深度400m处(图4f中虚线位置)的地震单道振幅(图6)对比各方法的保幅性(迭代30次)。可见：①在水平坐标2700m处，在模型的浅部区域由于存在低频噪声，常规LSRTM的振幅曲线存在明显跳动，而ALSRTM振幅曲线抖动幅度较小，与真实反射系数振幅曲线吻合更好(图6a的箭头所示)；在中深部ALSRTM 与常规LSRTM的保幅性几乎相同，两者的振幅曲线均较好地接近真实反射系数振幅曲线(图6a的*所示)。②截取盐丘正上方低频噪声严重区域在深度400m处的振幅曲线(图6b)可见，在模型的水平坐标2800、3400、4500m(被低频噪声严重干扰的反射界面)处，常规LSRTM振幅曲线与真实反射系数振幅曲线差距较大，而ALSRTM振幅曲线更接近真实反射系数振幅曲线(图6b的箭头所示)；在没有反射界面的位置，ALSRTM振幅曲线较常规LSRTM振幅曲线抖动小，抗噪性更好(图6b的*所示)。因此在浅层，ALSRTM比常规LSRTM具有更好的保幅性，尤其在低频噪声存在的位置，ALSRTM的优势更为明显，在中深层两者的振幅曲线均更接近于真实反射系数振幅曲线。

图7为ALSRTM、常规LSRTM成像结果的残差随迭代次数变化图。由图可见：①ALSRTM在第3次和第6次迭代时出现残差突然上升趋势(图7的黑色箭头所示)；②在第7次迭代之后，随着迭代次数增加，两种方法的残差都逐渐减小，在13次迭代之后，ALSRTM的残差略微小于常规LSRTM，两种方法的成像结果都逐渐趋近于真实模型；③随着迭代次数的增加，两种方法残差的减小速度逐渐减慢。需要说明的是，第3次和第6次成像时使用式(7)，其余迭代过程均使用式(2)，式(2)是在反偏移算子和偏移算子互为共轭转置的前提下得到的，因此数据残差稳定收敛，而式(7)是基于波场的动力学特征，在第3次和第6次迭代时不满足反偏移算子和偏移算子互为共轭转置的关系而出现抖动。为了测试ALSRTM和LSRTM对速度场的敏感性，在速度场中加入2%的误差后进行成像测试。 图8为加入2%速度误差的成像结果。 由图可见：随着迭代次数增加，ALSRTM(图8b、图8d、图8f)和LSRTM成像结果(图8a、图8c、图8e)均能清晰展现浅、中、深层构造，但前者的偏移假象更少、成像精度更高。因此，ALSRTM对速度场求取不准具有更好的适应性。

图5 图4的局部放大(a)LSRTM迭代5次；(b)ALSRTM迭代5次；(c)LSRTM迭代10次；(d)ALSRTM迭代10次；(e)LSRTM迭代30次；(f)ALSRTM迭代30次

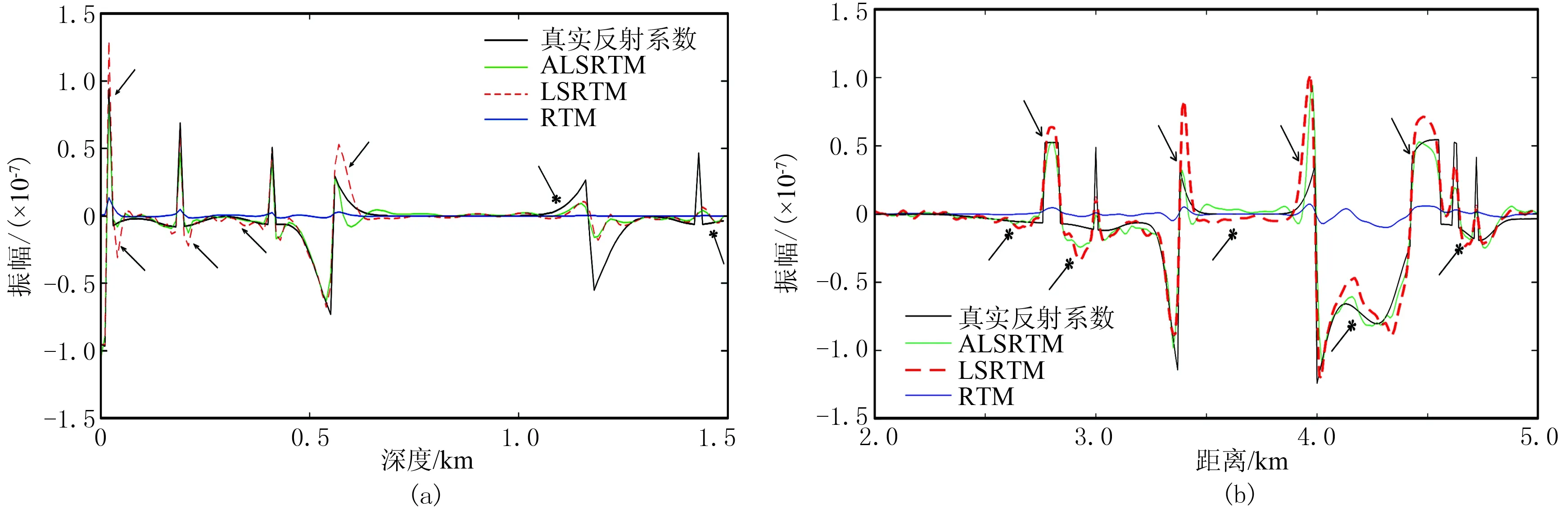
图6 成像结果单道振幅对比(迭代30次)(a)水平坐标2700m处； (b)深度坐标400m处

图7 ALSRTM、常规LSRTM成像结果的残差随迭代次数变化(迭代60次)

图8 加入2%速度误差的成像结果(a)LSRTM迭代5次；(b)ALSRTM迭代5次；(c)LSRTM迭代10次；(d)ALSRTM迭代10次；(e)LSRTM迭代30次；(f)ALSRTM迭代30次

野外地震采集数据中不可避免地含有环境及人文因素造成的随机噪声。为了测试ALSRTM对低信噪比数据的适应性，通过 Madagascar软件对炮记录添加随机噪声得到低信噪比单炮数据(图9)。图10为低信噪比数据成像结果。由图可见：对于低信噪比数据，LSRTM(图10a、图10b)和ALSRTM成像结果(图10c、图10d)都含有类似于随机噪声的偏移假象，但后者更好地压制了低频噪声。因此，ALSRTM对低信噪比炮记录的适应性更好。

图9 低信噪比单炮数据

图10 低信噪比数据成像结果(a)LSRTM迭代5次； (b)LSRTM迭代10次； (c)ALSRTM迭代5次； (d)ALSRTM迭代10次

4 结束语

通过波场数据得到的反射角信息构建逆散射成像条件，并与最小二乘逆时偏移(LSRTM)结合，发展了一种基于角度滤波成像的最小二乘逆时偏移方法(ALSRTM)，并由波动方程的能量守恒分析了ALSRTM的可行性和保幅性。在实现算法的基础上，对SEG/EAGE二维盐丘模型的稀疏采集地震数据的成像结果表明，ALSRTM在改善常规LSRTM的成像质量及保幅性方面是有效的。为了进一步提高计算效率，可以将ALSRTM与平面波震源编码、相位编码、GPU加速等方法结合，使其更好地适应实际地震资料处理。

感谢中国石油大学(华东)地震波传播与成像(SWPI)课题组的支持。感谢开源软件Madagascar (http://www.ahay.org/RSF) 提供的技术支持。

参考文献

[1] Youn O K,Zhou H W.Depth imaging with multiples.SEG Technical Program Expanded Abstracts,1999,18:246-255.

[2] Claerbout J F,Johnson A G.Extrapolation of time-dependent waveforms along their path of propagation.Geophysical Journal International,1971,26(3):285-293.

[3] 刘红伟,刘洪,邹振等.地震叠前逆时偏移中的去噪与存储.地球物理学报,2010,53(9):2171-2180.

Liu Hongwei,Liu Hong,Zou Zhen et al.The problems of denoise and storage in seismic reverse time migration.Chinese Journal of Geophysics,2010,53(9):2171-2180.

[4] Xu S,Chen F,Tang B et al.Noise removal by migration of time-shift images.Geophysics,2014,79(3):S105-S111.

[5] Robin F F,Paul F,Phil K et al.Suppressing artifacts in prestack reverse time migration.SEG Technical Program Expanded Abstracts,2005,24:2049-2051.

[6] 李闯,黄建平,李振春等.预条件最小二乘逆时偏移方法.石油地球物理勘探,2016,51(3):513-520.

Li Chuang,Huang Jianping,Li Zhenchun et al.Preconditioned least-squares reverse time migration.OGP,2016,51(3):513-520.

[7] Guitton A,Kaelin B,Biondi B.Least-square attenuation of reverse time migration artifacts.Geophysics,2007,72(1):S19-S23.

[8] Baysal E,Dan D K,Sherwood J W C.A two-way nonreflecting wave equation.Geophysics,2012,49(2):132-141.

[9] Yoon K,Marfurt K J.Reverse-time migration using the Poynting vector.Geophysical Exploration,2006,37(1):102-107.

[10] Liu F,Zhang G,Morton S A et al.An effective imaging condition for reverse-time migration using wavefield decomposition.Geophysics,2011,76(1):S29-S39.

[11] Rocha D C J.Wavefield imaging using the energy norm.Geophysics,2015,81(4):S151-S163.

[12] Op’t Root T J P M,Stolk C C and de Hoop M V.Linearized angular filtering based on seismic reverse time migration.Journal De Mathématiques Pures Et Appliqués,2012,98(2):211-238.

[13] Whitmore N D,Crawley S.Applications of RTM inverse scattering imaging conditions.SEG Technical Program Expanded Abstracts,2012,31:1-6.

[14] Kiyashchenko D,Plessix R E,Kashtan B et al.A modified imaging principle for true-amplitude wave-equation migration.Geophysical Journal International,2007,168(3):1093-1104.

[15] Tarantola A.Linearized inversion of seismic reflection data.Geophysical Prospecting,1984,32(6):998-1015.

[16] Nemeth T,Wu C,Schuster G T.Least-squares migration of incomplete reflection data.Geophysics,1999,64(1):208-221.

[17] Költzsch P.Inverse problems of acoustic and elastic waves.ZAMM,1986,66(9):447-447.

[18] Li C,Huang J P,Li Z C et al.Regularized least-squares migration of simultaneous-source seismic data with adaptive singular spectrum analysis.Petroleum Science,2017,14(1):61-74.

[19] Plessix R E,Mulder W A.Frequency-domain finite-difference amplitude-preserving migration.Geophysical Journal International,2004,157(3):975-987.

[20] Dai W,Schuster J.Least-squares migration of simul-taneous sources data with a deblurring filter.SEG Technical Program Expanded Abstracts,2009,28:4338.

[21] Dai W,Schuster G T.Plane-wave least-squares reverse-time migration.Geophysics,2013,78(4):S165-S177.

[22] 黄建平,曹晓莉,李振春等.最小二乘逆时偏移在近地表高精度成像中的应用.石油地球物理勘探,2014,49(1):107-112.

Huang Jianping,Cao Xiaoli,Li Zhenchun et al.Least square reverse time migration in high resolution imaging of near surface.OGP,2014,49(1):107-112.

[23] 李振春,李闯,黄建平等.基于先验模型约束的最小二乘逆时偏移方法.石油地球物理勘探,2016,51(4):738-744.

Li Zhenchun,Li Chuang,Huang Jianping et al.Regularized least-squares reverse time migration with prior model.OGP,2016,51(4):738-744.

[24] 李闯,黄建平,李振春等.平面波最小二乘逆时偏移编码策略分析.石油物探,2015,54(5):592-601.

Li Chuang,Huang Jianping,Li Zhenchun et al.Analysis on the encoding strategies of plane-wave least-square reverse time migration.GPP,2015,54(5):592-601.

[25] 黄建平,孙郧松,李振春等.一种基于分频编码的最小二乘裂步偏移方法.石油地球物理勘探,2014,49(4):702-707.

Huang Jianping,Sun Yunsong,Li Zhenchun et al.Least-squares split-step migration based on frequency-division encoding.OGP,2014,49(4): 702-707.

[26] Stolk C C,Symes W W.Kinematic artifacts in pre-stack depth migration.Geophysics,2004,69(2):562-575.

[27] Evans L.Partial Differential Equations(Second Edition).Wadsworth & Brooks/cole Mathematics,Berkeley,California,American,2010.

[28] 黄建平,刘培君,李庆洋等.一种棱柱波逆时偏移方法及优化.石油物探,2016,55(5):719-727.

Huang Jianping,Liu Peijun,Li Qingyang et al.An optimized reverse time migration approach for the prism wave.GPP,2016,55(5):719-727.