基于Chebyshev多项式的三维射线追踪

苗 贺 孙建国 王 蕤 颜鸿群 尹 畅 魏脯力(吉林大学地球探测科学与技术学院，吉林长春 130026)

1 引言

射线追踪在地震勘探的各个领域得到了广泛的应用，同时对于油气勘探中出现的复杂横向非均匀介质的正反演问题，提供了有力的解决手段。目前求解射线路径的方法有很多，但大体分为两类：一类是基于射线追踪方程的拉格朗日法，它关注的是一点在地震波场中的运动轨迹，在计算过程中能够同时计算出射线路径和旅行时，但是这种方法计算速度慢，且存在盲区；另一类是对程函方程进行数值分析的欧拉法，它关注的是固定网格点上行进的时间，因为在这种方法中唯一的控制方程是程函方程，相较于拉格朗日法，其计算速度要快得多，且不存在盲区，但是程函方程本身不能给出任何关于波传播的方向，计算的正确性需要使用费马原理进行检查[1]，有限差分法[2,3]、最短路径法[4-6]和旅行时线性插值法(LTI)[7-9]是三种具有代表性的方法[10]。有限差分法通过对程函方程在矩形网格上做差分离散近似计算给定速度模型的旅行时。最短路径法是在计算区域内形成一个由节点间的射线路径构成的网络图，然后根据Fermat原理选取旅行时最小的路径作为射线路径。Asakawa等[11]将LTI作为一种独立的旅行时计算方法提出，并给出了相应的射线路径计算方法。该方法是基于网格单元模型计算边界插值点的旅行时，并运用Fermat原理选取具有最小旅行时的射线路径。三维情况下LTI极小值问题为超越方程，一些学者采用网格界面剖分法[12]、快速插值法[13]、最速下降法[14]求解。然而，无论哪一种方法，其射线追踪的步长都会受到网格限制，即次级震源点只能位于网格界面或节点上[10]，这会给路径的求取带来误差。

旅行时场梯度法求取射线路径可以很好地解决这一问题。旅行时场梯度法利用已知的旅行时场求得各级震源处的旅行时及其梯度。Rawlinson等[15,16]首先通过快速匹配追踪法(Fast Marching Method，FMM)求取旅行时，然后在接收点沿旅行时梯度追踪到震源点，旅行时梯度的求取通过一种类似于迎风方法的有限差分近似得到； 张东等[10]应用B样条插值方法获得连续的旅行时场，故追踪步长不受网格尺寸的限制从而克服计算区域离散化所带来的问题，但在速度突变区域计算次级源点的旅行时和梯度会产生一定的误差[17]。通过采用函数逼近的方法能够从根本上解决这个问题，本文应用Chebyshev多项式逼近旅行时场、计算旅行时场梯度，不仅提高了射线路径的精度，而且提高了计算效率。

2 三维旅行时场计算方法

FMM无条件稳定且计算速度快，是一种满足波前传播规律的波前扩展方式(窄带技术)[18-22]。3D情况下的程函方程为

=s2(x,y,z)

(1)

(2)

(3)

式中h为网格间距。因为计算点的其中一个邻居点一定是窄带技术选取的局部最小旅行时点，而该点的旅行时必为已知。将三个方向上选取的差分格式代入式(2)中即可计算点(i,j,k)的旅行时梯度。FMM在实现时引入窄带技术用于波前的近似模拟，运用堆选排技术选取波前上(窄带内)的最小旅行时点作为扩展点，通过设定网格节点的属性“冻结”被认为已经完成计算的网格节点，并利用窄带内网格节点的更新近似地模拟波前的扩展演化[23-27]。

3 射线路径计算方法

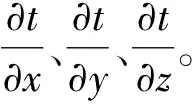
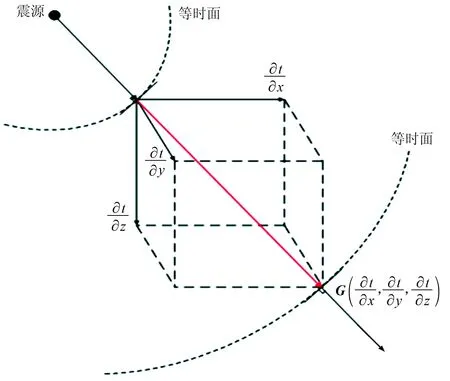
图1 射线传播路径示意图

3.1 一维逼近函数

函数逼近的定义为：设f(x)为[a，b]上的连续函数，由于其表达式难于求解，只能给出其在有限个点上的值，需要寻求一个近似函数P(x)(多项式)，使P(x)与f(x)在[a，b]上的误差在某种意义下最小。逼近函数的基函数有很多种，例如：正交多项式、三次样条插值、Pade逼近等。由于Chebyshev正交多项式能使插值余项达到最小，从而获得最准确的射线路径，所以选择Chebyshev正交多项式为基函数建立逼近函数。

第一类Chebyshev多项式Tn(x)的前四项为

(4)

取其前三项作为基函数，可得二阶逼近函数为

P(x) =a0T0(x)+a1T1(x)+a2T2(x)

=a0+a1x+a2(2x2-1)

(5)

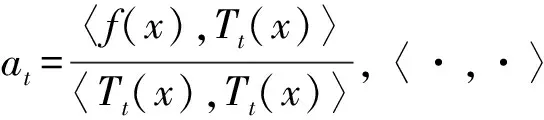
3.2 三维逼近函数

根据一维的二阶逼近函数，可得三维二阶逼近函数为

(6)

F(x,y,z)=a0+a1z+a2(2z2-1)+a3y+a4yz+a5y(2z2-1)+a6(2y2-1)+a7z(2y2-1)+a8(2y2-1)(2z2-1)+a9x+a10xz+

a11x(2z2-1)+a12xy+a13xyz+a14xy(2z2-1)+a15x(2y2-1)+a16(2y2-1)xz+

a17x(2y2-1)(2z2-1)+a18(2x2-1)+

a19(2x2-1)z+a20(2x2-1)(2z2-1)+

a21(2x2-1)(2y2-1)+a22(2x2-1)y+

a23(2x2-1)yz+a24(2x2-1)y(2z2-1)+

a25(2x2-1)(2y2-1)z+a26(2x2-1)×

(2y2-1)(2z2-1)

(7)

可写为

(8)

式中Tt为正交函数簇，其系数为

(9)

(10)

为保证各项基函数正交，网格节点需要进行如图2所示局部坐标变换

(11)

经坐标变换后，应用式(9)求取多项式系数，再代入式(7)中可得到三维逼近函数。

与B样条插值采用4×4×4网格不同，Chebyshev插值坐标变换网格是以当前追踪点最临近网格点为中心点的局部3×3×3网格。

对三维的逼近函数F(x，y，z)求导，即可求得旅行时场梯度

a13yz+a14y(2z2-1)+a15(2y2-1)+

a16(2y2-1)z+a17(2y2-1)(2z2-1)+

4a18x+4a19xz+4a20x(2z2-1)+

4a21x(2y2-1)+4a22xy+4a23xyz+

4a24xy(2z2-1)+4a25x(2y2-1)z+

4a26x(2y2-1)(2z2-1)

(12)

图2 插值网格示意图(a)插值网格； (b)插值坐标变换网格

4a7yz+4a8y(2z2-1)+a12x+a13xz+

a14x(2z2-1)z+4a15xy+4a16xyz+

4a17xy(2z2-1)+4a21y(2x2-1)+

a22(2x2-1)+4a23xy+a24(2x2-1)(2z2-1)+4a25yz(2x2-1)+4a26y(2x2-1)(2z2-1)

(13)

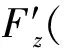
4a14xyz+a16(2y2-1)x+4a17xz(2y2-1)+a19(2x2-1)+4a20z(2x2-1)+a23(2x2-1)y+4a24yz(2x2-1)+a25(2x2-1)(2y2-1)+4a26z(2x2-1)(2y2-1)

(14)

4 数值模拟

应用速度连续变化模型和Marmousi模型，对Chebyshev插值射线追踪算法与B样条插值射线追踪算法进行对比分析。

4.1 速度连续变化模型

模型尺寸为500m×500m×500m，网格间距为10m，源点置于(1.0m，1.0m，1.0m)点处，接收点位于模型上表面均匀分布，间距为20m。模型的速度分布函数为(500+60z)(单位为m/s)。图3a为Chebyshev插值法计算的射线路径，图3b为B样条插值方法计算的射线路径。图4a和图4b对比了两种方法在y=25m处的xz剖面射线路径，二者整体相差不大，只是Chebyshev方法计算的射线路径在源点附近精度要高一些。图5为两种方法的旅行时相对误差对比，可以看出，Chebyshev插值法精度明显高于B样条插值法。采用同样的计算机硬件(酷睿i5 2450M/CPU，6G/RAM)，Chebyshev插值法用时为4.205s，B样条插值法用时为5.191s，效率提高了约20%。

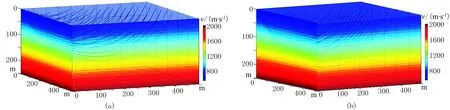
图3 速度连续变化模型两种方法射线路径三维对比(a)Chebyshev插值法； (b)B样条插值法

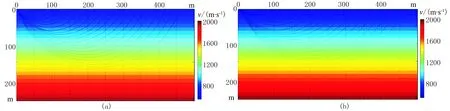
图4 速度连续变化模型两种方法射线路径剖面对比(a)B样条插值法； (b)Chebyshev插值法

图5 速度连续变化模型两种方法计算的旅行时误差

4.2 Marmousi模型

为了检验本文算法在面对复杂介质时的有效性，由二维Marmousi模型生成的三维模型，模型尺寸为3800m×3800m×1220m，计算时采用的网格间距为10m，震源置于(0，0，0)处。接收点位于模型上表面、下底面与右侧面均匀分布，间距为100m。图6a为FMM计算的二维模型旅行时分布。图6b和图6c分别为B样条插值和Chebyshev插值法计算的二维射线路径，每条射线都垂直于等时线。 由图5d和图5e可见，两种方法都能够很好地求解复杂模型的三维射线路径。但对比两种方法的旅行时与原始旅行时场的相对误差可知，Chebyshev方法计算的路径误差比较小(图7)。另外，Chebyshev插值法用时为80.892s，B样条插值法用时为102.060s，前者效率较后者提高了约20%。

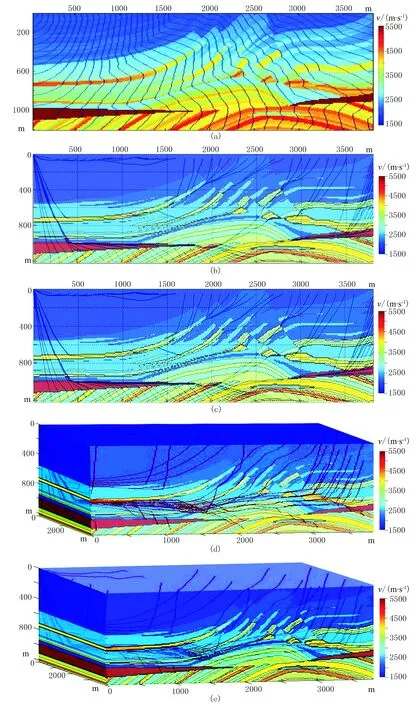
图6 Marmousi模型射线追踪结果(a)二维模型旅行时； (b)B样条插值法计算的二维射线路径； (c)Chebyshev插值法计算的二维射线路径； (d)Chebyshev插值计算的三维射线路径； (e)B样条插值计算的三维射线路径

5 结束语

本文应用Chebyshev插值法拟合旅行时场并求取旅行时场梯度，避免了对离散旅行时场的数值求导过程。相较于B样条插值法，Chebyshev插值法能够较好地得到计算区域内任一点的梯度，从而获得更准确的射线路径。数值实验表明该方法在构造复杂时精度优于B样条插值法射线追踪，且运行效率高于B样条插值法。本文射线追踪方式为单条追踪，如果能够同时计算出多个接收点的路径，势必能够大幅提升计算效率。

参考文献

[1] Sun J，Sun Z，Han F.A finite difference scheme for solving the eikonal equation including surface topo-graphy.Geophysics，2011，76(4)：T53-T63.

[2] Vidale J E.Finite-difference calculation of traveltimes in 3-D.SEG Technical Program Expanded Abstracts，1989，8：1096-1098.

[3] Vidale J.Finite-difference calculation of travel times.Bulletin of the Seismological Society of America，1988，78(6)：2062-2076.

[4] Moser T J.Shortest path calculation of seismic rays.Geophysics，1991，56(1)：59-67.

[5] 唐小平，白超英，刘宽厚.分区多步最短路径极值法多值多次反射波追踪.地球物理学进展，2011，26(6)：2064-2074.

Tang Xiaoping，Bai Chaoying，Liu Kuanhou.Multiva-lued and multiple reflected raytracing with extreme value based on the multistage modified shortest-path method.Progress in Geophysics，2011，26(6)：2064-2074.

[6] 赵后越，张美根.起伏地表条件下各向异性地震波最短路径射线追踪.地球物理学报，2014，57(9)：2910-2917.

Zhao Houyue，Zhang Meigen.Tracing seismic shortest path rays in anisotropic medium with roiling surface. Chinese Journal of Geophysics，2014，57(9)：2910-2917.

[7] 李培明，梅胜全，马青坡.一种改进的双线性插值射线追踪方法.石油地球物理勘探，2013，48(4)：553-558.

Li Peiming，Mei Shengquan and Ma Qingbo.An improved bilinear interpolation travel-time ray-tracing method.OGP，2013，48(4)：553-558.

[8] 韩复兴，孙建国，杨昊.基于二维三次卷积插值算法的波前构建射线追踪.吉林大学学报(地球科学版)，2008， 38(2)：336-340.

Han Fuxing，Sun Jianguo，Yang Hao.Ray-tracing of wavefront construction by bicubic convolution interpolation.Journal of Jilin University (Earth Science Edition)，2008，38(2)：336-340.

[9] 张婷婷，张东，邱达.三维层状介质中基于旅行时梯度的多次波射线追踪.石油地球物理勘探，2014，49(6)：1097-1105.

Zhang Tingting，Zhang Dong and Qiu Da.Multiple ray tracing in 3D layered media using the traveltime gradient method.OGP，2014，49(6)：1097-1105.

[10] 张东，张婷婷，乔友锋等.三维旅行时场B样条插值射线追踪方法.石油地球物理勘探，2013，48(4)：559-566.

Zhang Dong，Zhang Tingting，Qiao Youfeng et al.A 3-D ray tracing method based on B-spline traveltime interpolation.OGP，2013，48(4)：559-566.

[11] Asakawa E，Kanawa T.Seismic ray tracing using linear traveltime interpolation.Geophysical Prospecting，1993，41(1)：99-111.

[12] 张东，傅相如，杨艳等.基于LTI和网格界面剖分的三维地震射线追踪算法.地球物理学报，2009，52(9)：2370-2376.

Zhang Dong，Fu Xiangru，Yang Yan et al.3-D seismic ray tracing algorithm based on LTI and partition of grid interface.Chinese Journa of Geophysics，2009，52(9)：2370-2376.

[13] 刘锋，张东，杨艳等.三维LTI射线追踪极小值方程的快速数值解法.武汉大学学报(理学版)，2012，58(5)：395-400.

Liu Feng，Zhang Dong，Yang Yan et al.A fast nume-rical solution to minimum equation in 3-D seismic LTI ray tracing.Journal of Wuhan University (Natural Science Edition).2012，58(5)：395-400.

[14] 金昌昆，张建中.共接收面元三维折射旅行时反演方法.石油地球物理勘探，2016，51(4)：751-759.

Jin Changkun and Zhang Jianzhong.3D refraction traveltime inversion in common receiver-bins. OGP，2016，51(4)：751-759.

[15] Rawlinson N，Sambridge M.Wave front evolution in strongly heterogeneous layered media using the fast marching method.Geophysical Journal International，2004，156(3)：631-647.

[16] Rawlinson N，Sambridge M.Multiple reflection and transmission phases in complex layered media using a multistage fast marching method.Geophysics，2004，69(5)：1338-1350.

[17] 张婷婷，邱达，张东.一种改进的三维旅行时梯度射线追踪方法.石油地球物理勘探，2016，51(5)：916-923.

Zhang Tingting，Qiu Da and Zhang Dong.A modified 3D traveltime gradient ray tracing method.OGP，2016，51(5)：916-923.

[18] Sethian J A.Evolution，implementation and applica-tion of level set and fast marching methods for advancing fronts.Journal of Computational Physics，2001，169(2)：503-555.

[19] Sethian J A.A fast marching level set method for monotonically advancing fronts.Proceedings of the National Academy of Sciences，1996，93(4)：1591-1595.

[20] 黄兴国，孙建国，孙章庆等.基于复程函方程和改进的快速推进法的复旅行时计算方法.石油地球物理勘探，2016，51(6)：1109-1118.

Huang Xingguo，Sun Jianguo，Sun Zhangqing et al.A perturbation approach for solving the TTI complex eikonal equation.OGP，2016，51(6)：1109-1118.

[21] 李永博，李庆春，吴琼等.快速行进法射线追踪提高旅行时计算精度和效率的改进措施.石油地球物理勘探，2016，51(3)：467-473.

Li Yongbo，Li Qingchun，Wu Qiong et al.Improved fast marching method for higher calculation accuracy and efficiency of traveltime.OGP，2016，51(3)：467-473.

[22] 王飞，曲昕馨，刘四新等.一种新的基于多模板快速推进算法和最速下降法的射线追踪方法.石油地球物理勘探，2014，49(6)：1106-1114.

Wang Fei，Qu Xinxin，Liu Sixin et al.A new ray tra-cing approach based on both multi-stencils fast mar-ching and the steepest descent.OGP，2014，49(6)：1106-1114.

[23] 张风雪，吴庆举，李永华等.FMM射线追踪方法在地震学正演和反演中的应用.地球物理学进展，2010，25(4)：1197-1205.

Zhang Fengxue，Wu Qingju，Li Yonghua et al.Application of FMM ray tracing to forward and inverse problems of seismology.Progress in Geophysics，2010，25(4)：1197-1205.

[24] 邓飞，刘超颖.三维射线快速追踪及高斯射线束正演.石油地球物理勘探，2009，44(2)：158-165.

Deng Fei，Liu Chaoying.3-D rapid ray tracing and Gaussian ray beam forward simulation.OGP，2009，44(2)：158-165.

[25] 李晓玲，白超英，胡光义.起伏层状TI介质中多次波射线追踪.石油地球物理勘探，2013，48(6)：924-931.

Li Xiaoling，Bai Chaoying and Hu Guangyi.Multiple ray tracing in an undulated layered TI media.OGP，2013，48(6)：924-931.

[26] 唐秋惠，薛霆虓，何诚.三维多步FMM射线追踪在正态分布速度地层模型中的应用.工程地球物理学报，2017，14(3)：346-352.

Tang Qiuhui，Xue Tingxiao，He Cheng.The application of multi-stage 3D fast marching method of ray tracing in normal distribution speed model.Chinese Journal of Engineering Geophysics，2017，14(3)：346-352.

[27] 孙章庆，孙建国，岳玉波等.复杂山地随机介质GMM-ULTI法射线追踪.地球物理学报，2016，59(7)：2615-2627.

Sun Zhangqing，Sun Jianguo，Yue Yubo et al.Ray tracing using GMM-ULTI method in the random media with complex topography.Chinese Journal of Geophysics，2016，59(7)：2615-2627.