基于高斯束偏移的鬼波压制

吴 娟 白 敏 张 华(华北水利水电大学资源与环境学院，河南郑州 450046； ②东华理工大学地球物理与测控技术学院，江西南昌 330013)

1 引言

海洋地震勘探中，鬼波一直是影响资料品质的一个重要因素。由自由表面产生的炮点和接收点鬼波导致地震记录频率与角度相关的效应，引起振幅畸变，往往严重干扰一次波，降低分辨率，甚至会产生虚假同相轴。因此，要获得一个更加连续的、包含岩性信息的成像剖面，必须在采集或数据处理时设法消除鬼波的影响，增强地震资料的可解释性，提高勘探精度[1]。

采集方面，宽频地震采集技术是近年来一个比较活跃的课题，主要包括上下源、上下缆、双检以及倾斜缆等采集方式。基于上下缆合并处理技术，Sønneland等[2]提出了基于波场延拓算法压制垂直接收缆中鬼波的方法； Posthumus[3]提出了相位加权求和法提取上行波的计算方法； Hill等[4]指出上下缆采集技术将是地震勘探下一阶段的飞跃；Grata-cos[5]通过几种最小二乘数据融合方法得到上下缆资料中地表的上行波场，利用三维算法在f-x-y域实现鬼波补偿； Özdemir等[6]利用最小二乘上下缆最优组合算法，提出了最优鬼波压制方法； 刘春成等[7]指出上下缆合并效果与上下缆沉放深度密切相关，提出利用上下缆合并算子确定上下缆采集的最优沉放深度组合； He等[8]研究了一种自适应的上下缆地震数据合并技术，在保留传统方法得到的鬼波算子相位谱的同时，利用数据本身进一步自适应地估计鬼波算子的振幅谱，进而实现上下缆数据的合并补偿鬼波； 赵仁永等[9]采用上下源、上下缆方式在珠江口盆地进行地震数据采集试验，改进了复杂地区的地震成像效果。

对于常规采集的地震资料，同样可以在处理中压制鬼波，提高分辨率。Soubaras[10]同时对数据做偏移和镜像偏移，将得到的两个剖面做联合反褶积，提出适应任何采集方式的鬼波补偿算法。Wang等[11]利用自适应迭代在局部时窗内确定鬼波的延迟时间，通过原始数据和由原始数据生成的镜像数据，在偏移之前去除炮点和接收点鬼波。但镜像数据生成不准确会导致上、下行波之间实际延迟时间计算的误差。顾汉明等[12]采用最小二乘反演迭代最优化算法计算平均延迟时间和上行波记录，鬼波压制取得较好的效果，并应用于荔湾深水变深度缆宽频处理。许自强等[13]将最优化联合反褶积算法应用到变深度缆采集数据的处理中。

炮点和检波器鬼波补偿既可以在偏移之前[11]进行，也可以在偏移过程中[14]完成。利用偏移成像消除与自由表面相关的鬼波效应，增强地质可解释性，也是当前海洋地震勘探面临的挑战之一。Sablon等[15]、Soubaras[16]运用镜像偏移处理技术有效压制虚反射。许多学者通过鬼波补偿提高成像分辨率，以得到更加连续、含有岩性信息的剖面，增强地质可解释性，为地震反演提供一个更稳健的初始模型。Zhang等[14]基于真振幅偏移理论，提出了在逆时偏移中补偿炮点和接收点鬼波的方法。数值试验表明，通过压制鬼波能提高地震记录的分辨率和保真度，在成像时可更好地刻画低频地质变化。Roberts等[17]提出在共炮检距道集束偏移中压制鬼波的方法，利用束偏移在倾斜叠加域实现的特点，把炮点和接收点鬼波补偿算子加入偏移算法中。

本文采用Roberts等的思路，利用共炮集高斯束偏移[18-23]压制鬼波的方法，并给出稳定求解鬼波补偿算子，达到消除鬼波影响的目的。数值试验结果表明，鬼波压制能使偏移剖面的同相轴连续性增强、分辨率提高。

2 方法原理

利用高斯束积分表征的格林函数[24]为

(1)

式中：uGB表示高斯束波场；x=(x，z)为地下任一点；xS=(xS,zS)为震源点坐标；ω为角频率；p=(px，pz)为中心射线的参数矢量， 其中px和pz分别为射线参数的水平分量和垂直分量。共炮点道集高斯束叠前成像公式[25]为

(2)

式中：u(xR,xS,ω)为记录波场；xR=(xR,zR)表示接收点坐标；ICS(x)为最终的叠前成像值；上标“*”表示复共轭。G*对zR的偏导数为

(3)

高斯函数具有如下性质

(4)

式中：LR为接收点的束中心；pLRz为束中心LR处射线参数的垂直分量；ωr为参考频率； ΔL为束中心间隔；L0表示ωr下的初始束宽。将式(4)代入式(2)，可得

(5)

式中G(x,xS,ω)为源点格林函数，其表达式为

(6)

其中pSx和pSz分别表示源点的射线参数水平分量和垂直分量。束中心LR有效范围内接收点的格林函数G(x,xR,ω)可表示为

exp[-iωpLR·(xR-LR)]

(7)

将源点和接收点格林函数分别代入式(5)，可得

exp[iωpLR·(xR-LR)]

(8)

式(8)可简化为

(9)

式(9)即为最终的叠前共炮点道集高斯束偏移公式。式中：pLR=(pLRx,pLRz)是接收点射线参数，DS(LR,pLR,ω)为地震记录的加窗局部倾斜叠加，可表示为

(10)

式(10)中假设地震记录同时包含了震源和接收点鬼波。

为了消除鬼波的影响，采用Roberts等[17]的思路，并将DS(LR,pLR,ω)替换为

(11)

(12)

式中：v为海水速度；A是震源和接收点鬼波补偿算子在倾斜叠加域的表达式。

直接利用式(11)进行补偿会导致数值计算不稳定，需要在波场传播过程中加入一些稳定算法。本文通过在分母上加上一个很小的数解决数值计算的稳定性问题，即

(13)

式中ε的取值范围为0.01～0.1。

3 数值试验

应用两个模型实例检验共炮道集高斯束偏移压制鬼波的效果。

3.1 层状模型

层状模型如图1所示，网格数为301×301，纵、横向网格间距Δx=Δz=5m。合成记录炮点位于横向距离750m处，共301个接收点，时间采样点数为1024，采样间隔为2ms，炮点和接收点深度均为10m。为了对比，同时模拟没有鬼波的地震数据(原始数据)。

图2a为原始单炮数据，图2b为模拟的含有炮点和接收点鬼波的地震数据，可以看出，原始数据由一个波峰和两个波谷组成，分辨率较高，而含有鬼波的数据，由于鬼波的调谐作用，变成两个波峰一个波谷，相位发生畸变。图2c为逆散射级数(ISS)法压制鬼波后的地震数据，由图可知，ISS法很好地消除了鬼波的影响，同相轴重新变为一个波峰，且相位得到校正。

图1 层状模型

图2 简单模型数据鬼波压制结果(a)原始数据； (b)含有鬼波的数据； (c)ISS法压制鬼波后的数据

从图2a～图2c中抽出部分道(间隔10道抽取一道)进行局部波形显示，结果如图3a～图3c所示，图3d为ISS法压制鬼波后的数据与原始数据的残差。从波形图可以看出， ISS方法压制鬼波后，消除了由鬼波造成的旁瓣，同时保持了子波的原始相位。在图3d的残差数据中，第1500m处误差较大，是ISS算法里面傅里叶变换的周期效应所致，可以通过扩充模型或者在模型两侧加吸收衰减层消除。

该例说明了ISS方法压制鬼波的效果较好。以ISS方法去除鬼波的偏移结果为参照，检验共炮道集高斯束偏移压制鬼波的有效性。

图4a和图4b分别为对原始数据、含有鬼波数据的常规高斯束偏移结果，图4c为ISS法压制鬼波后数据的偏移结果，图4d为采用本文方法压制鬼波后的偏移结果。

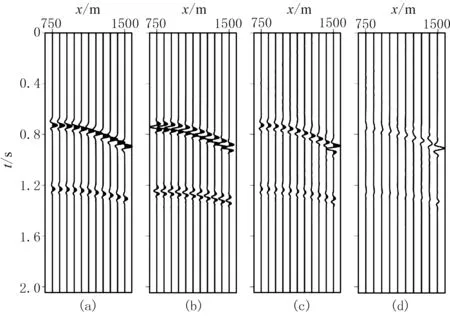
图3 图2数据抽稀波形显示(a～c)及ISS法鬼波

对比图4b与图4c可以看出，本文方法也很好地消除了鬼波的影响。偏移剖面中，同相轴的相位得以校正，得到了一次波的像， 与ISS法压制鬼波后的数据偏移结果一致，提高了分辨率。

3.2 SMAART数据

利用经典的SMAART数据对算法进行测试。模型(图5)尺寸为22860m×9151.62m，网格数为3000×1201，网格间距Δx=Δz=7.62m，炮检距和道间距均为22.76m，时间样点数为1126，采样间隔为8ms，炮点及接收点的深度均为7.62m。

为了更好地对比去除鬼波前后的效果，偏移前先利用SRME方法去除了炮集中的其他多次波。

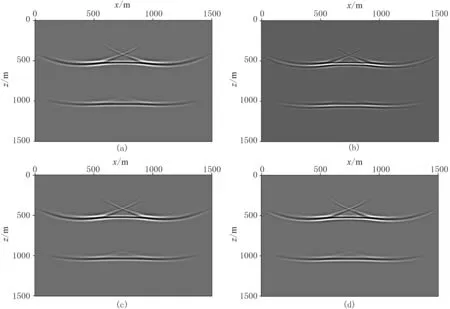
图4 不同数据偏移结果对比(a)原始； (b)含鬼波； (c)ISS法鬼波压制后； (d)本文方法鬼波压制后

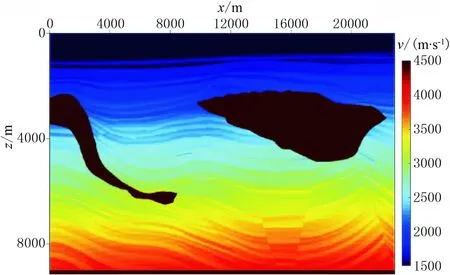
图5 SMAART速度模型

在进行共炮集高斯束偏移压制鬼波测试时，共选用1000炮，每炮540道。

图6a为未压制鬼波数据的常规高斯束偏移结果，图6b为本文方法压制鬼波后的高斯束偏移结果。由图可以看出，压制鬼波以后，一次波的能量增强，相位得到校正，深层同相轴更清晰、连续，盐丘体的边界刻画更准确。整个偏移剖面的成像效果较好，分辨率得到提高。

为了更清晰地对比压制鬼波前后的效果，选取图6局部(实线和虚线框所示)进行放大波形显示(图7和图8)。

实线框内区域位于盐丘的顶部，虚线框内区域位于模型的深部，由图中红色框和箭头标识处可知：鬼波衰减后，子波由原先的多个波峰和波谷还原为形状较好的单波峰子波，初至相位能量比较强，尾随一次波之后的鬼波得到了较彻底的压制。与鬼波衰减前的剖面相比，衰减鬼波后的同相轴更为清晰，有效反射波更为突出，成像剖面的地质构造可解释性增强。

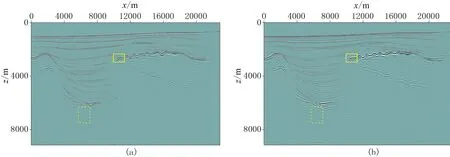
图6 SMAART速度模型数据偏移对比(a)未压制鬼波偏移剖面； (b)压制鬼波后偏移剖面

图7 图6实线框内局部数据波形放大显示(a)压制鬼波前；(b)压制鬼波后

图8 图6虚线框内局部数据波形放大显示(a)压制鬼波前； (b)压制鬼波后

4 结论

本文研究了共炮集高斯束偏移在压制鬼波中的应用。在偏移过程中补偿炮点和接收点鬼波，以达到提高成像分辨率、增强地质可解释性的目的，并给出稳定补偿的算法。数值试验证明，鬼波压制后偏移结果的深层能量增强，分辨率提高，反射同相轴更连续，断点更清晰，有利于后续的解释和反演。

参考文献

[1] 陈金海，王桂华，徐新南.海上地震虚反射探讨.海洋石油，2000，20(1)：23-27.

Chen Jinhai，Wang Guihua，Xu Xinnan.Assessment of ghosts in marine seismic data.Offshore Oil，2000，20(1)：23-27.

[2] Sønneland L，Berg L E，Eidsvig P et al.2-D deghos-ting using vertical receiver arrays.SEG Technical Program Expanded Abstracts，1986，5：516-519.

[3] Posthumus B J.Deghosting of twin streamer configuration.Geophysical Prospecting，1993，41(3)：267-286.

[4] Hill D，Combed L，Bacon J.Over/under acquisition and data processing：the next quantum leap in seismic data technology? First Break，2006，24(6)：81-95.

[5] Gratacos B.Over-under deghosting：1D，2D or 3D algorithms in the F，FK or FXY domains.70th EAGE Conference and Exhibition Extended Abstracts，2008，H011.

[6] Özdemir A K，Caprioli P，Özbek A et al.Optimized deghosting of over/under towed-streamer data in the presence of noise.The Leading Edge，2008，27(2)：190-199.

[7] 刘春成，刘志斌，顾汉明.利用上/下缆合并算子确定海上上/下缆采集的最优沉放深度组合.石油物探，2013，52(6)：623-629.

Liu Chuncheng，Liu Zhibin，Gu Hanming.The determination of optimal sinking depths of over/under streamers in offshore survey by merge operator.GPP，2013，52(6)：623-629.

[8] He J W，Lu W K，Li Z X et al.An adaptive over/under data combination method.Applied Geophysics，2013，10(4)：469-476.

[9] 赵仁永，张振波，轩义华.上下源、上下缆地震采集技术在珠江口的应用.石油地球物理勘探，2011，46(4)：517-521.

Zhao Renyong，Zhang Zhenbo，Xuan Yihua.Application of over/under streamer and over/under source seismic acquisition in the Pearl River Mouth Basin.OGP，2011，46(4)：517-521.

[10] Soubaras R.Deghosting by joint deconvolution of a migration and a mirror migration.SEG Technical Program Expanded Abstracts，2010，29：3406-3410.

[11] Wang P，Peng C.Premigration deghosting for marine towed streamer data using a bootstrap approach.SEG Technical Program Expanded Abstracts，2012，31：1-5.

[12] 顾汉明，王冲，许自强等.反演迭代算法在海上斜缆采集资料宽频处理中的应用.第十七届中国科协年会“南海深水油气勘探开发技术”研讨会论文集， 2015.

[13] 许自强，方中于，顾汉明等.海上变深度缆数据最优化压制鬼波方法及其应用.石油物探，2015，54(4)：404-413.

Xu Ziqiang，Fang Zhongyu，Gu Hanming et al.The application of optimal deghosting algorithm on marine variable-depth streamer data.GPP,2015,54(4):404-413.

[14] Zhang Y，Roberts G，Khalil A.Compensating for source and receiver ghost effects in reverse time migration.SEG Technical Program Expanded Abstracts，2012，31：4609-4613.

[15] Sablon R，Russier D，Zurita O et al.Multiple attenuation for variable-depth streamer data：from deep to shallow water.SEG Technical Program Expanded Abstracts，2011，30：3505-3509.

[16] Soubaras R.Pre-stack deghosting for variable-depth streamer data.SEG Technical Program Expanded Abstracts，2012，31：780-789.

[17] Roberts G，Zhang Y，Poole G.Source and receiver ghost compensation within a beam migration.SEG Technical Program Expanded Abstracts，2013，32：3667-3671.

[18] Wu J，Chen X H，Bai M et al.Attenuation compensation in multicomponent Gaussian beam prestack depth migration.Applied Geophysics，2015，12(2)：157-168.

[19] Bai M，Chen X H，Wu J et al.Q-compensated migration by Gaussian beam summation method.Journal of Geophysics and Engineering，2016，13(1)：35-48.

[20] 白敏，陈小宏，吴娟等.基于吸收衰减补偿的多分量高斯束叠前逆时偏移.地球物理学报，2016，59(9)：3379-3393.

Bai Min，Chen Xiaohong，Wu Juan et al.Multiple-component Gaussian beam reverse-time migration based on attenuation compensation.Chinese Journal of Geophysics，2016，59(9)：3379-3393.

[21] 白敏.高斯束偏移方法与应用[学位论文].北京：中国石油大学(北京)，2016.

Bai Min.Theory and Application of Gaussian Beam Migration[D].China University of Petroleum(Beijing)，Beijing，2016.

[22] 刘强，张敏，李振春等.各向异性介质共炮域高斯束偏移.石油地球物理勘探，2016，51(5)：930-937.

Liu Qiang，Zhang Min，Li Zhenchun et al.Common-shot domain Gaussian beam migration in anisotropic media.OGP，2016，51(5)：930-937.

[23] 代福材，黄建平，李振春等.角度域黏声介质高斯束叠前深度偏移方法.石油地球物理勘探，2017，52(2)：283-293.

Dai Fucai，Huang Jianping，Li Zhenchun et al.Angle domain prestack Gaussian beam migration for visco-acoustic media.OGP，2017，52(2)：283-293.

[24] 白敏，吴娟，孙章庆等.基于全局笛卡尔坐标系的高斯束地震波场模拟.石油地球物理勘探，2018，53(2)：257-265.

Bai Min，Wu Juan,Sun Zhangqing et al.Seismic modeling by Gaussian beams in the global Cartesian coordinate system.OGP，2018，53(2)：257-265.

[25] 吴娟.基于衰减补偿的高斯束偏移方法研究[学位论文].北京：中国石油大学(北京)，2015.

Wu Juan.Research on Gaussian Beam Migration Me-thod Based on Attenuation Compensation[D].China University of Petroleum(Beijing)，Beijing，2015.