基于反射波动方程的地震反射数据波形成像

陈 生 昌(浙江大学地球科学学院，浙江杭州 310027)

1 概论

利用地震波可获取地下地质体的信息。地质体是由块状体和层状体组成，在地震勘探中这些块状体和层状体产生散射数据和反射数据。利用地震数据对这些地质体的反演成像有三个不同层次： ①反演地质体的物性参数，即所谓的地震数据全波形反演[1，2]，如果仅考虑一次波数据且初始模型较合适，则该全波形反演就退化为波形线性反演[3]； ②反演地质体的边界物性参数(如反射率或反射系数)； ③反演地质体的边界位置信息，即所谓的地震数据偏移(构造)成像。从由①反演出的地质体物性参数可得到地质体的边界物性参数和边界位置信息； 由②反演出的地质体边界物性参数可得到地质体的边界位置信息，但不能得到地质体的物性参数分布； 由③反演出的地质体边界位置信息不能得到地质体的物性参数和边界物性参数。

地震数据偏移成像是油气勘探开发中获取地下地质体三维构造(边界)图像的主要方法技术[4-7]，为构造型油气藏的勘探开发作出了巨大的贡献。随着油气勘探开发目标的日趋复杂化和精细化，如致密砂岩油气藏、页岩油气藏和火成岩油气藏等的勘探开发，人们希望把地震数据的第三层次的构造成像提升到第一层次的全波形反演或第二层次的边界物性参数反演，所得到的成像结果不仅能满足复杂构造成像的要求，还要能反映地下岩性的变化，以满足复杂油气藏勘探开发中地震数据岩性处理解释的需要。

现代地震数据偏移成像方法发源于上世纪70年代初期[8-11]，其目的是利用数学处理的方法把在地表观测到的地震反射波场送回到产生它的位置上去，以得到反映地下反射体位置信息的偏移成像波场[12-17]。经过四十余年的发展，偏移成像方法已从叠后走向了叠前，从二维走向了三维，从时间偏移成像走向了深度偏移成像，从各向同性介质走向了各向异性介质，从标量声波方程走向了矢量弹性波方程[18，19]，从不需迭代的常规偏移成像走向了真振幅偏移成像和基于迭代的最小二乘偏移成像[20-27]，并尝试通过角度域的真振幅偏移或最小二乘偏移实现速度和波阻抗反演[28，29]。

地震反射波的传播包含入射波传播、反射、反射波传播三个过程，在形式上可用Berkhout[30]提出的WRW概念模型表示。当前的偏移方法都是基于该反射波传播概念模型和Claerbout“时间一致性”成像原理或“爆炸反射面”原理发展起来的。因此偏移成像方法的实现显式或隐式地包含两步： 一是基于波动方程的波场外推； 二是基于“时间一致性”成像原理或“爆炸反射面”原理的成像。所谓的显式偏移成像方法是先进行波场外推然后再进行成像的偏移成像方法，如基于波动方程的单程波方程偏移成像方法[31-37]和双程波方程逆时偏移成像方法[38-41]；而所谓的隐式偏移成像方法是把波场外推和成像合二为一的偏移成像方法，如基于射线追踪的Kirchhoff积分偏移成像方法[42-44]和束偏移成像方法[45-47]。

在地震反射数据的逆时偏移中，假定偏移速度模型的运动学特征准确，基于波动方程的震源波场正向(顺时)外推是对炮点激发的入射波场的模拟，可以得到旅行时和振幅都正确的入射波场，而基于波动方程的记录波场逆时外推是对地震反射数据中反射传播的近似逆(伴随)传播，这种伴随传播可消除反射传播中的旅行时，但不能恢复反射传播中的振幅变化。因此，由记录波场逆时外推重建出的地下反射面上的反射波场相比于反射面上的真实反射波场，虽然有相同的旅行时，但振幅不同，而且分辨率低。Claerbout的“时间一致性”成像原理是对反射面处入射波场与反射波场间旅行时关系的定量描述，该成像原理在地震波传播的旅行时方面是满足波动方程的，但它不是由波动方程推导出来的。由基于“时间一致性”成像原理建立的成像公式，不论是反褶积形式的还是互相关形式的，所得到的偏移成像结果仅是指示地下反射面的存在位置，和反射面上的物性参数不存在数学物理意义上的联系，因为成像公式所表示的入射波场与反射波场间的关系是不满足波动方程的。基于Kirchhoff积分的叠前偏移成像方法(其对应的偏移成像计算式隐含了互相关成像公式)所得到的偏移成像结果也仅是指示反射面的存在位置和反射面上的物理参数也不存在数学物理意义上的联系，因为Kirchhoff积分仅是表示波场的传播，而没有考虑波场的反射。当前的地震反射数据偏移成像方法虽然波场外推或旅行时计算和振幅变化的计算是基于波动方程的，但由于其成像公式仅是由地震波的旅行时关系建立的，而不是由反射波传播所满足的波动方程推导出来的，所以本文认为当前的偏移成像方法不是一种完全的波动方程方法。

地震数据观测系统的不规则、不完整和反射面上覆介质物性变化会引起地震波的照明不均匀。逆时偏移中的地震波逆时外推既不能有效地消除地震波照明不均匀对反射波场重建的影响，也不能恢复地震波传播中的几何扩散效应，并由此造成偏移成像阴影和降低偏移成像分辨率。此外，互相关成像公式也会造成偏移成像阴影和偏移成像分辨率降低。为了消除逆时外推和互相关成像公式产生的偏移成像阴影和提高偏移成像结果的分辨率，人们提出了基于迭代求解方式的最小二乘偏移方法[48-52]。在当前的地震数据偏移中不区分散射和反射，当前的最小二乘偏移方法以一阶Born近似的散射波传播方程为基础，得到的是速度相对扰动变化，而不是对反射面位置的成像。此外，散射波方程仅适合地下介质速度的局部小扰动体产生的散射波，而对于地下介质中大尺寸(相对于地震波主波长)的速度异常体(层)所产生的地震反射波用散射波方程进行描述是不合适的。因此，本文认为当前反射数据最小二乘偏移成像方法所基于的正演方程不合适，求得的偏移成像结果也不是对反射面位置的成像。从地震数据偏移和反演的观点，当前的所谓最小二乘偏移仅是求取速度相对扰动的一种线性反散射方法，而不是一种以反射面位置为目标的偏移方法。本文认为基于当前的以获取反射面位置信息为目标的偏移成像方法是不能构建所谓的最小二乘偏移成像方法的，因为“时间一致性”原理成像公式所得到的反射面位置是一个几何变量，而不是一个物性参数变量，无法用于地震反射数据的反偏移，即目前还无法建立一个基于反射面位置信息的反射波传播方程，适合反射数据偏移成像的反射波动方程是建立反射数据最小二乘偏移的基础。

为了用波动理论描述地震数据偏移成像方法，Beylkin[53]和Bleistein[54]基于散射波动方程，利用地震反演中的线性反散射理论、拟微分算子理论和Fourier积分算子理论及其微局部分析，建立了一套严谨的完全基于散射波动方程的散射偏移成像方法，该方法对于局部弱散射体产生的散射地震数据具有很好的适应性，可实现对散射体位置的成像。对于反射体产生的地震反射数据的偏移成像，Bleistein等[15]仿照基于散射波动方程的散射数据偏移成像方法，利用Kirchhoff近似获得基于反射系数的反射波场的Kirchhoff积分形式表达式(即Kirchhoff积分形式的反射波场正演计算表达式)，然后以此正演表达式为基础，提出了改进的Kirchhoff积分偏移成像方法——真振幅Kirchhoff积分偏移成像方法，即对反射系数的真振幅Kirchhoff积分偏移成像方法。但是在Kirchhoff近似中对于反射面上的反射波场与入射波场间的关系表达仍然采用了类似Claerbout“时间一致性”成像公式中的表达，即ur=Rui(ur表示反射波场，R表示所定义界面的反射系数，ui表示入射波场)。为了获得波动方程(单程波方程和双程波方程)的真振幅偏移成像方法，一些研究者[55-57]根据上述的散射偏移成像方法和真振幅Kirchhoff积分偏移成像方法对Claerbout“时间一致性”成像公式进行修改，得到所谓的真振幅成像公式，并由此得到的真振幅偏移成像方法具有与真振幅Kirchhoff积分偏移成像方法相类似的真振幅特性。笔者认为仅对成像公式进行修改，对于建立波动方程真振幅偏移成像方法只是治标不治本，而应先建立与地震偏移成像对应的反射数据正演问题，再利用反演的方法构建出真正的反射数据波动方程真振幅偏移成像方法。

根据上述认识，笔者认为无论是当前以反射面位置为目标的反射数据偏移成像方法(包括基于微分方程求解的波动方程方法和基于射线追踪的Kirchhoff积分方法和束偏移成像方法)还是真振幅偏移成像方法，以及以反射体的速度相对扰动为目标的地震反射数据线性反演方法(当前的最小二乘偏移成像方法)所面临的最大问题是缺乏描述反射波传播的反射波动方程，致使不能建立基于反射波动方程的反射数据反演成像公式。在地震数据的反演成像中，如果所建立的反演成像方法不是完全基于描述波场传播的波动方程的，则该反演成像方法就不能完全利用地震数据的波形信息。由于成像公式的缘故，当前的地震数据偏移成像方法不是一种完全的波动方程方法，不能完全利用地震数据的波形信息。正演问题是进行反演的基础，为了建立完全基于反射波动方程的反射数据成像方法，需推导控制反射波传播的反射波动方程，然后在反演理论指导下建立可完全利用地震数据波形信息对反射波动方程中模型参数进行成像的波形成像方法。本文的波形成像包括波形线性反演和波形偏移。在有关波现象和地下介质物理参数空间变化的高频近似条件下，利用地震波传播的扰动理论研究描述地震反射波传播的反射波动方程，推导出基于阻抗相对扰动的反射波动方程和基于反射率变化的反射波动方程。在仅考虑一次反射波的假定下，分别利用基于阻抗相对扰动的一次反射波动方程和基于反射率的一次反射波动方程推导反演阻抗相对扰动的波形线性反演方法和反演反射率的波形偏移方法，因为反射率不仅是一种物性参数，而且其分布还指示了反射面位置，所以把反演反射率的波形线性反演称为波形偏移。在波形线性反演和波形偏移方法中都包含了利用反射波传播算子的伴随算子的近似方法和利用反射波传播算子的最小二乘逆算子的最小二乘方法。最后把所提出的反射数据波形成像方法应用于合成数据，以验证方法的正确性和有效性。

2 反射波动方程

为了构建基于反射波传播方程的反射数据波形线性反演与波形偏移方法，必须构建适合反射数据波形线性反演与波形偏移的反射波动方程，即需要建立基于物性参数相对扰动的反射波动方程和基于反射面物性参数—反射率变化的反射波动方程。散射理论及其散射波动方程是研究地震波传播的基本方法理论[58]，在有关波现象和地下介质物理性质空间变化的高频近似条件下，产生散射波的散射体可近似为反射体，相应的散射波退化为反射波。地震勘探中的地震反射波在地下运动的物理过程在直观上可表述为，地表震源激发的入射波场向下传播，与反射体作用产生反射波场，反射波场向上传播到地表被检波器接收。因此地震反射波的地下运动物理过程由波的反射和传播组成。

2.1 地震波的传播与反射

在应力与应变线性近似假定下，震源激发的地震波在地下的运动可用下述非线性微分算子方程描述

L(m)u=f

(1)

式中：L为与地下模型参数m有关的二阶偏微分算子，也称为波动算子；u为表示地震波在地下运动状态的状态变量，也称为地震波场；f为激发地震波的震源函数。式(1)也称为非齐次波动方程，或辐射方程。如果式(1)的右端项等于零(无源项)，则得到齐次波动方程，即

L(m)u=0

(2)

式(1)、式(2)能描述震源和地下模型m变化产生的各种波，如直达波、散射波、反射波、透射波和转换波(对于弹性波动方程)等，因此它们也称为通用波动方程，是地震波场模拟、地震数据全波形反演和波场外推的基础方程。在描述地震波场运动状态的通用波动方程(式(1))中，地震反射波的传播与反射是交织在一起的，这是因为式(1)中的模型参数m不仅控制了波场传播，也控制了地震波的反射。为了清楚地描述地震反射波的运动状态，根据对地震反射波传播的直观认识，希望有描述反射波场传播的微分方程和描述反射波场反射的微分方程，也就是希望能在模型m中将传播与反射分开，得到控制传播的传播模型mp和控制反射的反射模型mr，在形式上把m表示为m=mp+mr。

为了得到对传播模型mp和反射模型mr的认识，将地震波传播的散射理论应用于式(1)。即令m=mb+δm，其中mb表示背景模型，δm为模型扰动； 相应的波场有u=ub+δu，其中δu为波场扰动，ub表示背景模型下的波场。于是有

L(mb)ub=f

(3)

将上述模型和波场扰动表达代入式(1)，有

L(mb)δu=δL(mb,δm)u

(4)

式中：L(mb)为背景模型下的波动算子； 扰动波场δu也称为散射波场； δL(mb,δm)为由背景模型和扰动模型综合产生的扰动算子，也称为散射算子，有δL(mb,δm)=L(mb+δm)-L(mb)；u为与模型m对应的全波波场。式(4)也称为散射波动方程。在一阶Born近似下，对于一次散射波，可写为

L(mb)δu=δL(mb,δm)ub

(5)

在散射理论的Born近似中，对于δm不仅要求在数值上相对mb要小很多，即|δm|≪mb，而且在空间上要求是局部分布。由于地震波场是一种具有一定频带范围的波动数据，因此δm的空间局部分布要求与地震波场的波长(主频波长)大小有关。通常认为，如果δm的空间变化特征尺度小于等于主频波长，则δm可视为局部分布的散射体，产生散射波场。在高频情况下，相对于短波长，如果δm的空间局部分布要求难以满足，因而认为δm相对于短波长的地震波在空间上具有一定延续度。因此，在高频近似条件下，δm可视为反射体，散射波场退化为反射波场，相应的散射波动方程(式(4)、式(5))就退化为反射波动方程。

在光学中，所谓的反射都是镜面反射，是由镜面两侧介质的速度变化产生的[59]。在地震勘探中，地下介质主要由块状体和层状体组成。层状介质产生地震反射波，块状体的空间尺寸与地震波的波长关系决定它是产生散射波的散射体还是产生反射波的反射体。本文所讨论的地震反射是高频近似条件下对地震散射的近似，即在地震波场的波长比较短的情况时，δm的空间局部分布对于地震波可视为反射体，δm的空间变化在地震波场的波长尺度下可视为缓慢变化甚至常数，它与入射波场的作用产生反射波场。

根据上述认识，在高频近似条件下，假定背景模型mb是光滑变化，即式(3)中波场ub不包含反射波场，则地面观测到的地震反射都是由δm产生。与mb对应的波动算子L(mb)控制和描述了地震波场的传播，称之为传播算子； 与δm有关的扰动算子δL(mb,δm)控制和描述了地震波的反射，称之为反射算子。因此光滑的背景模型mb就是所谓的地震波传播模型，δm和mb共同组成了所谓的反射模型。

2.2 基于阻抗相对扰动的反射波动方程

为了体现简洁和一般性，令波动方程式(1)中的模型参数m为速度v(x)和密度ρ(x)，则式(1)可表述如下

u(x,t;xs)=f(t)δ(x-xs)

(6)

(7)

(8)

=f(t)δ(x-xs)

(9)

如果不考虑密度变化，则声波动方程式(6)就简化为标量波动方程，即

(10)

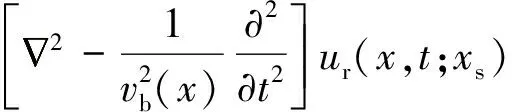
(11)

(12)

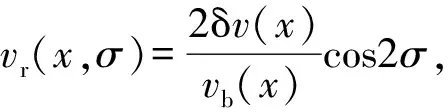
(13)

2.3 基于反射率变化的反射波动方程

(14a)

根据反射率的定义，反射率r(x,σ)也有下述定义式，即

(14b)

上述定义的反射率是一个与反射半开角σ有关的变量，是介质声波阻抗空间变化的反映。

把式(7)、式(8)变换到频率域，有频率域的基于声波阻抗相对扰动的全反射波和一次反射波的声波反射波动方程，即

(15)

(16)

把反射率定义式(14)代入方程式(15)、式(16)，可得到频率域的基于反射率变化的全反射波和一次反射波的声波反射波动方程，即

(17)

(18)

把式(17)、式(18)变换到时间域，有

(19)

(20)

式(19)、式(20)分别称为时间域的基于反射率变化的全反射波和一次反射波的声波反射波动方程。

对于标量波动方程式(10)，为了得到基于反射面上反射率变化的反射波动方程，定义地下反射率为速度相对扰动vr(x,σ)沿入射波传播方向I的方向导数，即

(21)

利用定义式(21)，由基于速度相对扰动的标量反射波动方程式(11)、式(12)，通过与上述相类似的推导，可得到时间域的基于反射率变化的全反射波和一次反射波的标量反射波动方程，即

(22)

(23)

上述的反射波动方程都是在高频近似条件下推导出来的，反射波动方程中的波场是高频近似下的局部平面波场。

3 反射数据的波形成像

在高频近似条件下得到的全反射波和一次反射波的反射波动(式(7)和式(8)、式(11)和式(12)、式(19)和式(20)、式(22)和式(23))是进行全反射波和一次反射波模拟和反演成像的基础方程。对于一次反射波的模拟，给定震源函数、光滑的背景模型和阻抗(速度)相对扰动或反射面上的反射率，利用推导出的一次反射波动方程(式(8)、式(12)、式(20)和式(23))就可实现对一次反射波场的数值模拟。对于一次反射波的反演成像，给定地震一次反射数据、震源函数和光滑的背景模型，利用推导出的一次反射波动方程(式(8)、式(12)、式(20)和式(23))就可实现对阻抗(速度)相对扰动或反射面上反射率的反演成像。

基于反射波动方程构建的地震反射数据反演成像方法可有效利用反射波形信息，正如基于波动方程构建的地震数据全波形反演方法一般可有效地利用地震数据的波形信息。一次反射波动方程是关于阻抗(速度)相对扰动或反射率的线性方程。根据一次波反射波动方程，利用地震一次反射数据对阻抗(速度)相对扰动或反射率进行成像是线性反演问题求解。将这种完全根据反射波动方程可利用反射数据波形信息对阻抗(速度)相对扰动和反射率进行反演的方法分别称为地震反射数据的阻抗(速度)相对扰动波形线性反演方法和反射率波形偏移方法。依据波形线性反演中具体求解方式的不同，对于波形线性反演又分为基于反射波传播算子的伴随算子的近似反演和基于反射波传播算子的最小二乘逆算子的最小二乘反演；同样，对于波形偏移也分为基于反射波传播算子的伴随算子的波形偏移和基于反射波传播算子的最小二乘逆算子的最小二乘波形偏移。由于反射波传播算子的时空变化特征，反射波传播算子不是一个酉算子，其伴随算子不等于其逆算子，因此基于伴随算子的波形线性反演与波形偏移实质是对阻抗(速度)相对扰动和反射率的近似反演。不同于当前基于Claerbout成像原理的地震反射数据偏移方法，地震反射数据波形偏移是一种完全波动方程方法，它不仅可实现对反射面位置的成像，也可对反射面的物性参数反射率进行近似估计，最小二乘波形偏移是波形偏移的发展，是对反射面反射率的最小二乘反演。

3.1 阻抗相对扰动的近似反演与最小二乘反演

对于式(8)所表示的基于阻抗相对扰动的一次反射波动方程，借助背景模型下的Green函数可写为下述积分形式

(24)

式中：“*”代表时间褶积；g(x,t;y)为背景模型下的Green函数，有

=δ(t)δ(x-y)

(25)

把式(24)变换到频率域，有

(26)

令

(27)

其中

(28)

且F(ω)为震源函数的频谱。

把式(27)代入式(26)，并根据陈生昌等[60]提出的时间二阶积分波场的全波形反演方法，式(26)可写为

(29)

对于线性积分方程(式(29))可写为下述矩阵方程形式

u=Wm

(30)

m=W-gu=(W*W)-1W*u

(31)

式中：W-g代表W的最小二乘广义逆矩阵；W*为W的伴随矩阵。式(31)的运算在实质上是对波场数据u的最小二乘逆传播。

(32)

式中Re表示取实部。

考虑到式(31)计算的稳定性和逆矩阵计算的复杂度，可用伴随矩阵W*代替式(31)中的最小二乘广义逆矩阵W-g，有

ma=W*u

(33)

式(33)的运算在实质上是对波场数据u的伴随传播(逆时传播)。

再考虑式(32)中波场相除运算的不稳定性问题，并结合式(33)，把式(32)改写为

(34)

式中上标“*”代表复共轭运算。用式(34)代替式(32)，虽然可以保证计算的稳定性和减小计算的复杂度，但会造成反演结果的保真性变差、分辨率降低。

式(28)、式(33)和式(34)所表示的运算构成了对阻抗相对变化Ir(x,σ)的近似反演。把对Ir(x,σ)的近似反演运算转换到时间域，就有：

(1)地下入射波场的计算(对应式(28)所表示的运算)

=f(t)δ(x-xs)

(35)

(2)地下时间二次积分反射波场的伴随(逆时)重建(对应式(33)所表示的运算)

(36)

(3)对阻抗相对变化Ir(x,σ)的近似反演(对应式(34)所表示的运算)

(37)

(38)

利用基于速度相对扰动的标量波反射波动方程(式(12))和相类似的公式推导，可得到对速度相对变化vr(x,σ)的近似反演，其相应的计算公式为如下。

(1)地下入射波场的计算

(39)

(2)地下时间二次积分反射波场的伴随(逆时)重建

(40)

(3)对速度相对变化vr(x,σ)的近似反演

(41a)

或写成

(41b)

式(41a)、式(41b)得到的速度相对变化近似反演结果可以用来估计速度扰动。

由于式(33)、式(34)中的近似，致使上述的波形偏移方法会受到地震数据观测系统、地下介质变化、地震波几何扩散以及近似反演公式等对成像结果的分辨率、信噪比和保真性产生的不利影响，所得到的结果对是对阻抗(速度)相对变化的近似估计。

显然，式(28)、式(31)和式(32)虽然在理论上给出了利用最小二乘反演阻抗相对变化的计算公式，可以得到一个高分辨率、高信噪比和高保真性的阻抗(速度)相对变化估计，但存在一些数值计算方面的难题： 一是式(31)右端中的逆矩阵(W*W)-1的大规模计算问题和它的不稳定性问题； 二是式(32)右端中的波场相除运算也会出现计算的不稳定问题。

(42)

Δuik=ui-Wmk

(43)

Δmik=W*Δuik

(44)

(45)

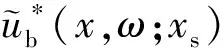
利用迭代所得到的有关阻抗相对变化的反演，即称之为基于波场最小二乘逆传播的反演，也称为阻抗相对扰动的最小二乘反演。

(46)

Δuik=ui-Wmk

(47)

Δmik=W*Δuik

(48)

(49)

利用迭代所得到的有关速度相对变化的反演，称之为基于波场最小二乘逆传播的反演，也称为速度相对扰动的最小二乘反演。

通过迭代方式的最小二乘反演得到的相对波阻抗(速度)扰动相对于近似反演得到的相对波阻抗(速度)扰动具有保真性好、分辨率高，但相应的计算量会大量增加。

3.2 反射率的波形偏移与最小二乘波形偏移

根据基于反射率变化的一次波反射波动方程(式(20))，利用地震一次反射数据，不仅可对反射面位置进行成像，即实现对反射面位置的偏移成像，还能对反射面的物性参数反射率进行估计。对于式(20)所表示的一次反射波动方程借助Green函数可写为积分形式，有

(50)

采用与地震反射数据的阻抗相对扰动近似反演相类似的公式推导，得到下列基于波场伴随传播的对反射率r(x,σ)进行近似估计的波形偏移时间域计算公式。

(1)地下入射波场的计算

=f(t)δ(x-xs)

(51)

(2)地下反射波场的伴随(逆时)重建

(52)

(3)对反射率r(x,σ)的近似估计

(53)

式(52)中的dr(x,t;xs)为共炮道集地震反射数据；式(53)中的波场ur(x,t;xs)的时间一阶导数对获得高分辨率的r(x,σ)波形偏移结果有帮助。

根据标量波一次反射波动方程(式(23))，利用波场的伴随传播运算和相应的公式推导，得到下列对r(x,σ)进行近似估计的波形偏移时间域计算公式。

(1)地下入射波场的计算

(54)

(2)地下反射波场的伴随(逆时)重建

(55)

(3)对反射率r(x,σ)的近似估计

(56)

上述导出的波形偏移成像方法不同于当前基于Claerbout成像原理的波动方程逆时偏移成像方法，它是一种基于反射波动方程的反演方法，不需要应用所谓的偏移成像原理及其成像公式，能够在波动方程意义下真实地应用地震数据的波形信息，是一种真正的波动方程偏移成像方法。

(57)

Δuk=u-Wmk

(58)

Δmk=W*Δuk

(59)

rk+1(x,σ)=rk(x,σ)+αρb(x)vb(x)×

(60)

上述迭代所得到的有关反射率的波形偏移，可称之为基于波场最小二乘逆传播的波形偏移，也称为反射率的最小二乘波形偏移。

(61)

Δuk=u-Wmk

(62)

Δmk=W*Δuk

(63)

rk+1(x,σ)=rk(x,σ)+αvb(x)×

(64)

迭代方式的最小二乘波形偏移得到的反射率相对于波形偏移得到的反射率具有保真性好、分辨率高的优点，但相应地计算量会大量增加。当前的最小二乘逆时偏移方法得到的是阻抗(速度)的相对扰动，而不是逆时偏移方法所得到的反射面位置，对于缺少低频信息和高频信息的带限地震数据，最小二乘逆时偏移得到的是阻抗(速度)的相对扰动不能清晰地刻画反射面的位置，即当前的最小二乘逆时偏移结果与逆时偏移结果是不同的。最小二乘逆时偏移不是对反射面位置的成像，因此严格地说最小二乘逆时偏移不是偏移，而本文提出的最小二乘波形偏移与波形偏移都是对反射面反射率的成像。

根据地下非均匀体的体积大小和波阻抗变化快慢与地震波长之间的相对关系，把非均匀体划分为产生散射波的散射体和产生反射波的反射体，然后在高频近似条件下推导出两种不同参数的反射波方程，即基于波阻抗相对扰动的反射波方程和基于反射率的反射波方程，并把它们分别作为反射数据的正演方程。本文认为对于散射波和反射波应有不同的散射波方程和反射波方程，相应地对于散射数据和反射数据也应有不同的散射数据波形成像方法和反射数据波形成像方法[63]，但当前的偏移成像中不区分散射和反射。为了更精细地实现对地下目标的成像，趋向认为在偏移成像中对于散射波和反射波应有不同的方法。本文波形成像方法的目标是产生反射数据的反射体和反射面。如果波形成像的目标是产生散射数据的散射体，就需要应用基于散射波方程的散射数据波形成像方法。本文认为在地震数据的成像中，为了得到高分辨、高保真的成像结果，对于散射数据和反射数据应该区别对待，使用不同的方法。根据相关经验，基于反射波方程的反射数据波形成像方法对于散射体产生的散射数据也能进行成像，只是成像效果不如基于散射波方程的散射数据波形成像方法的。同样，基于散射波方程的散射数据波形成像方法对于反射体产生的反射数据也能进行成像，只是成像效果不如基于反射波方程的反射数据波形成像方法的。

4 数值试验

为了验证上文所提出的地震反射数据波形成像方法的正确性和有效性，采用不考虑密度变化的标量波合成地震反射数据进行了速度相对扰动的近似反演、反射率的波形偏移和最小二乘波形偏移试验。

4.1 速度相对扰动的近似反演试验

为了验证所提出的速度相对扰动近似反演方法的正确性和有效性，本文构建了如图1a所示的字母模型，该模型包含2层，上部低速层速度为2500m/s，下部高速度层速度为3000m/s，在上部的低速层中含有6个速度为2750m/s的高速字母体。利用标量波动方程(式(10))的有限差分方法进行合成地震数据模拟。在本试验总共模拟了501炮，炮间距为40m，为中间放炮两边接收，每炮1001道，道间距为20m，时间采样间隔是4ms，时间采样点数为1250，震源为主频20Hz的Ricker子波。这些字母体相对于主频波长可视为反射体，因此合成得到的地震数据是反射波数据。图1b为用于近似反演试验的光滑速度模型，它是通过对图1a的速度模型进行光滑处理得到的。图1c为图1a所示的真实速度模型与图1b所示的光滑速度模型之间的速度扰动。图1d为利用本文提出的速度相对扰动近似反演方法得到的速度相对扰动近似反演结果。对比图1c、图1d可看出，近似反演得到的速度扰动结果相对于理论速度扰动虽然存在保真性和分辨率方面的不足，但是反演的速度扰动与理论速度扰动有相同的变化形态。该试验结果验证了本文所提出的速度相对扰动近似反演方法的正确性和有效性。

图1 速度相对扰动的近似反演效果(a)字母模型的速度模型； (b)光滑的背景速度模型； (c)图a与图b之间的速度扰动； (d)近似反演得到的速度扰动

4.2 反射率的波形偏移试验

为了验证所提出的反射率波形偏移方法的正确性和有效性，对两套合成数据进行了波形偏移试验，第1个是上述字母模型数据的试验，第2个是Sigbee2A模型数据的试验。

4.2.1 字母模型数据的试验

利用上节得到的字母模型的反射数据和图1b所示的光滑背景速度模型，分别应用常规逆时偏移成像方法和本文提出的波形偏移成像方法对字母模型进行偏移成像。图2a为常规逆时偏移的结果，图2b为波形偏移的结果。图3为图1c所示字母模型真实速度与背景速度之间速度扰动的垂向反射率。对比图2a、图2b和图1a模型可看出，逆时偏移方法和本文的波形偏移方法虽然都能对字母体边界和速度分界面进行很好的成像，但逆时偏移得到的结果有90°的相位差，即分界面处于波峰与波谷的过渡带上，图2a逆时偏移结果的分辨率也不如图2b波形偏移结果的高。对比图2b和图3可看出，波形偏移方法可以很好地对字母体边界和速度分界面上的反射率进行成像，波形偏移得到的反射率与图3中的垂向理论反射率有相同的极性和相位。逆时偏移和波形偏移都在浅部反射面上方出现了低频噪声，试验中虽然用Laplace滤波方法进行了压制，但还有较明显残余。由于波形成像方法与逆时偏移相比多了对震源波场的时间一阶导数，因此其低频噪声相对于逆时偏移更强，为了减弱低频噪声对波形成像结果多做一次Laplace滤波，所以造成成像能量的相对减弱，使直立90°边界成像看起来不如逆时偏移的结果。深部出现的噪声主要是用于逆时偏移和波形偏移的光滑速度模型与真实速度模型的偏差引起的。由于伴随传播和反射率近似估计公式(式(56))，致使反射率波形偏移结果的分辨率和保真性受到不利影响。

图2 常规逆时偏移(a)和波形偏移(b)结果

图3 模型速度扰动的理论垂向反射率

4.2.2 Sigbee2A模型数据的试验

Sigbee2A模型含有高速盐体、精细的反射面。图4a是用于偏移成像试验的背景速度模型。模型尺寸为3201×1201个网格点，水平和垂直方向的网格间距均为7.62m，该模拟数据的观测系统为海上拖缆观测系统。该地震数据含有500炮，炮间距为45.72m，拖缆长度为7932.42m，检波点间距为22.86m，每一炮的道数不均，最少为57道，最多为348道，时间采样间隔为8ms，时间采样点数为1500。

分别应用常规逆时偏移成像方法和本文提出的波形偏移成像方法对Sigbee2A模型数据进行偏移成像。图4b和图4c分别为常规逆时偏移成像结果和波形偏移成像结果。对比图4b和图4c可见，虽然两种偏移成像方法都能对Sigbee2A模型进行很好的成像，但本文提出的波形偏移的结果相对于逆时偏移的结果有更高的分辨率，因为波形偏移结果中反射界面的同相轴相对更细。本文的方法虽然是针对反射体(面)产生的反射数据进行成像，但对于盐体边界上的角点和模型中的点散射体产生的绕射波和散射波也能进行很好的成像，而且所得到的成像结果也好于常规的逆时偏移。为了获得更精细的成像结果，建议若成像目标是产生反射数据的反射体(面)，就采用基于反射波动方程建立的反射数据波形成像方法； 若成像目标是产生散射数据的散射体，就采用基于反射波动方程建立的反射数据波形成像方法。

图4 针对Sigbee2A背景速度模型(a)的常规逆时偏移(b)和波形偏移(c)结果

图5 部分Sigsbee2a模型的波形偏移结果、最小二乘波形偏移结果和理论垂向反射率

(a)部分Sigsbee2a模型的速度分布； (b)用于偏移的光滑速度模型； (c)波形偏移结果； (d)35次迭代的最小二乘波形偏移结果； (e)模型速度扰动的理论垂向反射率

上述两个试验的结果验证了本文所提出的波形偏移成像方法的正确性和有效性，以及该方法相对于常规逆时偏移成像方法的优势。

4.3 反射率的最小二乘波形偏移试验

为了验证反射率最小二乘波形偏移方法的正确性和有效性，截取Sigsbee2a速度模型的一部分进行试验，如图5a所示。利用标量波动方程式(10)的有限差分方法进行合成地震数据模拟。在本试验总共模拟了300炮，炮点范围是0～6km，炮间距为20m，为中间放炮两边接收，每炮601道，道间距为10m，时间采样间隔是0.5ms，时间采样点数为3000，震源为主频18Hz的Ricker子波。图5b为用于最小二乘波形偏移试验的光滑速度模型，它同样是通过对图5a的速度模型进行光滑处理得到的。

在试验中，首先应用提出的反射波动方程波形偏移方法对合成的炮道集地震数据进行波形偏移成像，图5c为利用波形偏移方法得到的偏移成像结果。由图5c可看出，波形偏移方法对该模型可获得很好的偏移成像结果。图5d为应用本文提出的反射波动方程最小二乘波形偏移成像方法对部分Sigsbee2a模型的偏移成像结果，共进行了35次迭代。对比图5c与图5d可看出，最小二乘波形偏移结果的分辨率相对于波形偏移结果的有明显地提高，而且层位面与断层面的成像更清晰。与图5e所示的部分Sigsbee2a模型的垂向理论反射率对比可看出图5d的最小二乘波形偏移结果的振幅保真性相对图5c的波形偏移结果也有明显的提高。

上述模型数据的数值试验结果验证了本文所提出的最小二乘波形偏移成像方法的正确性和有效性。由于缺乏实际数据和研究条件的限制，本文所提出的方法没有进行实际数据的测试。根据前文的计算公式， 认为本文所提出的方法具有很强的实用性，因为本文所提出的方法计算过程与当前的逆时偏移和最小二乘逆时偏移相同，所不同的只是成像公式。

5 结论

根据地震数据所满足的波动方程进行反演成像的求解可充分利用地震数据的波形信息。基于阻抗相对扰动的反射波动方程和基于反射率的反射波动方程分别是阻抗相对扰动反演和反射率波形偏移的正演问题。地震一次反射数据的阻抗相对扰动反演和反射率的波形偏移都属于波形线性反演。利用反射波传播算子的伴随算子所构建的近似反演和波形偏移方法虽然可对阻抗相对扰动和反射率进行成像，但保幅性、分辨率和信噪比存在不足；利用反射波传播算子的最小二乘算子所构建的最小二乘反演和最小二乘波形偏移方法虽然计算量增大(至少增加一个量级的计算量)，但成像结果的保幅性、分辨率和信噪比会有明显提高。本文所提出的波形偏移成像方法是一种真正的波动方程方法，不需要应用成像原理及其成像公式。本文的波形成像方法不仅可以实现地下介质参数构造成像，还能进行物性成像，是对当前地震数据偏移成像方法的升级换代。合成数据的数值试验结果验证了本文所提出的波形成像方法的正确性和有效性。本文所提出的波形偏移方法与当前的逆时偏移方法的计算过程一致，不会增加计算量，适用条件也一样。本文从数学物理正反演的角度对地震反射数据的偏移成像进行了重新定义和推导，使得到的偏移成像结果具有明确的数学物理意义，可为后续偏移成像结果的进一步应用(如基于角度域成像道集的AVA分析和岩性反演)提供基础。

参考文献

[1] Lailly P．The seismic inverse problem as a sequence of before stack migrations．Conference Expanded Abstracts on Inverse Scattering，Theory and Application，Society for Industrial and Applied Mathematics，1983，206-220.

[2] Tarantola A．Inversion of seismic reflection data in the acoustic approximation．Geophysics，1984，49(8)：1259-1266.

[3] Tarantola A．Linearized inversion of seismic reflection data.Geophysical Prospecting,1984,32(4)：998-1015.

[4] Gray S，Etgen J，Dellinger J et al．Seismic migration problems and solutions．Geophysics，2001，66(5)：1622-1640.

[5] Yilmaz O．Seismic Data Analysis．SEG，2001.

[6] Etgen J，Gray S，Zhang Y．An overview of depth imaging in exploration geophysics．Geophysics，2009，74(6)：WCA5-WCA17.

[7] Leveille J，Jones I，Zhou Z et al．Subsalt imaging for exploration，production，and development：A review．Geophysics，2011，76(5)：WB3-WB20.

[8] Claerbout J．Toward a unified theory of reflector mapping．Geophysics，1971，36(3)：467-481.

[9] Claerbout J．Fundamentals of Geophysical Data Processing．McGraw-Hill Book Co Inc，1976.

[10] Claerbout J．Imaging of the Earth’s Interior．Blackwell Scientific Publication，1985.

[11] Loewenthal D，Lu L，Roberson R et al．The wave equation applied to migration．Geophysical Prospecting，1976，24(2)：380-399.

[12] 马在田．地震成像技术：有限差分偏移．北京：石油工业出版社，1989.

[13] Robein E．Seismic imaging：A review of the techniques，their principles，merits and limitations．EAGE，2010.

[14] Stolt R，Benson A．Seismic Migration：Theory and Practice．Geophysical Press，London，1986.

[15] Bleistein N，Cohen J，Stockwell J．Mathematics of Multi-dimensional Seismic Imaging，Migration，and Inversion． Springer， New York，2001.

[16] 李振春等编著．地震叠前成像理论与方法．山东东营：中国石油大学出版社，2011.

[17] 李振春．地震偏移成像技术研究现状与发展趋势．石油地球物理勘探，2014，49(1)：1-21．

Li Zhenchun．Research status and development trends for seismic migration technology．OGP，2014，49(1)：1-21.

[18] Du Q， Zhu Y， Ba J．Polarity reversal correction for elastic reverse time migration．Geophysics，2012，77(2)：S31-S41.

[19] Chang W，McMechan G．A 3-D elastic prestack reverse-time depth migration．Geophysics，1994，59(4)：597-609.

[20] Zhang Y，Duan L and Xie Y．A stable and practical implementation of least-squares reverse time migration．Geophysics，2014，80(1)：V23-V31.

[21] Yao G，Jakubowicz H．Least-squares reverse time migration．SEG Technical Program Expanded Abstracts，2012，31：1-5.

[22] Yao G，Jakubowicz H．Non-linear least-squares reverse time migration．SEG Technical Program Expanded Abstracts，2012，31：1-5.

[23] Dong S，Cai J，Guo M et al．Least-squares reverse time migration：towards true amplitude imaging and impoving the resolution．SEG Technical Program Expanded Abstracts，2012，31：1-5.

[24] Gray S．True-amplitude seismic migration：A comparison of three approaches．Geophysics，1997，62(3)：926-936.

[25] 郭振波，李振春．最小平方逆时偏移真振幅成像．石油地球物理勘探，2014，49(1)：113-120．

Guo Zhenbo，Li Zhenchun．True amplitude imaging based on least-squares reverse time migration．OGP，2014，49(1)：113-120.

[26] 黄建平，孙陨松，李振春等．一种基于分频编码的最小二乘裂步偏移方法．石油地球物理勘探，2014，49(4)：702-707.

Huang Jianping，Sun Yunsong，Li Zhenchun et al．Least-squares split step migration based on frequency division encoding．OGP，2014，49(4)：702-709.

[27] 周华敏，陈生昌，任浩然等．基于照明补偿的单程波最小二乘偏移．地球物理学报，2014，57(8)：2644-2655．

Zhou Huamin，Chen Shengchang，Ren Haoran et al．One way wave equation least squares migration based on illumination compensation．Chinese Journal of Geophysics，2014，57(8)：2644-2655.

[28] Zhang Y，Ratcliffe A，Duan L．Velocity and impedance inversion based on true amplitude reverse time migration．SEG Technical Program Expanded Abstracts， 2013，32： 949-953.

[29] Duan L，Zhang Y and Peng L．Band-limited impedance perturbation inversion using cross-correlative least-squares RTM．SEG Technical Program Expanded Abstracts，2014，33：3720-3725.

[30] Berkhout A．Seismic Migration：Imaging of Acoustic Energy by Wavefield Extrapolation，Part A：Theoretical Aspects(2nd Ed).Elsevier，1982.

[31] Gazdag J．Wave equation migration with the phase-shift method．Geophysics，1978， 43(7)：1342-1351.

[32] Berkhout A．Steep-dip finite-difference migration.Geophysics，1979，44(1)：196-213.

[33] Huang L，Wu R．Prestack depth migration with acoustic screen propagators．SEG Technical Program Expanded Abstracts，1996，15：415-418.

[34] Ristow D，Ruhl T．Fourier finite-difference migration．Geophysics，1994，59(12)：1882-1893.

[35] Chen J，Liu H．Two kinds of separable approxima-tions for the one-way wave operator．Geophysics，2006，71(1)：T1-T5.

[36] 陈生昌，马在田，Wu Rushan．波动方程偏移成像阴影的照明补偿．地球物理学报，2007，50(3)：844-850．

Chen Shengchang，Ma Zaitian，Wu Rushan．Illumination compensation for wave equation migration shadow．Chinese Journal of Geophysics，2007，50(3)：844-850.

[37] 刘少勇，韩冰凯，顾汉明等．带限局部平面波传播算子与偏移方法．石油地球物理勘探，2017，52(5)：948-955．

Liu Shaoyong，Han Bingkai，Gu Hanming et al．Band-limited local plane wave propagator and migration．OGP，2017，52(5)：948-955.

[38] Hemon C．Wave equations and models．Geophysical Prospecting，1978，26(4)：790-821.

[39] McMechan G．Migration by extrapolation of time-dependent boundary values．Geophysical Prospecting，1983，31(3)：413-420.

[40] Baysal E，Kosloff D and Sherwood J．Reverse time migration．Geophysics，1983，48(11)：1514-1524.

[41] Whitmore D．Iterative depth migration by backward time propagation．SEG Technical Program Expanded Abstracts，1983，2：382-385.

[42] French W．Two-dimensional and three-dimensional migration of model-experiment reflection．Geophy-sics，1974，39(1)：265-277.

[43] Schneider W．Integral formulation for migration in two and three dimensions．Geophysics，1978，43(1)：49-76.

[44] Sun J．Limited aperture migration．Geophysics，2000，65(2)：584-595.

[45] Cerveny V，Popov M and Psencilk I．Computation of wave fields in inhomogeneous media Gaussian beam approach．Geophysical Journal of the Royal Astronomical Society，1982，70(1)：109-128.

[46] Costa C，Raz S and Kosloff D．Gaussian beam migration．SEG Technical Program Expanded Abstracts，1989，8：1169-1171.

[47] Hill N．Prestack Gaussian-beam depth migration．Geo-physics，2001，66(4)：1240-1250.

[48] Tang Y，Biondi B．Least-squares migration/inversion of blended data．SEG Technical Program Expanded Abstracts，2009，28：2859-2863.

[49] Ren H，Wu R and Wang H．Wave equation least square imaging using the local angular Hessian for amplitude correction．Geophysical Prospecting，2011，59(4)：651-661.

[50] 黄建平，李振春，孔雪等．碳酸盐岩裂缝型储层最小二乘偏移成像方法研究．地球物理学报，2013，56(5)：1716-1725．

Huang Jianping，Li Zhenchun，Kong Xue et al．A study of least squares migration method for fractured type carbonate reservoir．Chinese Journal of Geophy-sics，2013，56(5)：1716-1725.

[51] 李庆洋，黄建平，李振春等．优化的多震源最小二乘逆时偏移．石油地球物理勘探，2016，51(2)：334-341．

Li Qingyang，Huang Jianping，Li Zhenchun et al．Optimized multi-source least-squares reverse time migration．OGP，2016，51(2)：334-341.

[52] 李娜．基于Huber范数的多震源最小二乘逆时偏移．石油地球物理勘探，2017，52(5)：941-947．

Li Na．Multi-source least-squares reverse time migration based on Huber norm．OGP，2017，52(5)：941-947.

[53] Beylkin G．Imaging of discontinuities in the inverse scattering problem by the inversion of a causal Radon transform．Journal Mathematics Physics，1985，26(1)：99-108.

[54] Bleistein N．On the imaging of reflectors in the earth．Geophysics，1987，52(7)：931-942.

[55] Zhang Y，Zhang G，Bleistein N．Theory of true amplitude one-way wave equation and true amplitude common-shot migration．SEG Technical Program Expanded Abstracts，2003，22：925-928.

[56] Xu S，Zhang Y，Tang B．3D angle gathers from reverse time migration．Geophysics，2011，76(2)：S77-S92.

[57] Duprat V，Baina R．Prestack true amplitude imaging condition．SEG Technical Program Expanded Abstracts，2015，34：4075-4079.

[58] Devaney J．Mathematical Foundations of Imaging，Tomography and Wavefield Inversion．Cambridge University Press，2012.

[59] Goodman J．Introduction to Fourier Optics(3rd Ed).Roberts and Company Publishers Inc，2005.

[60] 陈生昌，陈国新．时间二阶积分波场的全波形反演．地球物理学报，2016，59(10)：3765-3776．

Chen Shengchang，Chen Guoxin．Full waveform inversion of the second-order time integral wavefield．Chinese Journal of Geophysics，2016，59(10)：3765-3776.

[61] Sava P， Fomel S．Angle-domain common-image ga-thers by wavefield continuation methods．Geophy-sics，2003，68(3)：1065-1074.

[62] Kirsch A．An Introduction to the Mathematical Theory of Inverse Problems(2nd Ed).Springer，2011.

[63] 陈生昌，周华敏．再论地震数据偏移成像．地球物理学报，2016，59(2)：643-65．

Chen Shengchang，Zhou Huamin．Re-exploration to migration of seismic data．Chinese Journal of Geophysics，2016，59(2)：643-654．