关于Burgers方程在L∞模下收敛的差分格式
朱 玲,徐维艳,孙 红
(江苏科技大学 理学院, 镇江 212003)
Burgers方程是一个重要的和普遍的非线性模型,在等离子物理、量子场论、非线性光学和通信技术等领域有着重要的地位和作用. Burgers方程是一个双曲—抛物型非线性微分方程,描述物理问题的对流和耗散的综合过程, 兼有一阶波动方程和热传导方程的特性. 应用有限差分方法研究Burgers方程主要分为两大类:一是当源项f=0时,对Burgers方程作Cole-Holf变换,将其转换成经典的热方程,再对变换后的热方程建立有限差分格式.文献[1-4]中基于Cole-Holf变换对Burgers方程建立的差分格式. 二是当f≠0时,Cole-Holf变换就失效了, 需要用其他数值格式来求解[5-10].目前,对于Burgers方程的差分格式的理论分析相对较少,特别是在L∞模下的稳定性及收敛性分析更少. 文中对Burgers方程建立一个三层的线性化的差分格式,并给出了L∞模下严格的收敛性分析,考虑Burgers方程
式中,φ(x)为给定的光滑函数,且φ(0)=0,φ(1)=0.
1 记号和引理


设vh={u|u=(u0,u1,…,um),u0=um=0}是定义在Ωh上的网格函数空间, 对∀u,v∈vh, 定义内积和范数:
引理1[9]对任意的网格函数v∈Vh, 有:
引理2[9]对任意的网格函数v∈Vh, 有:
2 差分格式的建立
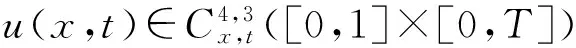
及

(4)
且存在常数c1,使得:
在点(xi,tk)处考虑方程式(2), 由Taylor展开,有:
1≤i≤m-1, 1≤k≤n-1
(5)
且存在c2,使得:
注意到初边值条件,有:
(6)
(7)
略去式(4、5)中的小量项, 对式(1~3)可建立差分格式:
对于格式中的ut(xi,0)可以利用方程式(1)和初值条件式(2)求得:
ut(xi,0)=φxx(xi)-φ(xi)φx(xi)+f(xi,0)
3 差分格式的唯一可解性和收敛性

‖ek‖∞≤C(τ2+h2) 0≤k≤n
(16)
证明: 应用数学归纳法证明此定理.
当k=0,由式(14~15), 有:
|e0|1=0, ‖e0‖=0
因此,结论对k=0是成立的.
首先:证明u1是由式(8、11)唯一确定,且式(16)对k=1是成立的.
(1) 考虑式(8、11)的齐次方程组, 有:

于是有:


因而, 方程组(8,11)唯一确定u1.
则:



由上面的不等式可得:
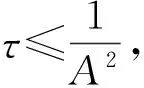
(19)
应用引理1, 得:
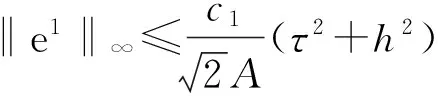
因此,式(16)对k=1是成立的.
其次,假设式(8~11)唯一确定uk(1≤k≤l),且式(16)对1≤k≤l是成立的. 下面将证明ul+1可由式(8~11)唯一确定且式(16)对k=l+1是成立的.

‖ek‖∞≤1, 1≤k≤l
因此,
‖uk‖∞≤‖Uk‖∞+‖ek‖∞≤1+c01≤k≤l
(20)
式(21)两边同时与ul+1作内积, 得:
(23)
应用引理2, 可得:
(24)
由Cauchy-Schwarz不等式和式(20), 有:
(25)
将式(24、25)代入式(23), 得到:
(26)

于是,ul+1由式(8~11)唯一确定.
(2) 证明式(16)对k=l+1是成立的.
式(13)与Δtek作内积, 可得:
由引理1.2, 有:
注意到,
于是,
1≤k≤l
(27)
由Cauchy-Schwarz不等式, 引理1和式(20), 得:

和
将以上两个不等式代入式(27), 得:
于是有:
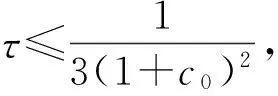
于是,

h2)2,1≤k≤l
应用Gronwall不等式和式(19), 得:
由上面的不等式, 可得:
|el+1|1≤c3(τ2+h2)

由引理1, 有:
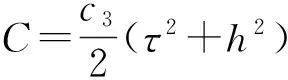
因此,式(16)对k=l+1也是成立的,定理证毕.
4 数值试验
应用差分格式(8~11)来计算一个例子,验证文中建立的差分格式的精度和有效性.
例: 设T=1,f(x,t)=e-tsin(πx)(-1+
πe-tcos(πx)+π2),且φ(x)=sin(πx),问题(1~3)有精确解u(x,t)=sin(πx)e-t.
记最大模误差:
时间方向的收敛阶定义为order1=log2(E∞(
h,2τ)/E∞(h,τ)),当h足够小.
空间方向的收敛阶定义为order2=log2(E∞(
2h,τ)/E∞(h,τ)),当τ足够小.
定义order3=log2(E∞(2h,2τ)/E∞(h,τ)) 为差分格式的收敛阶.

表1 当h=1/800时,时间方向的最大模下的误差和收敛阶Table 1 Maximum norm errors and the temporalconvergence orders with h=1/800
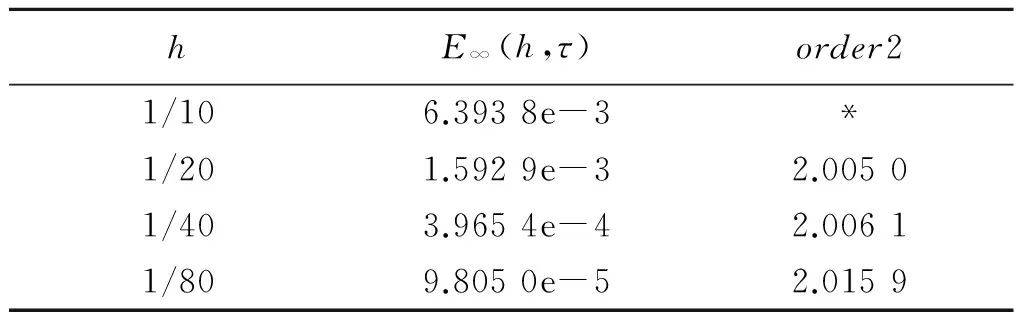
表2 当τ=1/1 000时,空间方向的最大模下的误差和收敛阶Table 2 Maximum norm errors and the spatialconvergence orders with τ=1/1000

表3 差分格式的最大模误差和收敛阶Table 3 Maximum norm errors andconvergence orders
从表1~3可以看出,差分格式(8~11)在时间和空间方向上的收敛阶都是二阶的, 与文中的理论结果相吻合.
5 结论
对Buegers方程建立了一个三层线性化的差分格式, 并应用离散能量法和数学归纳法对所建立的差分格式的唯一可解性和在最大模意义下的收敛性给出了严格的理论证明, 数值试验验证了理论结果.
参考文献(References)
[ 1 ] KADALBAJOO M K, AWASTHI A. A numerical method based on Crank-Nicolson scheme for Burgers′ equation[J]. Appl Math Comput, 2006(182):1430-1442.
[ 2 ] LIAO W. An implicit fourth-order compact finite difference scheme for one-dimensional Burgers′ equation[J]. Applied Mathematics and Computation, 2008(2): 755-764. DOI:10.1016/j.amc.2008.09.037.
[ 3 ] PANDEY K, VERMA L, VERMA A K. On a finite difference scheme for Burgers′ equation[J]. Applied Mathematics and Computation, 2009(6): 2206-2214. DOI:10.1016/j.amc.2009.08.018.
[ 4 ] XIE S, LI G, YI S, et al. A compact finite difference method for solving Burgers′ equation[J]. International Journal for Numerical Methods in Fluids, 2010, 62(7):747-764.
[ 5 ] 郭本瑜. Burgers方程的数值解(Ⅰ)[J]. 高等学校计算数学学报, 1982(2):51-66.
GUO B. Numerical solution of Burgers equation (I)[J]. Numerical Mathematis A Journal of Chinese Universities,1982(2):51-66.(in Chinese)
[ 6 ] SARI M, GÜRARSLAN G. A sixth-order compact finite difference scheme to the numerical solutions of Burgers′ equation[J]. Applied Mathematics and Computation, 2009(2): 475-483. DOI:10.1016/j.amc.2008.12.012.
[ 7 ] 田强, 赵国忠. Burgers方程的指数型差分格式[J]. 内蒙古大学学报(自然科学版), 2009, 40(1): 37-41.
TIANG Q, ZHAO G. Exponential finite difference scheme for Burgers equation[J]. Journal of Inner Mongolia University(Natural Science Edition),2009,40:37-41.(in Chinese)
[ 8 ] 谢焕田. Burgers方程差分解的收敛性与稳定性[J]. 高校应用数学学报A辑, 2012, 27(1): 57-62.
XIE H T. Finite difference schemes for Burgers′ equation[J]. Appled Mathematics A Journal Chinese Universities,2012,27(1):57-62.(in Chinese)
[ 9 ] 孙志忠, 偏微分方程数值解法[M].2版.北京:科学出版社, 2012.
[10] REFIK B A. Numerical solution for one-dimensional Burgers′ equation using a fully implicit finite-difference method[J]. Int J Appl Math, 1999(8): 897-909.
[11] SUN H, SUN Z Z. On two linearized difference schemes for Burgers′ equation[J]. International Journal of Computer Mathematics, 2015, 92(6):1160-1179.

