基于PSO算法的空间映射方法设计微波滤波器

许 兰,田雨波,高国栋,陈 艺

(江苏科技大学 电子信息学院,镇江 212003)

传统的微波滤波器设计主要依据等效解析式,但解析式有其局限性,需依靠后期调试来提高滤波器的性能．虽然高频仿真软件可以优化其性能,但如果滤波器的结构相对复杂,优化变量比较多时,就很难得到理想效果,而且相当耗时．文献[1]提出了一种新型的电磁快速优化计算方法——空间映射方法，其核心思想是将主要的优化计算工作放到以粗糙模型为基础的替代模型中进行,而采用精确模型进行验证工作,充分利用了精确模型的准确性和粗糙模型的高效性．文献[2-3]分别提出了主动空间映射方法和隐式空间映射方法，以及随后相继提出的自适应空间映射方法[4]和改进算法[5-7]，都在不断改善精确模型与设计目标的逼近速度．目前,空间映射方法已经成功设计了微波滤波器、天线、功分器等微波器件[8-9]．

由于传统的空间映射方法,其参数提取过程需要在粗糙空间通过优化完成,耗时很长．将粒子群优化算法(particle swarm optimization,PSO)[10]与空间映射方法相结合[11]，参数提取过程由PSO优化算法与粗糙模型结合而成的替代模型来完成，此提取过程只需简单的四则运算,计算复杂度大大减小,耗费时间也减少,从而提高了参数提取的速度．文中通过设计平行耦合滤波器对该方法进行验证，结果显示算法有效．

1 基于PSO算法的空间映射方法

1.1 算法原理

在空间映射算法中,用两种模型来描述具体的微波电路,其中能够准确而全面的反应出模型的实际特性但耗时较长的模型称为精确模型,其设计变量为xf,响应为Rf(xf);而仿真快速高效但精确度相对不高的模型称为粗糙模型,其设计变量为xc,响应为Rc(xc)．可以作为粗糙模型的有：等效电路模型、数学解析表达式或者粗糙网格模型．

定义待求解问题为:

(1)

空间映射算法假定粗糙模型设计变量xc与精细模型设计变量xf存在映射关系:

xc=P(xf)

(2)

并在一定范围内使得:

Rc(P(xf))≈Rf(xf)

(3)

参数提取是空间映射算法中的关键步骤,其目的是在粗糙空间中找到点xc,使得:

(4)

粒子群优化算法是一种智能优化算法[12]，其思想来源于自然界中的鸟类捕食,与蚁群算法类似，都有群智能的特点．PSO算法是求解域的直接迭代优化算法,算法参数少,易于实现,具备较强的收敛和全局搜索能力,因此发展十分迅速,在诸多领域得到了成功应用[13-14]．

文中将PSO优化算法与空间映射方法中的粗糙模型结合成为替代模型,其中PSO算法的初始种群通过粗糙模型获得,精确模型在Ansoft HFSS中建立,用来验证新的设计参数是否满足设计目标,满足即算法结束,不满足则通过PSO优化器进行更新；并将新的设计参数在精确模型中验证,判断所得结果是否趋优,如果不是,返回至原位置,如此循环直到满足设计目标,算法结束．算法基本流程如图1．

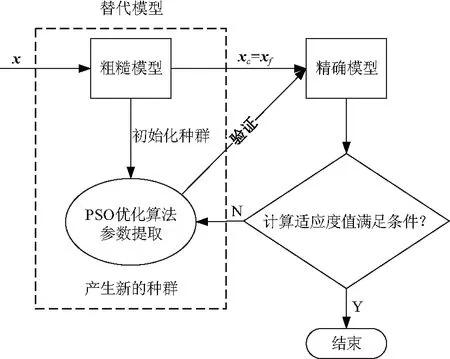
图1 基于PSO算法的空间映射方法的基本流程Fig.1 Basic flow of the space-mapping based on PSO

(5)

式中：i为粒子编号,k为某粒子的迭代次数,g为频点个数,f(j)为频率,wj为对应于f(j)的权重系数．式(5)中

(6)

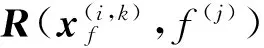
(7)

最优粒子的适应度是最小的,若设置的求解粒子适应度的标准比设计目标更加严格时,可以更快达到设计目标,但此时可能达不到算法停止标准,因此，通过调节最大优化次数来进行控制,选择全局最优粒子．

1.2 参数提取过程

参数提取是空间映射方法的关键步骤,目的是获得更接近优化目标的设计参数．文中所提算法是通过PSO优化算法调整当前粒子的位置来获得新的种群粒子．这种参数提取过程是非常简单四则运算,可以大大缩短参数提取的时间．速度更新方程(也就是参数提取过程)为:

v(h+1)=ωv(h)+c1rand()(pbest(h)-x(h))+

c2rand()(gbest(h)-x(h))

(8)

粒子更新公式:

x(h+1)=xh+v(h+1)

(9)

式中：h=m*(k-1)+i,m为初始种群大小,pbest(h)为单个粒子的个体极值位置；gbest(h)是全体粒子的全局极值的位置；pbest(h)和gbest(h)是根据每个粒子的适应度选取而得到的．ω为惯性权重,c1和c2为学习因子或加速常数,rand()是介于(0,1)的随机数．这里的ω取0.9,c1=c2=1.3．需要说明一点,在计算适应度的过程中最好粒子的适应度值最小且总不小于零．

文中算法是通过粒子更新公式获得新的粒子x(h+1),并在精确空间Xf中进行验证，然后计算新的粒子适应度值,并判断其是否满足停止标准,满足即算法结束,否则继续迭代,直到找到满足设计目标的最优设计参数．算法流程如图2．

图2 设计方法流程Fig.2 Flow chart of the method

1.3 算法实现过程

由于粗糙模型在Agilent ADS中建立,精确模型在Ansoft HFSS中建立,因此采用MATLAB程序控制Agilent ADS和Ansoft HFSS来实现基于PSO算法的空间映射方法．通过在建立精确模型的过程中记录HFSS API脚本,然后在MATLAB使用fprintf()函数产生HFSS API脚本来实现MATLAB对Ansoft HFSS的调用．MATLAB调用Agilent ADS相对比较复杂一点,通过fprintf()函数编写AEL脚本控制Agilent ADS,但AEL并不是很智能,在执行仿真指令时不会等待仿真结束再跳转至下一指令,导致结果读取就不成功．所以在粗糙模型建立时加入控件MeasEqn,并使用write-var函数将仿真结果写入标志仿真结束的识别文件中,其目的就是在仿真结束后能在指定目录中产生识别文件,然后在AEL脚本中加入一个判断识别文件是否存在,是否需要等待的过程,确保仿真结束后再执行下一语句．特别说明的是,write-var函数不支持多数据,当要写入识别文件的数据是多维数组时需要添加[0,::]．

除了通过编写AEL脚本和使用fprintf()函数以外,在MATLAB主控制程序中产生AEL脚本函数的后面要添加如下语句:

system(’ADS安装路径 —m脚本文件路径’)．

2 平行耦合带通滤波器例证

文中通过平行耦合带通滤波器证明算法的有效性,设计指标如表1，滤波器结构如图3．在Agilent ADS中建立平行耦合带通滤波器的粗糙模型并根据设计指标获取初始种群,在Ansoft HFSS中建立其精确模型．带通滤波器的性能与微带线的长L,微带线的宽W以及间隔S有关,将这些参数定为设计参数[L1L2L3W1W2W3S1S2S3]．

表1 平行耦合带通滤波器设计指标Table 1 Design index of parallel-coupled bandpass filter

本例中的固定不变参数有端口微带线长L0=17.2 mm,宽W0=0.84 mm,端口微带线边缘与介质基板边缘距离S0=2.5 mm．设定介质基板厚度H=0.5 mm,微带线厚度T=0.005 mm,相对介电常数Er=3.66．图4为其精确模型图，图5为其粗糙模型图．

图3 平行耦合带通滤波器的结构Fig.3 Structure of parallel-coupled bandpass filter

图4 平行耦合带通滤波器的精确模型Fig.4 Fine model of parallel-coupled bandpass filter

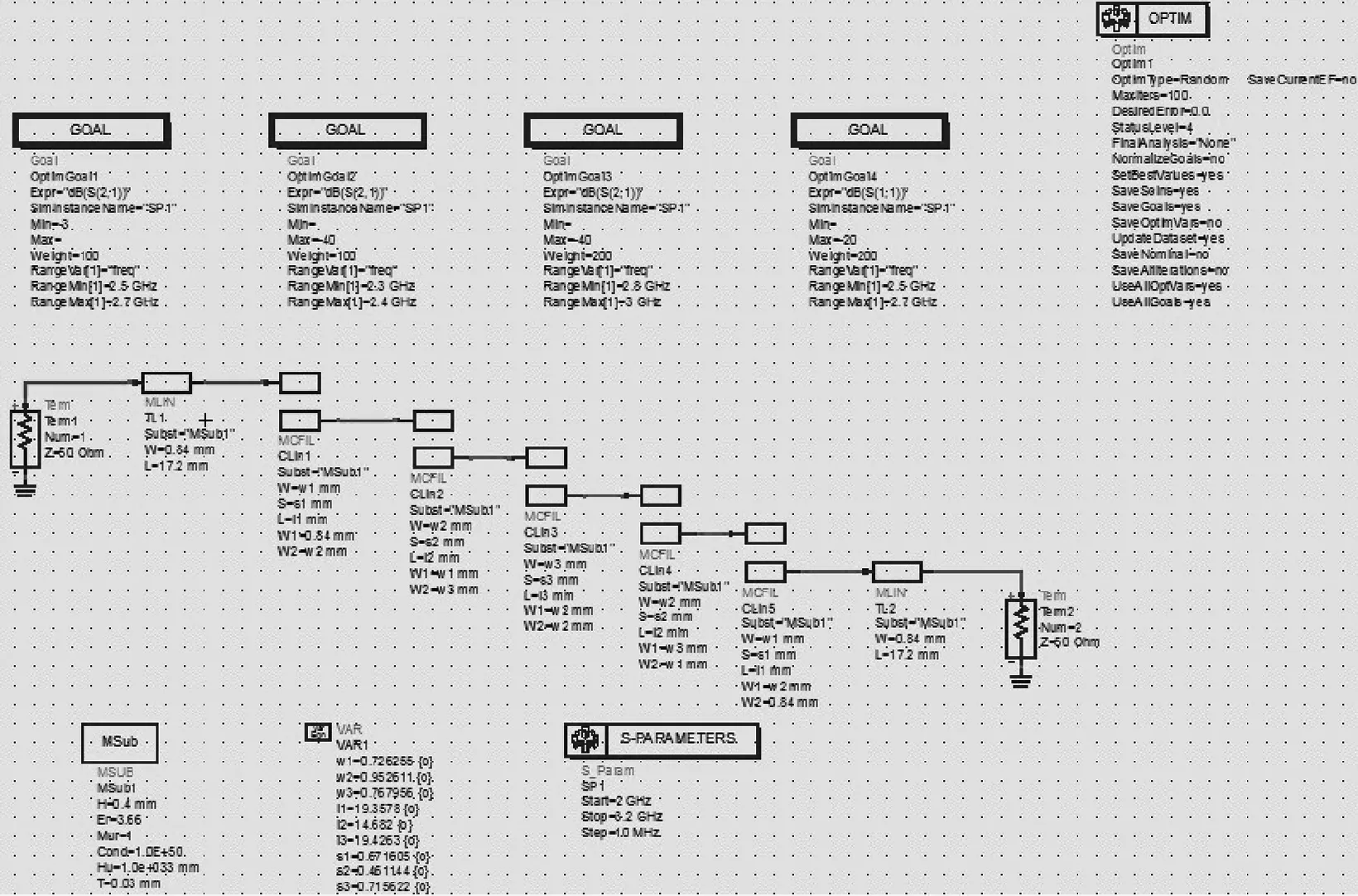
图5 平行耦合带通滤波器的粗糙模型Fig.5 Coarse model of parallel-coupled bandpass filter

算法首先设置不同的起点作为PSO初始种群，并在ADS中进行优化,大小为5，然而将所得的粗糙模型参数带入HFSS中进行验证,计算每个粒子的适应度．计算适应度时,需根据指标添加相对应的权重系数．其中一个粒子的验证结果如图6,可以明显看出结果并不满足设计指标,此时进入下一循环,通过PSO优化算法进行参数提取产生新的粒子．在此过程中设置判断所产生的新的粒子是否向好的方向发展,如果是,则算法继续,如果不是,则返回上一粒子的位置,并将其作为新的起点,然后在HFSS中进行验证,如此循环,直到达到目标,算法结束．

图7(a)为第一次优化迭代后的最优的精确模型响应,可以看到带宽已达目标,但在mark4处的带外抑制和mark6处的回波损耗未达标;图7(b)为第二次优化迭代后的最优的精确模型响应,基本达到设计目标,只是mark4处的带外抑制还差一点;图7(c)为第三次优化迭代后的最优的精确模型响应,可以看出与设计目标相符．最优设计参数为:

图6 未使用优化算法时滤波器的初始响应Fig.6 Initial fine model respondingwithout using the method

图7 不同优化次数时最优精确模型响应Fig.7 Fine model responding of different generation

实验结果验证了基于PSO算法的空间映射方法的有效性．

3 结论

在传统主动空间映射方法基础上,结合PSO算法实现了算法设计．基于PSO算法的空间映射方法相当于将主动空间映射方法中的拟牛顿迭代的过程改进为PSO算法的四则运算，其优势是参数提取过程变得非常简单,无需考虑复杂的梯度问题,大大缩短了参数提取时间．通过微带滤波器的仿真实例说明了算法的有效性．

参考文献(References)

[ 1 ] BANDLER J W, BIERNACKI R M, CHEN S H, et al. Space mapping technique for electromagnetic optimization [J]. IEEE Transactions on Microwave Theory and Techniques, 1994, 42(12): 2536-2544.

[ 2 ] BANDLER J W, BIERNACKI R M, CHEN S H, et al. Electromagnetic optimization exploiting aggressive space mapping[J]. IEEE Transactions on Microwave Theory and Techniques, 1995(12): 2874-2882. DOI:10.1109/22.475649.

[ 3 ] BANDLER J W, CHENG Q S, NIKOLOVA N K, et al. Implicit space mapping optimization exploiting preassigned parameters[J]. IEEE Transactions on Microwave Theory and Techniques, 2004, 52(1): 378-385. DOI:10.1109/tmtt.2003.820892.

[ 4 ] CHENG Q S, BANDLER J W, KOZIEL S. Tuning space mapping optimization exploiting embedded surrogate elements[J]. 2009 IEEE MTT-S International Microwave Symposium Digest, 2009, 3(5):1257-1260. DOI:10.1109/mwsym.2009.5165932.

[ 5 ] 朱永忠, 岳亮. 置信区间渐进空间映射算法优化设计共形微带天线[J]. 苏州大学学报(自然科学版),2011, 27(3):42-45.

ZHU Yongzhong, YUE Liang. Design and optimization of conformal microstrip antenna with trust region aggressive space mapping[J].Journal of Soochow University(Natural Science Edition),2011,27(3):42-45.(in Chinese)

[ 6 ] 邢连发, 雷振亚, 谢拥军，等. 新型高收敛隐式空间映射算法设计微波滤波器[J]. 电子与信息学报, 2011, 33(3):744-748.

XING Lianfa, LEI Zhenya, XIE Yongjun, et al. A new implicit space mapping with high convergence for microwave filter design[J]. Journal of Electronics & Information Technology, 2011, 33(3):744-748.(in Chinese)

[ 7 ] 张永亮, 苏涛, 吴边,等. 基于矢量拟合与渐进空间映射的微波滤波器调试[J]. 华南理工大学学报(自然科学版),2013,41(2):19-23.

ZHANG Yongliang, SU Tao, WU Bian, et al. Tuning of microwave filters based on vector fitting and aggressive space mapping[J]. Journal of South China University of Technology(Natural Science Edition),2013,41(2):19-23.(in Chinese)

[ 8 ] 罗璇. 基于空间映射方法的微波滤波器优化设计[D]. 南京理工大学, 2013:14-52.

[ 9 ] 吴召海, 谢拥军, 樊君,等. 空间映射算法优化共形天线阵方向图特性[J]. 电子器件, 2010, 33(2):201-204.

WU Zhaohai, XIE Yongjun,FAN Jun, et al. Optimization of the radiation pattern of conformal antenna arry by space mapping algorithm[J]. Chinese Journal of Electron Devices, 2010, 33(2):201-204.(in Chinese)

[10] KENNEDY J, EBERHART R. Particle swarm optimization [C]∥IEEE International Conference on Neural Networks.Perth,WA,Australia:IEEE，2002,4(8):1942-1948. DOI:10.1109/icnn.1995.488968.

[11] 毋俊玱. 空间映射方法研究及其在微波电路中的应用[D].电子科技大学, 2013:16-35.

[12] 田雨波, 陈风, 张贞凯. 混合神经网络技术[M].2版. 北京: 科学出版社, 2015:94-125.

[13] 田雨波, 沙莎, 彭涛. 蝶形单元电磁带隙结构粒子群优化设计研究[J]. 电波科学学报, 2011, 26(1):133-138.

[14] 田雨波.粒子群优化算法及电磁应用[M]. 北京: 科学出版社, 2014: 179-188.

[15] 陈艺，车久菊，田雨波.基于ADS的KBNN在带通滤波器优化设计中的研究[J].江苏科技大学学报(自然科学版)，2018，32(1)：83-87.DOI:10.3969/j.issn.1673-4807.2018.01.016.

CHEN Yi,CHE Jiuju,TIAN Yubo.ADS-based KBNN to optimize the band-pass filter[J].Journal of Jiangsu University of Science and Technology(Natural Science Edition),2018,32(1):83-87.DOI:10.3969/j.issn.1673-4807.2018.01.016.(in Chinese)