基于知识转化，探求以题会类— —以如何证明线段相等为例

☉上海市岭南中学 刘华为

习题教学虽然切入角度多种多样，操作形式也千变万化（如一题多解、一题多变和多题归一等），但就其目标而言，除了巩固知识外主要还是培养学生的解题能力和完善学生的思维方式.因此，如何弃“量”从“精”，切实减轻学生过重的作业负担，全面提升学生分析问题的能力便成了习题教学的主旋律和一种高境界的追求.对此笔者的体会有两点：一是以“怎么想到这样做”为切入点，借助知识溯源丰富解题分析的转化策略，从而教会学生“转化”；二是以“同一类型还可怎么做”为抓手，借“知识迁移”拓宽处理同类问题的解题技巧，从而教会学生“类化”.现以“如何证明线段相等”为例作一操作示范解读，以求抛砖引玉.

一、从对一道经典几何题解法的深度思考谈如何教会学生转化

例1 如图1，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，求证：BD=CD.

本题常规的辅助线添法如图2所示，分别过D、C作DE⊥BC于点E，CF⊥AD于点F，易证△CDE≌△CDF，得所以DE垂直平分BC，故BD=CD.

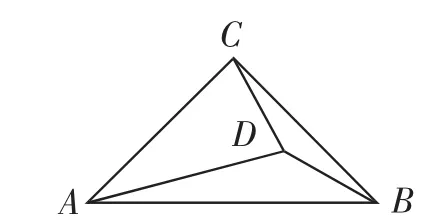
图1

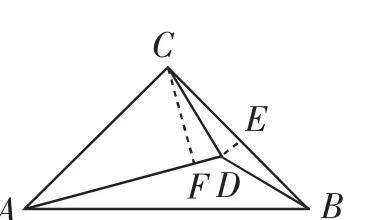
图2

思考1：怎么想到这样添辅助线？

事实上，就转化思想而言，所有数学问题都是运用所学过的知识来求解的，而这些解决相关问题的知识点通常称之为“知识源”，也是解决同类问题的致胜法宝.如本题属于证明线段相等问题，而回顾初中阶段所学过的与“证明线段相等”有关的知识源主要有“线段中点的定义（知识源1）”“全等三角形对应边相等（知识源2）”“等角对等边（知识源3）”“中垂线的性质（知识源4）”“角平分线上任意一点到角的两边距离相等（知识源5）”“平行四边形对边相等（知识源6）”“平行线等分线段定理（含三角形与梯形的中位线定理）（知识源7）和“同弧（或等弧）所对的弦及弦的弦心距相等（知识源8）”等，本题结合条件与图形的特征易想到运用知识源2、3、4处理.

若用知识源“中垂线的性质”证明，自然想到过点D作DE⊥BC于点E，再证明CE=BE=（当然也可取BC的中点E，连接DE证明DE⊥BC），注意到AC=BC和∠CAD=30°，由“30°角所对的直角边等于斜边的一半”想到过点C作CF⊥AD于点F（也可过点D作DG⊥AC于点G，如图3），下面只需证明CE=CF（即证明△CDE≌△CDF）即可.由条件可得∠ACD=75°且∠ACF=60°，所以∠DCE=∠DCF=15°. 又∠CED=∠CFD=90°且CD=CD，故两三角形全等，问题得证.

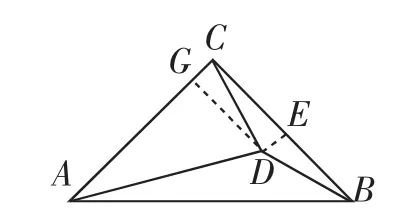
图3

图4

思考2：能否用知识源“等角对等边”证明？

由BD和CD同为△BCD的两条边自然想到用知识源“等角对等边”加以证明，又易知∠BCD=15°，所以只需证明∠CBD=15°或∠ABD=30°即可.

对于求15°的非特殊角∠CBD而言，不妨从方程思想入手，即设∠CBD=x，则∠ABD=45°-x，若再找到（或构造）∠ABD的等角，也用含x的代数式表示，便可列方程求出x的值.由∠BAD=∠BCD=15°和AD=CB想到在AB上截取AE=CD（如图4），则△ADE≌△CBD，得DE=BD且∠ADE=∠CBD=x，所以∠DEB=∠DBE，即15°+x=45°-x，解得x=15°，问题得证.

对于求30°的特殊角∠ABD而言，自然联想到构造等边三角形转化.如图5，构造等边△ABM，连接MC，由AC=BC和AM=BM 可知MC垂直平分AB，则∠AMC=30°.根据“边角边”定理易证△ABD≌△AMC，得∠ABD=∠AMC，进而得∠CBD=15°=∠BCD，所以BD=CD.

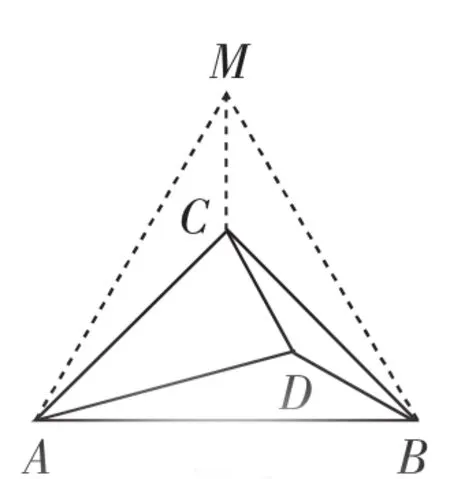
图5

图6

思考3：能否运用知识源“全等三角形对应边相等”证明？

显然图中含有线段BD和CD的现有三角形均不全等，需重新构造.不妨以CD所在的△ACD为目标三角形，由∠ACB=90°想到过点B作BN⊥BC且BN=AC（如图6），连接DN，则△NBD必与△ACD全等，只是不易证明.然而连接AN后可惊奇地发现四边形ACBN为正方形，故不妨反其道而行之，直接构造正方形ACBN，连接DN，则证明△ACD≌△NBD就易如反掌了.

若以BD所在的△ABD为目标三角形，则可把△ABD沿AD翻折得△APD（如图7），不过在证明CD=PD（即△CDP为等边三角形）时遇到障碍.也可反其道而行之，先构造等边△CDP，连接AP交CD于点O，再证明△PAD≌△BAD.由AC=AD和CP=DP知AP垂直平分线段CD，则∠PAD==15°=∠BAD，则问题转化为证明AP=AB.注意到△ABC为等腰直角三角形、△CDP为等边三角形和△ACD是顶角为30°的等腰三角形，故可通

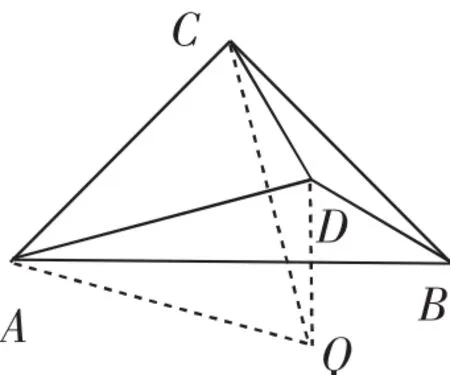
图8

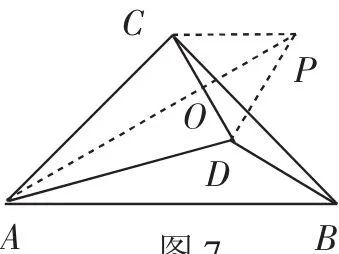
图7

当然也可以△CBD为目标三角形构造全等三角形，不妨把△CBD沿CD翻折得△CQD（如图8），连接AQ，易证△ACQ为等边三角形，进而得△ACD≌△AQD，所以CD=QD=BD.

思考4：如何引导学生学会转化（即学会“怎样想”）？

其实，对于上述分析笔者通常称之为“知识溯源式目标分析法”，主要有三步：首先要明确解题目标是什么，如例1的终极目标是证明两条线段相等；其次，根据目标追溯与其相关的知识源，如回顾初中阶段所学知识发现与证明线段相等的知识主要有8个（见上）；最后，根据条件结合知识源的主要特征选择适合的知识源求解，如上述解法就是根据例1的条件和图形特征选择了知识源2、知识源3和知识源4而生成的.教学中，若能从学法指导角度入手，以“知识溯源式目标分析法”为抓手，以上述三步为操作模式，逐步引导学生学会“怎样想”，丰富转化策略，必然能极大地减少解题的盲目性，全面提升解决问题的能力.

二、借助“同一类型还可怎么做”教会学生类化

显然，例1主要是借助知识源“中垂线的性质”“等角对等边”和“全等三角形对应边相等”处理的，那么在什么情况下又分别运用其他知识源处理呢？

1.利用知识源“线段中点的定义”证明

例2如图9，在△ABC中，AB⊥AC，AD⊥BC于点D，E，F分别是边AB，AC上一点，且DE⊥DF.若△ABC的中位线MN交EF于点H，求证：EH=FH.

思路分析：从EH与FH的位置特征，自然想到运用知识源“线段中点的定义”证明EH=FH.若点H为EF的中点，注意到∠EAF与∠FDE为直角，所以A、E、D、F四点共圆，且EF为直径，所以点H必为圆心.而由MN是△ABC的中位线和AD⊥BC可知，MN垂直平分弦AD，所以MN必经过圆心，则MN与直径EF的交点H就是圆心，故EH=FH.

2.利用知识源“角平分线上任意一点到角的两边距离相等”证明

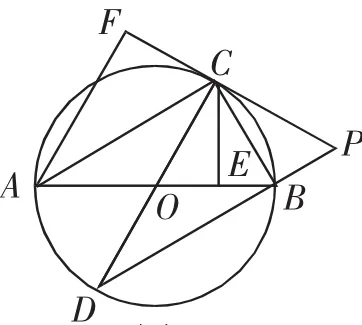
图10

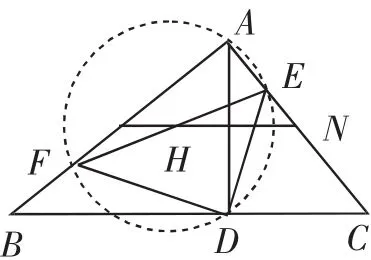
图9

例3（2017年广东中考题）如图10，AB是⊙O的直径，，，点E为线段OB上一点（不与点O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连接CB.

（1）求证：CB是∠ECP的平分线；

（2）求证：CF=CE；

思路分析：（1）略（.2）从CF⊥AF和CE⊥AB的特征可知，欲证CF=CE只需证明AC平分∠EAF.由CF为⊙O的切线可知，∠ACF=∠ABC.又∠ACF+∠CAF=90°且∠ABC+∠CAB=90°，所以∠CAF=∠CAB，问题得证（.3）过点B作BQ⊥CP于点Q，不妨设CF=3t，CP=4t，则CQ=CE=CF=3t且

3.利用知识源“平行四边形对边相等”证明

例4（2017年温州中考题）如图11，在△ABC中，AC=BC，∠ACB=90°，⊙O（圆心O在△ABC内部）经过B，C两点，交AB于点E，过点E作⊙O的切线交AC于点F.延长CO交AB于点G，作ED∥AC交CG于点D.

（1）求证：DE=CF；

（2）若BC=3，tan∠DEF=2，求BG的值.

思路分析：（1）由ED∥AC知要证DE=CF，只需证明四边形CDEF为平行四边形即EF∥CD即可.由EF为⊙O的切线想到连接OE，得∠FEO=90°，则问题转化为证明∠EOC=90°，即∠OEC=∠OCE=45°.而由弦切角的性质知∠CEF=∠B=45°，所以∠OCE=∠OEC=∠CEF=45°，得EF∥CD，问题迎刃而解（.2）过G作GM⊥BC于M，可得∠FCD=∠FED=∠CGM，所以CM=2GM=2BM，得BG=

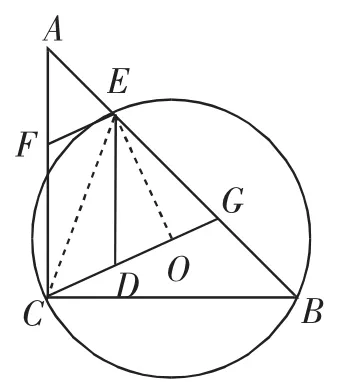
图11

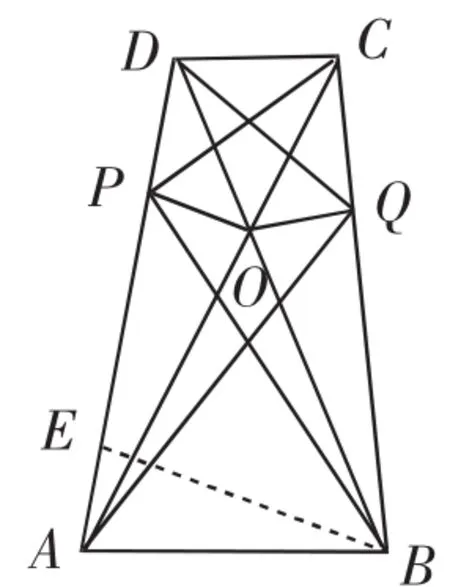
图12

4.利用知识源“比例式”等量转化

例5（2012年全国初中数学联赛试题）如图12，梯形ABCD中，AB∥CD，AC，BD相交于点O.P，Q分别是AD，BC上的点，且∠APB=∠CPD，∠AQB=∠CQD.求证：OP＝OQ.

思路分析：虽然由OP与OQ的位置特征，易联想到连接PQ用知识源“等角对等边”证明，但是不易证明∠OPQ=∠OQP.于是由∠APB=∠CPD和∠AQB=∠CQD想到构造相似三角形，再结合AB∥CD，不妨考虑用比例

5.利用知识源“同弧或等弧所对的弦相等”证明

例6（2017年江汉中考题）如图13，AB为⊙O的直径，C为⊙O上一点，AD与过点C的切线互相垂直，垂足为点D，AD交⊙O于点E，连接CE，CB.

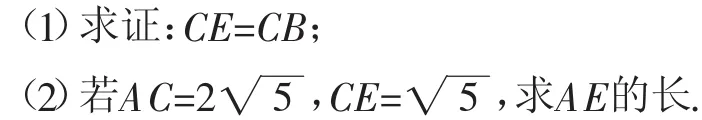
思路分析：（1）由CE与CB是⊙O的两条弦想到可证明CE=CB，即证明∠CAE=∠CAB.由弦切角的性质可知∠ACD=∠B，又∠ACD+∠CAE=90°且∠B+∠CAB=90°，所以∠CAE=∠CAB，问题得证（.2）由CB=CE=、AC=得AB=5.再由△ABC∽△ACD及其对应边成比例得DC=2，根据勾股定理可得AD=4，DE=，所以AE=

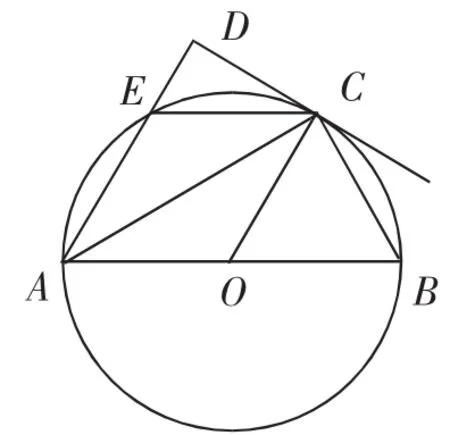
图13

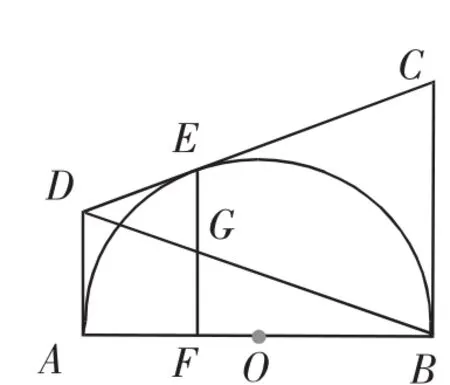
图14

6.运用计算法证明线段相等

例7（2012年宿迁中考题）如图14，在四边形ABCD中，∠DAB=∠ABC=90°，CD与以AB为直径的半圆相切于点E，EF⊥AB于点F，EF交BD于点G，设AD=a，BC=b.

（1）求CD的长度（用a，b表示）；

（2）求EG的长度（用a，b表示）；

（3）试判断EG与FG是否相等，并说明理由.

思路分析：（1）a+b，（2）略；（3）由EG和FG的位置特征易想到运用知识源“线段中点的定义”证明，不过直接证明G为EF的中点并不容易，由（2）想到不妨再求出FG，

当然，证明两线相等的转化策略远非以上几种，只要我们做个有心人，平时多注重积累就一定能在“以题会类”上有更多的作为，从而为减轻学生过重的学习负担尽善尽美.不管怎样，笔者认为习题教学务必要做到三个“坚持”：坚持以知识溯源为思路引领，明确思考方向；坚持以“教会学生怎么想”为能力抓手，强化学法指导；坚持以“同一类型还可怎么做”为拓展方向，力求“以题会类”.另外，通过以上分析也不难看出，从“知识溯源式目标分析法”入手，详细剖析辅助线的生成过程，引导学生不仅知道“怎样做”，还学会“怎样想”.其积极意义在于：基于知识转化的核心思想之下，把致力于培养学生思维分析能力和知识迁移能力的习题教学宗旨真正落到实处，为日后遇到新问题适时迁移（即以题会类）奠定扎实的基础，注重了发展性学力的培养.H