运用有效策略，实现数学思维显性化*——以运用方程（组）解决实际问题为例

☉江苏南京市江宁区周岗学校 徐 亮

☉江苏南京市竹山中学 黄秀旺

在初中数学应用题教学中，学生往往因为生活阅历有限，对应用题的背景和情境不熟，主观认为应用题很难理解，从而影响了正常的数学思维，导致应用题无法解决.应用题解题的关键在于如何找出题中的数量关系，从而根据数量关系列出符合题意的方程（组）、不等式和函数关系式，这是学生对应用题畏惧心理的根源所在，而初中应用题题型的单一性，决定了解题中列式的难度并不大.笔者通过实践，发现在用方程（组）解决实际问题的教学中，通过灵活运用以下几种策略辅助分析，可为厘清题目中数量关系，将学生的数学思维显性化，提供有效的帮助.

一、以关键词为突破，实现数量关系的显性化

小学阶段的应用题是在文字题的基础上结合具体的问题情境架构而成的，学生对解决文字题，把握关键词的做法有着丰富的经验积累.初中阶段的应用题，题中经常会出现数量关系的关键字词提示，教师只要通过合理的问题进行引导，就能让学生很明了地厘清题中的数量关系，列方程（组）也就水到渠成.

例1（2017年徐州中考第24题）2017年4月9日上午8时，2017徐州国际马拉松赛鸣枪开跑，一名34岁的男子带着他的两个孩子一同参加了比赛，下面是两个孩子与记者的对话：

根据对话的内容，请你用方程的知识帮记者求出哥哥和妹妹的年龄.

分析：解决本题的关键就是对两个数量关系式的提取，而其中的两个关键词就是解决此题的突破口，即妹妹所说的“和”，哥哥所说的“相加”，教师围绕这两个关键词合理的设问引导，此题即可迎刃而解.

师：题中哪些关键字词揭示了爸爸、哥哥、妹妹年龄之间的关系？

生：妹妹口中的“和”与哥哥口中的“相加”.

师：根据这两个关键词可以列出怎样的数量关系式？

生：①妹妹的年龄＋哥哥的年龄＝16；

②两年后妹妹年龄的3倍＋两年后哥哥的年龄＝两年后爸爸的年龄.

师：哪些量是已知的，哪些量是未知的？

生：已知爸爸今年的年龄34岁，两年后是（34+2）＝36岁，妹妹和哥哥的年龄是未知的.

师：很好，这里有两个未知量，那我们该如何求解呢？

生：因为有两个未知量，所以我们可以设妹妹今年的年龄是x岁，哥哥今年的年龄是y岁，列出方程组求解.

……

学生解决方程类的应用题，从小学起就积累的良好的知识基础.常见的题型及题型中的数量关系都是耳熟能详的，教师在教学中只要引导学生把握题中的关键词，诸如和、差、倍、分、增加、减少、扩大、缩小，等等.以关键词作为解题突破的策略，结合基本题型的理解，排除问题情境中无关文字的干扰，应用题中各数量间的关系就可以自然地显性呈现.数量关系式一目了然，转化为方程求解也就顺理成章.

二、以表格为手段，实现对应关系的显性化

对于数量关系阐述不明显的应用题，特别是营销类问题、工程类问题等，学生如果不能很好地把握数量间的对应关系和变化特征，就会对题目中各数量之间关系的理解产生混乱，此时可以从基本的数量关系入手，引导学生借助表格，逐次呈现变化前和变化后的各个数量，让对应关系显性化，从而列出方程.

例2某商店的一种服装，每件成本为50元.经市场调研，售价为60元时，可销售800件；售价每提高5元，销售量将减少100件.已知商店销售这批服装获利12 000元，问这种服装每件售价是多少元？

分析：一元二次方程应用中的常见问题，其基本的数量关系是：总利润＝单件利润×销售数量，关键是通过对“每…每…”的理解，确定涨价后的单件利润和降价后的数量.根据增加数量与涨价的对应关系，构造方程求解.

师：商品盈利问题中的基本数量关系是什么？

生：总利润＝单件利润×销售数量.

师：销售数量的变化受什么影响？影响的对应关系是怎样的？

生：受涨价的影响，每涨5元，销售量将减少100件.

师：若设售价为x元，则涨了多少元？销售量又减少了多少件呢？

生：先求出涨的价钱为（x－60）元，再除以5，数量即

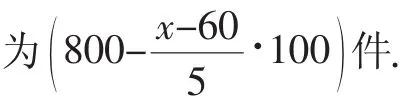
（这里的对应关系，有很多同学是不能清楚地表达的，教师可以引导学生借助表格，将数量与涨价之间的对应关系显性化，从而清晰呈现数量与价钱之间的对应关系）

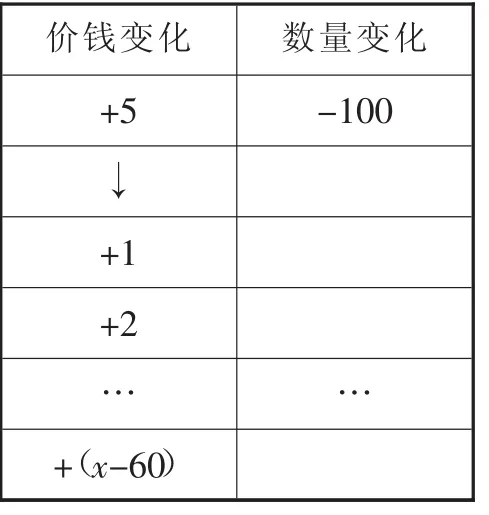
师：你能根据对应关系填写以上表格吗？

生：可以根据数量与价格间的对应关系填写.

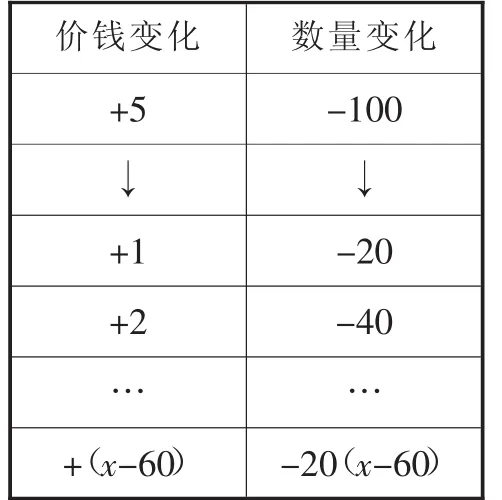
师：那根据销售这批服装获利12000元，如何求解？

生：涨价后的单件利润×涨价后的数量＝12000.

……

对于信息量大、数据繁多、对应关系复杂的应用题，借助表格手段，可以将题中数量关系和对应关系清晰地呈现.表格可以根据题型中的基本数量关系进行设计，也可以针对题中的主要对应关系设计，借助表格策略，实现复杂对应关系的显性化，在学生解决工程问题、营销问题等方面有着显著的作用.

三、以图形为辅助，实现抽象概括的显性化

有些应用题文字叙述比较精练，数量关系比较抽象.受理解能力的局限，学生对于这一类题理解起来困难较大.如果一味地从字面去分析题意，用语言来表述数量关系，往往学生有“只可意会，不可言传”的感受，教师在描述数量关系时，也会很苍白，甚至会越讲越复杂，越讲越不易理解.在进行此类应用题教学时，以图形作为辅助，可以将抽象的关系借助图形直观地显现，便于学生理解.

例3某铁路桥长1000m，现有一列火车从桥上通过，测得该火车从开始上桥到完全过桥共用了1min，整列火车完全在桥上的时间共40s.求火车的速度和长度.

分析：此题中有两个问题：火车的速度和长度，虽然题中两个“共”字清晰地揭示了两个数量关系式，但对于“从开始上桥到完全过桥”和“整列火车完全在桥上”的理解，有不小的难度.

师：题中有哪些数量关系？

生：火车从开始上桥到完全过桥共用了1min，整列火车完全在桥上的时间共40s.可不知道如何列出数量关系式.

师：行程问题的中基本数量关系是什么？

生：路程＝速度×时间.

师：这对列出以上数量关系有什么提示？

生：路程1＝火车速度×1min；路程2＝火车速度×40s.好像不太好描述.

师：这里我们可以利用线段图来帮助我们理解以上两段描述的意思.

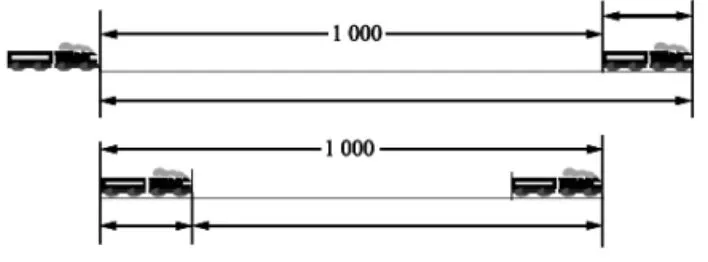
借助线段图不难看出，火车用1分钟（即60秒）的时间，行驶的路程实际上就是桥长与火车长之和；用40秒时间行驶的路程实际上就是桥长与火车长之差.

生：也就是说，桥长＋车长＝车速×60，桥长－车长＝车速×40，明白了.

……

这里采取的是线段图策略.线段图是小学解决行程问题中常用的策略之一，在行程类应用题中作用显著，到了中学阶段的学习后，学生更倾向于文字理解，忽视了线段图的应用价值.线段图的优势，是将行程问题中的路程，用线段直观地呈现出来，将诸如相向问题和追及问题中速度、时间的复杂关系，转化成显性的线段和、差之间的关系，教师需要引导学生回归问题的本质，才能让数学思维更自然地获得发展.

例4某商场五月份的销售额为300万元，六月份的销售额下降了10%，商场从七月份开始，改变了营销策略，销售额稳步上升，八月份的销售额达到了326.7万元.求七、八月份的平均增长率.

分析：这题中的增长率问题虽是平均增长率，但与平时训练的又有所不同.涉及到三个月份的增长，其中六月份还是负增长，学生对这里的增长率关系的理解还是有一定困难的，可以借助框架图，来对题中数量间进行抽象概括，直观地显现各月份之间的关系.

师：题中描述了几个月份的销售额情况？如何增长的？

生：六、七、八三个月份，其中六月份下降了10%，七、八月份都增长了，并且七、八月份增长率相同.

师：这三个月销售额分别是在哪个月的基础增长的？基础销售额都知道吗？

生：六月在五月基础上，七月在六月基础上，八月在七月基础上增长的；五月的销售额是300万元，六、七月份销售额都不知道；八月份最终销售额是326.7万元.

师：那八月份的销售额326.7万元是如何计算出来的呢？

生：可以设七、八月份平均增长率为x，但缺少六月份的销售额.

师：我们可能通过完成以下框架图来解决六月份销售额的问题.

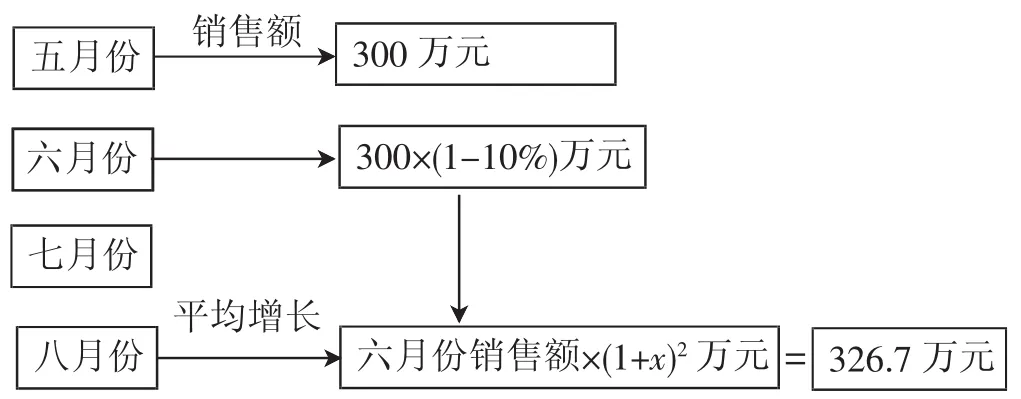
生：知道如何求解了.

……

框架图是围绕某一主题，用知识结构和框架的形式揭示数量间的关系，运用框架图对复杂的数量关系进行归类、分析、加工，有利于学生探寻问题的本质，从而实现抽象关系的显性化，实现解题的目标.

用方程（组）解决应用题的策略还有很多，本文只例谈了初中阶段最常用的三种方法.在教学时应注意的是，不要刻意要求学生固定地选择其中的某一种，而是要根据题目的特点，灵活地选用一种或综合几种，通过这些策略，让学生体会到把数学思维显性化的方法，真正提高分析问题和解决问题的能力，变“闻题色变”为“破题欢颜”，从而将感受“数学之用”提升到感悟“数学之美”.

参考文献：

1.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.王燕燕.初中数学思维显性化的思考［J］.中学生数理化（教与学），2014（6）.

3.付志芳.初中数学应用题的教学策略及解题技巧［J］.西部素质教育，2016（6）.H