把握问题本质，提炼基本方法——以具有“边边角”相等结构特征的三角形问题的探究为例

☉北京教育学院朝阳分院 白雪峰

大道至简，以简驭繁，是大智慧，更是高境界．中学数学解题教学也需要提高这样的实践智慧，追求这样的教育境界．在数学解题教学中，教师要善于引导学生把握问题本质，抓住解题关键，指导学生学会运用数学的眼光来发现和提出问题，数学的思维来分析和解决问题，数学的语言表述和阐释问题，促进学生在归纳概括解题思维过程和总结提炼解题基本方法的学习中，落实“四基”提高“四能”，发展数学核心素养．［1］

一、问题简述

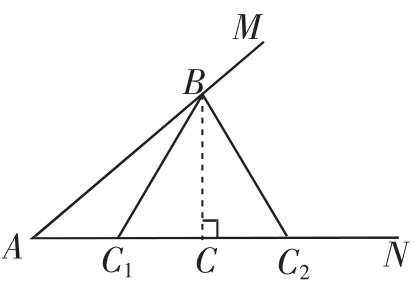
图1

如图1，∠MAN为锐角，点B在边AM上，作BC⊥AN于点C．以点B为圆心，大于BC而小于AB的长为半径作弧，交AN于点C1，C2．

在△ABC1和△ABC2中，BC1＝BC2，BA＝BA，∠BAC1＝∠BAC2，所以△ABC1和△ABC2构成了具有“边边角”相等这一结构特征的三角形．然而，这两个三角形并不全等．

但是，如果深入探究这类具有“边边角”相等结构特征的三角形，我们可以获得解决这类问题的基本方法，进而利用这种解题的基本方法解决一类问题．

事实上，我们可以通过三条途径来处理这类具有“边边角”相等的结构特征三角形问题，即可以小△ABC1“放大”为大△ABC2，或大△ABC2“缩小”为小△ABC1，或作垂线段BC构成直角三角形ACB等途径构成全等三角形，进而解决这类问题．下面举例说明．

二、方法示例

例1已知：如图2，在△ABC中，AB＝AC，点E在AB上，点F在AC的延长线上，且BE＝CF．连接EF交BC于点D．

求证：ED＝DF．

分析：在△BED和△FCD中，BE＝CF，∠EDB＝∠FDC，若证得ED＝DF，则△BED和△FCD就构成了具有“边边角”相等这一结构特征的两个三角形，但这两个三角形并不全等．由图2可知，明显有三种证法来证明ED＝DF，下面笔者选择其中的“缩小法”给出证明，即利用已知条件在大三角形里构造一个与小三角形全等的三角形．

证明：如图2，以点E为圆心，EB为半径作弧，交BE于B1，连接EB1．则有EB1＝EB＝

说明：（1）如图3，以点F为圆心，FC为半径作弧，交BC的延长线于点C1，连接FC1，则△EDB≌△FDC1，所以ED＝DF．这里利用的是“放大法”，即利用已知条件构造一个与大三角形全等的三角形．

（2）如图4，过点E作EG⊥BC于点G，过点F作FH⊥BC的延长线于点H，则Rt△EGD≌Rt△FHD，所以ED＝DF．这里利用的是“作垂线段法”，即利用已知条件通过作垂线段来构造两个全等的直角三角形．

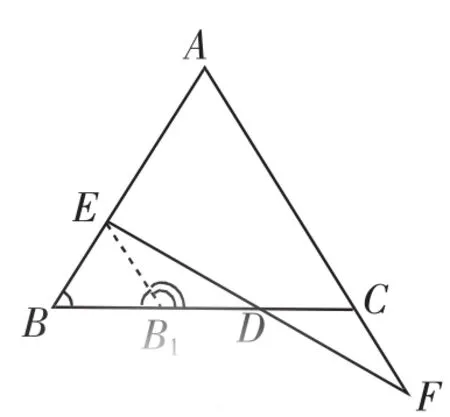
图2

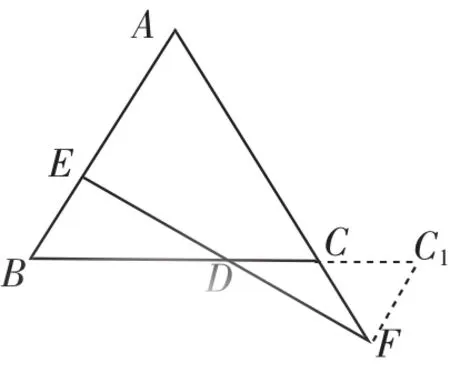
图3

图4

除以上三种证法之外，还有其他多种证法，但上述三种证法是最基本和最简单的证法．

例2已知：如图5，在△ABC（AB＜AC）中，AD为∠BAC的平分线，M为BC的中点，过点M作AD的平行线，交AC于点E，交BA的延长线上于点F．

求证：BF＝CE．

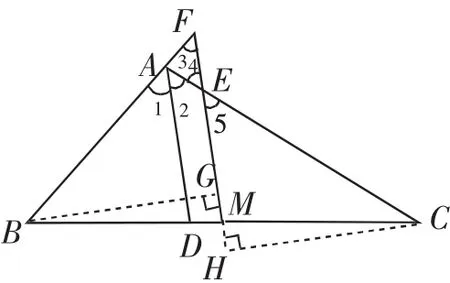
图5

分析：因为M为BC的中点，所以BM＝CM，欲证BF＝CE.因为AD为∠BAC的平分线，所以∠1＝∠2.又ME//AD，∠1＝∠3，∠2＝∠4，所以∠3＝∠4，注意到∠4＝∠5，从而∠3＝∠5，所以△MBF和△MCE构成了两个“边边角”型的三角形．

证明：如图5，过点B作BG⊥FM于点G，过点C作CH⊥EM的延长线于点H.

因为BM＝CM，∠BMG＝∠CMH，

所以Rt△BGM≌△RtCHM，

所以BG＝CH．

在Rt△BGF和△RtCHE中，

因为BG＝CH，∠3＝∠5，

所以Rt△BGF≌△RtCHE．

所以BF＝CE．

说明：用“放大”或“缩小”法也可以证明此题，请感兴趣的读者自己完成．

例3已知：如图6，在△ABC（AB＜AC）中，点E在AC上，且AB＝CE，点F、M分别为AE和BC的中点，AD为∠BAC的平分线．求证：FM//AD．

分析：欲证FM//AD，过点E作EN//AD，交BC于点N，只需要证明FM为梯形ADNE的中位线，由于F为AE的中点，所以只需要证明M为DN的中点．由于M为BC的中点，只需要证明BD＝CN，注意到AB＝CE，∠1＝∠3，所以△DBA和△NCE构成“边边角”型的两个三角形．

证明：如图6，过点E作EN//AD，交BC于点N，则有∠1＝∠3，所以四边形ADNE为梯形．

以点B为圆心，BD为半径作弧交AD于点G，连接BG，则有BD＝BG．所以∠BDG＝∠BGD，∠BGA＝∠ADC.

又∠ENC＝∠ADC，所以∠BGA＝∠CNE．

又AB＝CE，所以△BGA≌△CNE，

所以BG＝CN．

所以BD＝CN．

又BM＝MC，

所以DM＝MN，即M为DN中点．

注意到F为AE的中点，

所以FM为梯形ADNE的中位线，

所以FM//AD．

说明：请感兴趣的读者用“放大法”或“作垂线段法”来证明此题．

图6

例4已知：如图7，线段AB交圆O于C、D两点（AB不过圆心O），且AC＝BD，作AF切圆O于点F，作BE切圆O于点E，AF、BE在线段AB的异侧，连接EF交线段AB于点M．

求证：CM＝MD．

证明：如图7，分别延长FA、BE交于点G．

因为AF和BE为圆O的切线，

所以GE＝GF，即△GEF为等腰三角形．

所以AF2＝AC·AD，BE2＝BD·BC．

因为AC＝BD，

所以AD＝BC．

所以AF2＝BE2，即AF＝BE．

图6中的直线型与例1相同，

所以AM＝MB，CM＝MD．

说明：如果不应用图1的结论，可以应用三角形全等证明此题，这也是比较简单的方法．

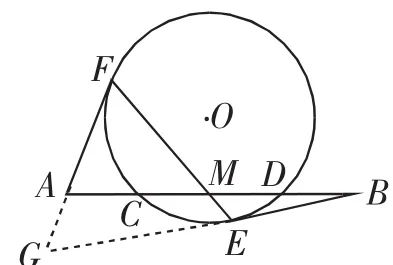
图7

三、写在后面

纵观问题提出和方法示例，笔者提出了一类具有“边边角”相等这一结构特征的三角形问题，基于典型例题呈现了“放大”“缩小”和“作垂线段”三种问题转化的基本方法，其目的都是要构成全等三角形．在深入分析的基础上，应用全等三角形的相关知识给出这类问题完整的证明过程，展示了问题探究和方法提炼的全过程．

实际上，平面几何历来是培养学生推理能力和理性精神的上佳载体，通过类似教与学过程的设计与实施，不仅可以促进学生夯实基础知识，强化基本技能，还可以领悟基本的数学思想．进一步地，通过深刻反思上述数学问题的发现、提出、分析和解决的探究过程，助力学生获得深度参与数学探究活动的基本经验．［1］

因此，作为数学教师，要善于引领学生深入挖掘几何问题内在的数学本质特征，引导学生学会运用数学的眼光、数学的思维和数学的语言，持之以恒地充分发掘几何问题中蕴含的思维力量，将数学之大道自然融入“四能”培养的全过程之中，把学生获得解题能力的眼前利益和发展数学核心素养的长期利益有机融合起来，切实发挥平面几何的教育价值和育人功能．［2］

参考文献：

1.中华人民共和国教育部．普通高中数学课程标准（2017年版）［S］．北京：人民教育出版社，2018年1月.

2.白雪峰．一道中考数学模拟试题的证明与拓展，中国数学教育，2015（5）.H