解信赖域子问题的改进的平均欧拉切线法

贾新辉，王希云

(太原科技大学应用科学学院，太原030024)

其中，gk=!f(xk)，Bk∈Rn×n是目标函数在当前迭代点x(k)的海塞矩阵!2f(xk)的近似，Δk是信赖域半径，s∈Rn是待求变量.Δk取不同的值时，信赖域子问题(1)的解s*构成了空间最优曲线［1］。

对于海塞矩阵正定的情形，运用折线法求解子问题(1)较为普遍.常用的折线法有单折线法［2］、双折线法［3］、切线单折线法［4］、混合折线法［5-6］、不定折线法［7-8］、双割线折线法［9］等.2014 年王希云、李亮根据信赖域子问题解的最优曲线的参数方程建立了微分方程模型［10］，并针对该模型提出一

讨论如下二次模型的信赖域子问题的求解:种求解子问题(1)的平均欧拉切线算法［11］。

平均欧拉切线算法的思想是在微分方程模型［10］的基础上，采用梯形公式［12］构造一条折线，来近似代替最优曲线求解子问题.数值结果表明该算法比切线单折线法更有效，但缺点是步长形式复杂，计算时间相对较长，且文［11］中定理5.1的条件可进一步改善。

文［11］运用定理5.1的假设条件可证明构造的折线满足引理 6.4.1［13］，但前提又要利用引理5.1的结论2［11］.为了证明该结论，构造了较为繁琐的步长，导致迭代次数多，计算时间较长.本文为简化步长形式，将文［11］的假设条件修正为:

并在该条件下证明了算法的适定性，也不需利用结论2［11］.且步长可简化为:

其中n=0，1，2，…，ω为限制每次迭代所能达到的最大步长值.从而提出了求解子问题(1)的改进的平均欧拉切线法.文章最后将本文算法和平均欧拉切线法进行了比较，数值实验表明新算法较平均欧拉切线法具有迭代次数少、运算时间短等优点。

1 改进的平均欧拉切线路径的性质分析

求解微分方程的梯形公式为:

改进的平均欧拉切线记为:

其中 φ0=0，φi+1= φi+hi，i=0，1，2，3，…，N－1.

定理2.1 若B 对称正定，则当n=0，1，2，…，N－1时，满足:

证明:当 n=0，1，2，…，N － 1 时，有:

由(3)得:

定理2.2 若 B 对称正定，当 n=0，1，2，…，N－1时(4)式成立.则s(τ)满足:

(1)‖s(τ)‖2关于τ为连续单调递减函数;

(2)qks(τ[])关于τ为连续单调递增函数.

由(4)式得:

故对 τ∈［φi，φi+1］，i=0，1，2，3，…，N － 1时，‖s(τ)‖2关于τ为单调递减函数.

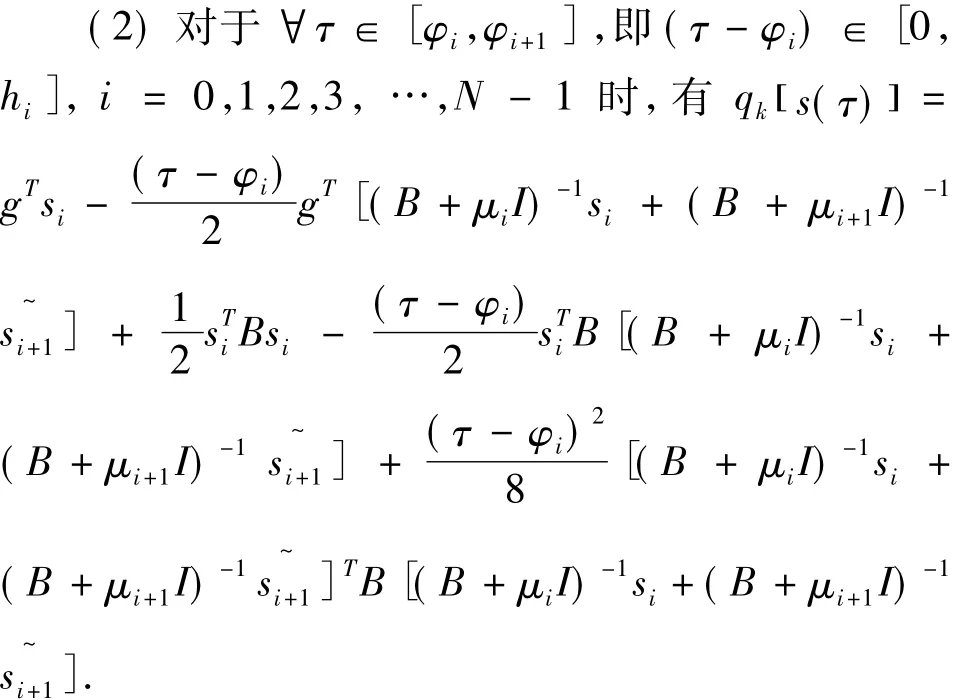
求导得:

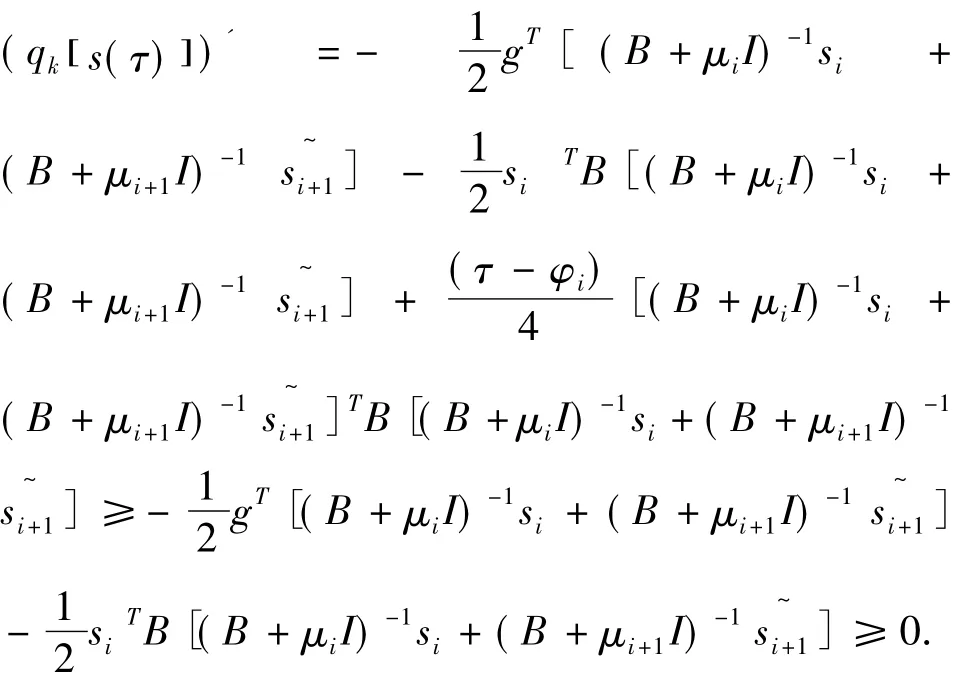
故对 τ∈［φi，φi+1］，i=0，1，2，3，…，N － 1时，qks(τ[])关于τ为单调递增函数.证毕。

2 算法过程

下面给出本文算法的具体步骤:

Step 1给出梯度 g，正定矩阵 B，信赖域半径Δ.

Step 2计算牛顿步s0=－B－1g.

Step 3若‖s0‖2≤ Δ，则取s*=s0，算法终止.否则，转Step 4.

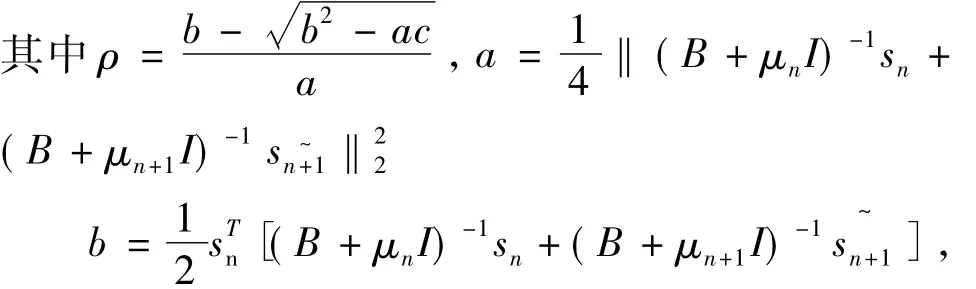
c= ‖sn‖22－ Δ2，算法终止.否则，令n:=n+1，转 Step 5.

3 数值实验

对于信赖域子问题(1)，本文采用给定的测试函数1和测试函数2，针对不同的信赖域半径Δ，选取限制步长ω=2，运用MATLAB将本文中改进的平均欧拉切线算法进行数值实验.并与文［11］中提出的平均欧拉切线法进行数值结果的比较，结果分别列在如下四个表格中.

表1 Function 1最优解的数值结果Tab.1 The numerical results of the optimal solution of Function 1

表2 Function1的运行时间及迭代次数结果Tab.2 The running time and number of iterations of Function 1

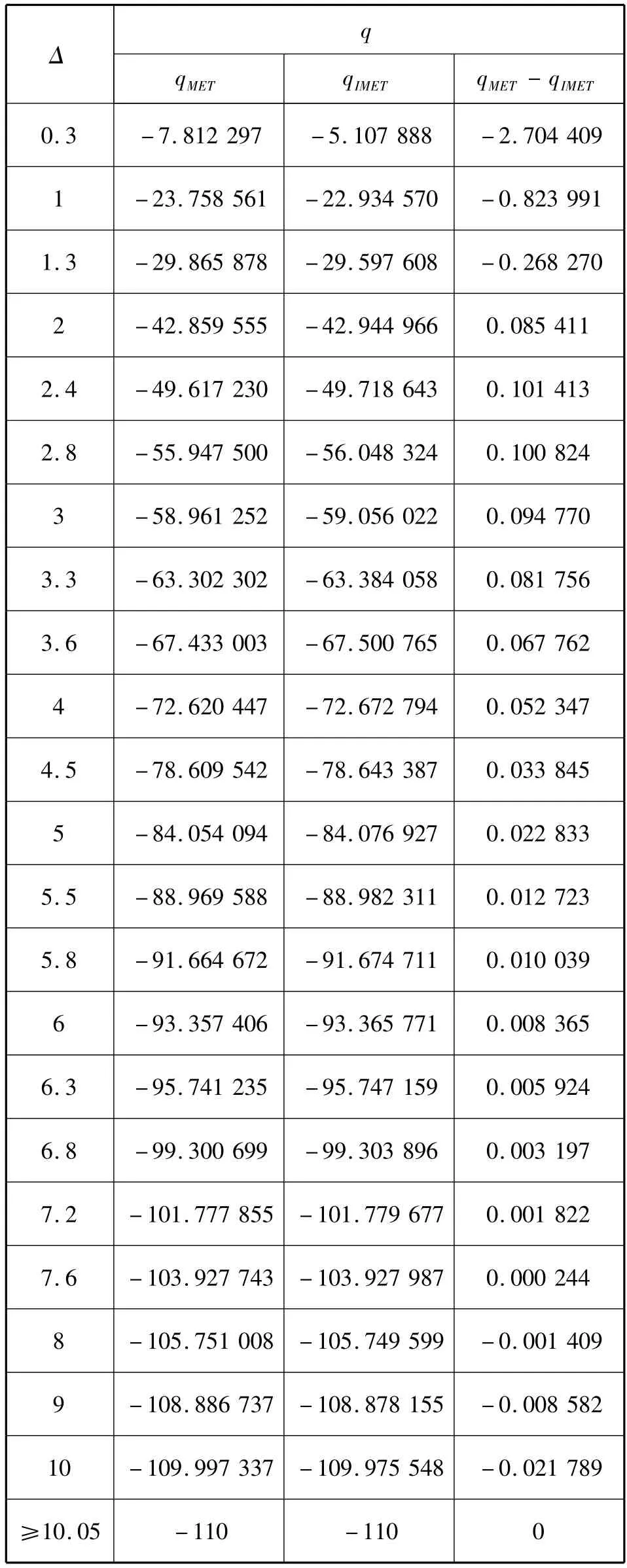
表3 Function 2最优解的数值结果Tab.3 The numerical results of the optimal solution of Function 2

表4 Function 2的运行时间及迭代次数结果Tab.4 The running time and number of iterations of Function 2

表1中，Δ表示信赖域半径，q表示最优解的函数值，t表示求解子问题所用的时间，n表示迭代次数，MET表示平均欧拉切线法，IMET表示改进的平均欧拉切线法，tMET表示平均欧拉切线法所用的时间，tIMET表示改进的平均欧拉切线法所用的时间，nMET表示平均欧拉切线法的迭代次数，nIMET表示改进的平均欧拉切线法的迭代次数，qMET表示平均欧拉切线法求得的最优解的函数值，qIMET表示改进的平均欧拉切线法求得的最优解的函数值，测试函数见附录。

由上述实验结果可以得出，在信赖域半径较小时，本文提出的改进的平均欧拉切线法明显要比平均欧拉切线法的计算速度高，迭代次数少，且在计算结果的精确度上与之相近.对于Function 1，当信赖域半径2.5≤Δ≤7.4时，改进的平均欧拉切线法求得的信赖域子问题(1)的最优值要比平均欧拉切线法的好，当信赖域半径1.3≤Δ≤及8≤Δ≤10时，本文算法不如平均欧拉切线法的结果好;对于Function 2，当Δ为2≤Δ≤7.6时，本文算法比平均欧拉切线法的结果好，当Δ为0.3≤Δ≤1.3及8≤Δ≤10时，平均欧拉切线法的结果较好.而当信赖域半径Δ=‖B－1g‖2时，两种方法求得的结果一样。

总体来看，本文提出的改进的平均欧拉切线法要比平均欧拉切线法的计算效率高，迭代次数少，该算法可以很好地近似最优曲线，是有效可行的。对 于 Function 1，‖B－1g‖2= 10.308.对 于Function 2，‖B－1g‖2=10.05 .

附录:测试函数

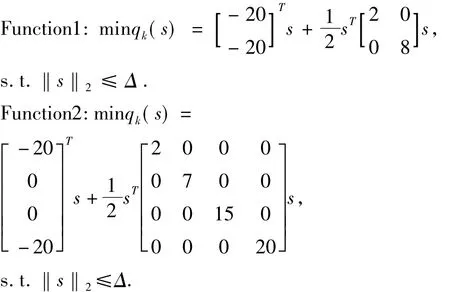
参考文献:

［1］ 徐成贤，陈志平，李乃成.近代优化方法［M］.北京:科学出版社，2002.

［2］ POWELL M J D.A Hybrid Method for Nonlinear Equations［C］.//Numerical Methods for Nolinear Algebraic Equ-ations，Rabinowtiz P.ed.London:Gordon and Breach，1970.

［3］ DENNIS J E，MEI H H W.Two New Unconstrained Optimization Algorithms Which Use Function and Gradient Values［J］.Journal of Optimization Theory and Applications，1979，28(4):453-482.

［4］ 赵英良，徐成贤.解信赖域子问题的切线单折线法［J］.数值计算与计算机应用，2000，21(1):77-80.

［5］ 张立，唐志强.解信赖域子问题的混合折线法［J］.南京师范大学学报:自然科学版，2001，24(1):28-32.

［6］ 赵丹.解信赖域子问题的混合折线法［J］.徐州师范大学学报:自然科学版，2009，27(3):38-41.

［7］ CHEN J，SUN W Y.Nonmonotone Adaptive Trust Region Algorithms With Indefinite Dogleg Path for Unconstrained Minimization［J］.Northeast Math Journal，2008，24(1):19-30.

［8］ ZHANG J Z，XU C X.A Class of Indefinite Dogleg Path Methods for Unconstrained Minimization［J］.SIAM Journal on Optimization，1999，9(3):646-667.

［9］ 王希云，邵安.一种双割线折线法求解信赖域子问题［J］.应用数学，2012，25(2):419-424.

［10］ 李亮，王希云，张雅琦，等.一种求解二次模型信赖域子问题的休恩算法［J］.太原科技大学学报，2014，35(2):151-155.

［11］ 李亮.一类求解信赖域子问题的欧拉算法［D］.太原:太原科技大学，2014.

［12］ 颜庆津.数值分析［M］.北京:北京航空航天大学出版社，2006.

［13］ 李董辉，童小娇，万中.数值最优化算法与理论［M］.北京:科学出版社，2010.