四旋翼飞行器串级PID控制设计与实现

靳亚磊，李 虹，李昕涛

(太原科技大学电子信息工程学院，太原030024)

四旋翼飞行器是一种结构简单、易于操作，应用价值很高的微型飞行器。由于它还具备一定的负载能力和特殊的悬停功能，被广泛应用于军事侦查，民事航拍等方面［1］。由于它欠驱动、强耦合、非线性的特点，使得实际应用中控制器的设计难度很大。虽然近年来出现了很多智能控制算法，可以达到精确的控制效果，但需要较高的运算速度及时响应，现有的微处理器很难做到这一点，所以目前主流控制仍是PID控制算法。

文献［2］中硬件采用ARM Cortex-M3为内核的STM32F1系列芯片作为处理器，程序设计采用的是中断方式进行执行任务。硬件缺少扩展功能且程序缺乏系统性。文献［3］只运用了PD控制算法进行姿态控制，且使用两个单片机进行控制，造成硬件资源浪费。文献［4］使用分散PIDNN算法进行姿态控制，并采用ATMEGA系列单片机作为处理器，虽然有一定的控制效果，但是控制器的实现较复杂。本文结合已有的PID控制器，采用双闭环结构，进行串级PID控制设计，以四元数互补滤波方法进行实时姿态解算，以高性能的STM32F4系列芯片作为处理器，以时间片轮方式进行任务循环执行，最后通过电子调速器控制电机转速，达到实现姿态和高度控制的目的。

1 四旋翼飞行器飞行原理

四旋翼飞行器一般分为两种结构，“十字”和“X”型结构。本文以“X”型为例，如图1所示，机架呈对称结构，M1，M2，M3，M4为四个电机，分别安装在机架顶端，且相邻电机的转速相反，以此抵消旋翼转动时内部产生的陀螺效应，F1，F2，F3，F4是旋翼旋转产生向上的升力，通过改变四个电机的转速，可以实现飞行器如下多种飞行模式。

垂直运动与悬停:四个电机同速旋转时，向上的升力之和大于重力时，就会向上飞行，到达一定高度后，减小转速到升力之和等于重力时，便可保持悬停状态。若再减小转速则下降飞行。

滚转运动与左右飞行:飞行器处于悬停状态下，同时增加或减小M1，M4转速，则飞行器就会绕图中x轴转动而倾斜一定的角度，进行滚转运动或左右飞行。

俯仰运动与前后飞行:悬停状态下，同时增加或减小M1，M2转速，则飞行器就会绕图中y轴转动而倾斜一定的角度，进行俯仰运动或前后飞行。

偏航运动:悬停状态下，同时增加或减小四个电机中任意对角线上的两个电机转速，则飞行器就会绕图中z轴转动，进行顺时针或逆时针转动航向。

图1 四旋翼飞行器简化结构图Fig.1 Simplified structure of four-rotor aircraft

2 四旋翼飞行器硬件组成

四旋翼飞行器硬件组成可分为:测量模块、控制模块、执行模块、无线传输模块，显示单元等组成。如图2所示。

控制模块:采用ARM Cortex-M4内核的STM32F407VGT6芯片作为主控制芯片，具有168 MHz和1 M Flash，拥有强大的计算处理能力，并且可提供丰富的扩展接口，可同时接多种外部传感器设备。

测量模块:主要进行飞行器姿态和高度的测量，采集后的数据给主控制单元进行滤波处理和姿态解算。由于飞行器空中飞行环境复杂多变，单个传感器测量误差大，不能保精确测量。本文采用多种传感器测量，多种数据融合处理，如MPU-6050和AK8975磁力计组合成的9轴运动处理传感器、MS5611气压计。它们通过I2C总线接口与微处理器进行通信;US-100超声波模块和GPS测量单元以USART接口与微处理器进行通信。用四元数互补滤波方法进行数据整合处理［5］，最后得出较为准确的姿态角度。

无线传输模块:控制指令的发送和飞行数据的传输都需要以无线的方式传送。本文通过遥控器对飞行器进行指令发送，并以蓝牙模块BT06或无线数传模块通过USART接口把飞行器的飞行数据传输给手机或电脑端，进行监控显示，同时也可以在显示端对传感器进行校准和参数调节。

执行模块:由电子调速器和直流无刷电机、螺旋桨组成。

飞行器的整体供电为锂电池，分别给四个电机供电，通过电子调速器给控制单元供电。其它单元由控制模块进行供电。系统框图如图2所示。

图2 四旋翼飞行器飞行控制系统框图Fig.2 Block diagram of flight control system for four-rotor aircraft

3 姿态数据解算与控制器的设计

3.1 姿态数据解算与高度测量

3.1.1 姿态角度解算

姿态角度解算是飞行控制中姿态信息处理的主要部分。若使用单传感器测量，存在较大的测量误差和外界环境干扰影响。本文用多种传感器进行姿态数据测量，以四元数互补滤波算法进行姿态数据融合处理，得出较为精确的姿态角度。

在常见的姿态表示方法中，欧拉角表示的物理意义明确，但是存在奇点，即在角度为90°时，存在大量的超越函数运算;方向余弦虽然无奇异点，但是存在六个冗余参数，计算量大［5-6］。所以本文用四元数法进行姿态表示，不但没有奇异点存在而且计算快速精确。

多个传感器工作时，陀螺仪测量姿态角度是通过角速度进行积分求得，长时间会出现积累误差，所以要通过加速度计和磁力计进行误差校准。

式中:ψcor为磁力计的校正因子，ψMag和ψ分别是AK8975测量后标定的航向角和四元数更新解算出的航向角。gx(t+1)和gx(t)分别为陀螺仪当前刻测量值和上一时刻测量值，Th为积分时间常数，kp，ki为相应系数。其中，

式中:q0，q1，q2，q3为四元数元素，其中 q0为实数，初值为 1，其它为虚数，初值为0.Vx，Vy，Vz为机体坐标系下加速度在三个轴上的重力分量，以四元数形式的表示。ax，ay，az为加速度计测量处理后的值;ex，ey，ez为校正误差。校正之后运用一阶龙格库塔法进行四元数姿态数据更新［7］。

式中:Q(t+1)和Q(t)分别为四元数当前时刻和上一时刻的值。更新后的四元数进行欧拉角转换［8］，解出姿态角。

3.1.2 高度测量

高度测量一般分为两种模式，一种是超声波定高，一种是气压计定高模式。本文用的是US-100超声波模块，超声波测量距离有限，可实现2 cm～4.5 m的非接触测距功能，拥有2.4～5.5 V的宽电压输入范围，静态功耗低于2 mA，自带温度传感器对测距结果进行校正。

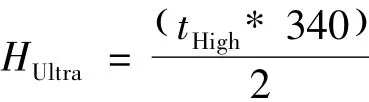
式中:HUltra和tHigh分别为测量距离和高电平持续时间，因为已经进行温度校正，声速为340 m/s.

本文所用的MS5611是由压阻传感器和传感器接口组成的新一代高分辨率气压计，分辨率可达到10 cm.功能是把测得未补偿的气压值经ADC转换成24位的数字值D1，同时也可以输出一个24位的数字温度值D2.以I2C总线与主控板通信并经过以下处理得出温度和高度值。温度计算如下。

式中:dT是实际和参考温度之间的差异，参考温度C5=33 464，温度系数的温度C6=28 312，Tt为测量温度。

温度的变化需要二阶温度补偿，如图3所示。计算温度补偿下的气压值与高度

式中:OFF为实际温度抵消，SENS是实际温度灵敏度，压力灵敏度C1=40127，压力抵消C2=36924，温度压力灵敏度系数C3=23317，温度系数的压力抵消C4=23282.C1－C6为16位无符号整型数据类型［10］。

图3 二阶温度补偿流程图Fig.3 Second － order temperature compensation flow chart

3.2 串级PID控制器设计

3.2.1 姿态控制器设计

四旋翼飞行器的姿态控制在整个控制系统中是最重要的同时也是最难的环节。因为在空中飞行中存在各种不确定的干扰，单环PID只有角度控制，很难保证飞行器在复杂环境中的稳定性，为了提高飞行器抗干扰能力，增加了内环角速度PID控制。

图4 姿态角串级PID控制流程框图Fig.4 Attitude angle cascade PID control flow block diagram

从图4中可以看出，内环姿态角速度由陀螺仪进行测量，外环角度由姿态解算求出欧拉角，在程序设计中数字式PID控制表达式如下

式(10)中eA和式(11)中ea分别是角度误差和角速度误差，为了防止控制变量突变内环角速度控制引入α (0＜α＜1)作为权重，e=为误weight差权重，W 为取 150.Kp，Ki，Kd 为控制器参数，T 为姿态测量更新时间周期。

3.2.2 高度串级PID控制器设计

图5 高度串级PID控制流程框图Fig.5 Altitude cascaded PID control flow block diagram

从图5可以看出，内环高度速度通过加速度测量值和高度测量值整合而得。先从加速度计中提取垂直方向的分量，积分成相应的速度值wzspeed0，再与测量出的速度值hspeed作如下处理。

式(13)中eH和式(14)中es为高度误差和高度速度误差，Hexp为期望高度速度，即为外环高度控制器输出，Kp，Ki，Kd为控制器的数，T为高度测量更新周期。PIDAltitude和PIDspeed为高度和高度速度控制器输出。

得出控制量之后，由于四旋翼飞行器飞行模式为“X”结构，要对控制量进行整合，作为电机m1，m2，m3，m4 的输入量。PIDalt，PIDroll，PIDpitch，PIDyaw分别为高度串级 PID 输出，姿态角串级PID输出。

4 仿真实验结果与分析

为实现姿态稳定控制，先进行MATLAB仿真［9］，仿真实验参数:m=0.523 kg，g=9.8 m/s2，l=0.245 m，

Ix=Iy=0.062 kg·m2.其中l为旋翼中心到飞行器中心的距离，b，d分别为推力系数和阻力系数，Ix，Iy，Iz为转动惯量。仿真实验加入有界的干扰为|2|，姿态角度初值为［10，10，0］，最后稳定为［0，0，45°］.为便于分析仿真结果，以下性能指标来分析仿真实验数结果:稳定时间为ts，超调量为Mp，跟踪误差为σ.

仿真实验结果如图6所示。

由图6可以看出，同等情况下，在ts=0.5 s左右，串级PID控制的姿态角便可达到期望角度，超调量Mp几乎为0;单级PID控制则在ts=2 s时才稳定，且稳定过程中出现大的超调，Mp=25%.由于仿真实验中加入了外界干扰，稳定后从小图可以看出串级PID控制的跟踪误差几乎为0，而单级PID控制时σ= 0.3，且只能在期望值附近抖动。仿真实验结果表明所设计的控制器具有较好的控制效果［10］。

图6 姿态角和高度仿真对比实验图Fig.6 Comparison of attitude angle and altitude simulation

控制器参数如表1所示:

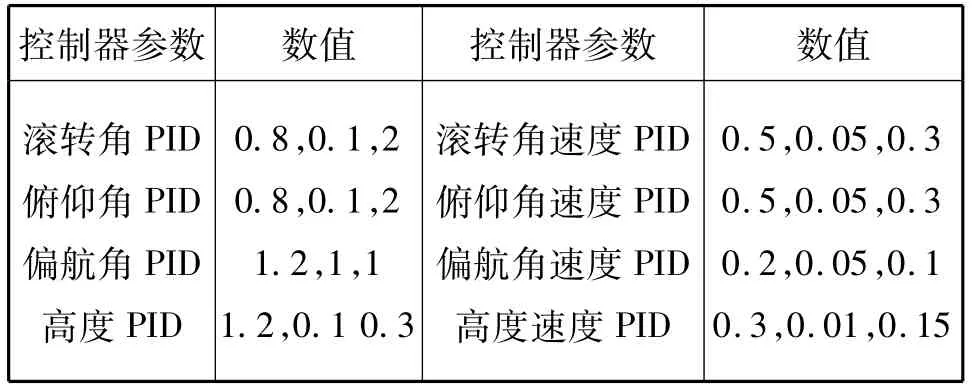
表1 控制器参数Tab.1 Controller parameter

而后把仿真实验中的控制器参数写入程序中，飞行稳定后互补滤波算法姿态角测量波形如图7所示。

由图7可以看出，室外飞行实验中，飞行器在悬停时测量角度基本水平，滚转角和俯仰角测量误差在±1.5°范围内，航向角控制误差在 ±2.5°范围内。

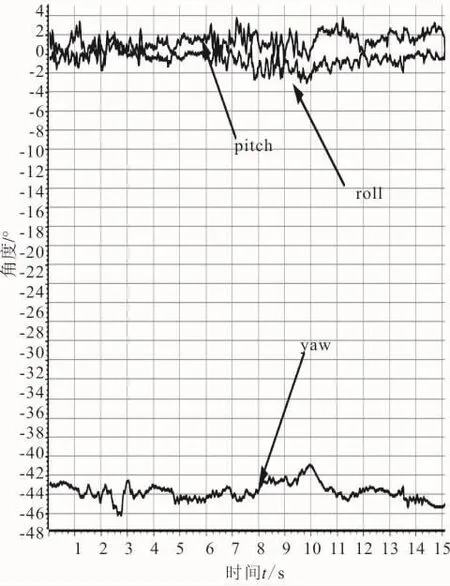
图7 姿态角度测量值Fig.7 Attitude angle measurement

图8 室外空中飞行Fig.8 Outdoor air flight

图8 中可以看出，飞行器在室外能够实现稳定飞行及悬停，有较好的飞行控制效果。

5 总结

四旋翼飞行器姿态控制是飞行控制的核心控制，本文针对此核心控制进行了串级PID控制研究。在室外飞行中有外界干扰下为了得到精确的姿态角，使用了多种传感器进行测量，采用四元数互补滤波算法进行姿态解算。采用串级PID姿态和高度控制，与单级PID控制相比，增加了内环角速度和高度速度控制，提高了飞行器的抗干扰能力，增强了系统的鲁棒性。

参考文献:

［1］ SALIH AL，MOGHAWEMI M，MOBAMED HAF，et al.Modelling and PID controller design for a quadrotor unmanned air vehicle［C］//IEEE International Conference on Automation Quality and Testing Robotics.IEEE，2010:1-5.

［2］ 贾峰，孙曼，秦磊.基于STM32的四旋翼飞行姿态串级控制［J］.科学技术与工程，2015，15(6):220-225.

［3］ 侯永锋，陆连山，高尚德，等.基于PD算法的四旋翼飞行器控制系统研究［J］.机械科学与技术，2012，31(3):359-362.

［4］ 李秀英，刘彦博.基于PWM的四旋翼飞行器控制方法［J］.吉林大学学报信息科学版，2011，29(5):464-472.

［5］ 丁君，赵忠华.AHRS航姿解算中的两种滤波方法的比较研究［J］.计算机仿真，2013，30(9):60-65.

［6］ 乔相伟.基于四元数非线性滤波的飞行器姿态确定算法研究［D］.哈尔滨:哈尔滨工程大学，2011.

［7］ 秦永元.惯性导航［M］.北京:科学出版社，2014.

［8］ 朱文杰，王广龙，高凤岐，等.基于MIMU和磁强计的在线实时定姿方法［J］.传感技术学报，2013，26(4):536-540.

［9］ 肖勇，孙志毅.四旋翼飞行器极点配置姿态控制器设计［J］.太原科技大学学报，2016，37(5):354-358.

［10］ 李天涯.四旋翼飞行器姿态控制及轨迹规划的研究［D］.北京:北京理工大学，2016