联合去马赛克和去噪

任 娟

(太原科技大学应用科学学院，太原030024)

彩色图像通常是通过数码相机由滤色器阵列(CFA)所覆盖的单一传感器获得的.为了重建一个全彩色图像，需要从传感器所传递的原始数据进行插值运算，这种恢复丢失的颜色信息的过程叫做去马赛克.在由传感器获取图片的过程中，由于光子计数和电热效应的影响往往会引入噪声所以不得不考虑去噪问题.去噪和去马赛克作为彩色图像处理的两个过程，先处理哪个都会带来不足之处，详细可以参考文献［1］.联合去噪和去马赛克不失为一种行之有效的好方法，这种方法在文献［2］中提出来。随后各种处理技术相继涌现，比如运用小波处理［3］，Condat将在频域去马赛克［4］的方法延伸到联合去噪和去马赛克［5］。2012年，Condat使用基于有界变差的正则化模型重建图像［6］，并用原始对偶算法求解，取得了很大的进步.利用全变差作为正则化项在图像处理中也是常用的方法，为了更好地重建图像，各种形式的全变分模型［7－8］被提出。

目前，Rudin等人［9］已经对图像处理问题的TV正则化模型做了介绍，由于基于有界变差的正则化项是不可微的，有效求解TV最小化长期以来一直有挑战性，但在大规模凸非光滑优化不断进展的情况下TV最小化变得相对容易求解了，如原始对偶分裂方法和交替方向乘子法等。全变分能够很好的保持边缘，但会将连续光滑的信号变为分段的等值信号，从而导致“阶梯效应”。本文试图建立新的正则化项削弱这种现象。

本文安排如下:第二部分对所建的模型进行描述，第三部分是实验和相应的结果，最后得出结论。

1 模型的描述

1.1 对离散TV定义的回顾及分析

设函数 s(t1，t2)∈R2，梯度为马丕s(t1，t2)=，s的全变分定义为梯度的L1范数，即 TV(s)= ∫R2马丕s(t1，t2) dt1dt2，其中该TV有旋转不变的优质特征:即在平面内旋转s该TV值不变。

一幅大小为N1×N2的离散灰度图像x定义在Ω ={(1，2，…，N1) × (1，2，…，N2)}上，位置(k1，k2)的像素值为x［k1，k2］.利用离散的像素值并且保持连续TV的数学特性来定义离散TV是有难度的。所谓的各向异性全变分定义如下:

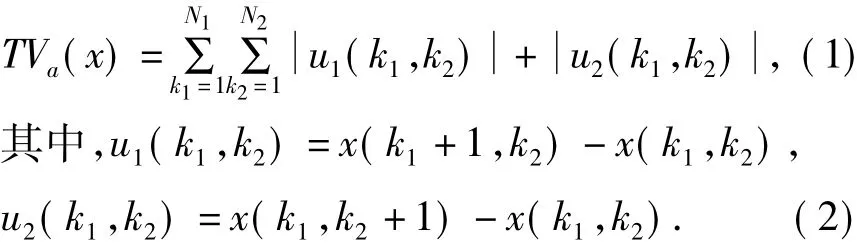
图像的最后一行和最后一列有界变差定义为0.各向异性很少用来定义离散TV，它不适用于倾斜结构，这种情况下会使TV值比实际值大，比较适用于水平和垂直结构［10］。所以常用的是各向同性TV，它的表达式为:

为了对不同的TV值进行比较，做了以下工作，给出各种图形如图1所示，图片大小为N×N，当N足够大时忽略边界的影响。这里考虑了各种各样的情况，图1中的(2)(3)(5)分别是图2中(a)(b)(c)的离散形式。黑色和白色分别对应0和1;在(2)中所对应的值依次为0，，1;(3)依次为 0，，1;(5)依次为0，，1，，0.图片的水平翻转用“f”表示，见图片(1)和(1f);负版本用n表示。表1给出了图1中各情形对应的不同定义的TV值，其中的绿色部分是适合该图形的方法对应的TV值。倾斜结构用各向同性有界变差合适，(1)(4)(7)用各向异性有界变差效果好。表1的最后一列为本文的正则化项，它是将各向同性有界变差同L2范数进行了结合，因为常用的是各向同性有界变差，对于非倾斜结构显然不合适，在这基础上与L2范数进行了结合，使数值和各向异性有界变差值相近，对于倾斜结构，可以调节后面一项的系数使它很小。

图1 列举表1中要计算TV值的图形Fig.1 Some patterns，for which we report the value of the TV in Tab.1

图2 图1中(2)(3)(5)的连续形式Fig.2 In(a)，(b)，(c)，continuously-defined images whose cell-average discretization yields Fig.1(2)，(3)，(5)，respectively

1.2 提出新的正则化模型

表1 图1的图形所对应的TV值Tab.1 TV Results for Fig.1

现今，稀疏表示是图像处理领域常用的方法，压缩感知是稀疏表示的一个很重要的应用，而压缩感知通常支持两个测量之间几乎没有关系的不相关系统.而事实上，很多问题是相关系统.2016年，Lou［15］导出L1－L2的邻近算子，并运用于前向后向裂算法(FBS)和交替方向乘子法(ADMM)求解，结果都优于L1范数.这些研究适用的情形是解本身具有稀疏性的情形.因此，一个非常自然的想法就是探索解在变换意义下具有稀疏性的情形，同样将两者结合的效果是否会更好.根据1.1节对各项同性和各向异性的有界变差的分析，本文尝试了在各向同性的有界变差基础上加上L2范数平方的δ倍，记为:

即L1+，看是否存在δ≠0比δ=0时的图片质量更好.上式中，D为离散梯度算子，Dx=(u1，u2)，u1，u2如式(2)式所示。

2 实验和相应的实验结果

2.1 预备知识

这部分将利用以上介绍的内容解决彩色图像联合去马赛克和去噪，我们知道三个颜色通道是有联系的，将它们转换到色度亮度通道会比较好地保持颜色信息［6］，所以下面做一个正交变换(5)，

其中，()=DxC1，()=DxC2，(，)=τ·DxL，参数τ＞0，它在调节被修复图像亮度和色度平衡起重要作用，本文取为0.2，文献［13］有详细介绍。

假设所求的图片大小为N1×N2，通过解下面凸优化式子求，

b定义在 Hilbert空间 Υ，A是 X到 Y的线性算子，

Ω是X的闭凸子集，u＞0是数据项和正则化项的调控参数，彩色图像有在亮度色度空间有一个亮度分量xL，两个色度分量xC1，xC2，在一个像素点k=(k1，k2)的信息可表示为 x［k］=［x1［k］T，x2·［k］T，x3［k］T］T，‖D*D‖≤8［12］，其中，

2.2 实验

为了证明提出的TV的有效性，做了两个实验:灰度图像去噪和超分辨率重建，彩色图像联合去马赛克和去噪.这两个应用可以描述为问题(6)，运用于灰度图像时，A为加噪和采样的过程，

彩色图像时A为加马赛克的过程。将实验结果与文献［6］作比较，文献［6］采用各向同性的有界变差作为正则项，如式(3)所示，用基于邻近算子的原始对偶不动点算法［14］解提出的TV模型，具体如下:

邻近算子的表达式为:

(I－)(x)=projε(x)，projε为从 R6n到半径ε的球l6，∞的投影算子(彩色图像)，或R2n到半径ε的球l2，∞的投影算子(灰度图像)，

将用峰值信噪比(PSNR)作为图片质量的评价标准，灰度图像的PSNR描述为:PSNR=10log10·

I0表示原始图像，I还原得到的图片.彩色图片用CPSRN来评价，CPSRN表达式和PSNR相同，其中的MSE有所变化，MSE=［k］)2/3N1×N2.

图3是实验原图，图4是各种TV运行的结果，本文参数设置为，0＜λ ＜1/8，0＜γ＜2/(1+8uδ)，将对μ和δ的取值进行对比，寻求最优值.下面四张表展示的是它们的PSNR值，对δ前面取“+”和“－”分别进行探索。

图3 原图Fig.3 Initial image

图4 运行结果Fig.4 Experiment results

表2 彩色图像的CPSNR值Tab.2 CPSNR of parot

可以看到本文的TV用于彩色图像和灰色图像所作出来的效果都优于各向同性的有界变差。

3 结论

提出一种新的正则化模型，针对传统的各向同性有界变差对水平竖直结构处理效果的缺陷而作第一张表是δ为正时的结果，第二张是为负的时候的结果，可以看到在 u=10，δ=0.01时，取值最好。

“－”表示值为负值，从表3可以看出u=1，δ=0.01时，图片的峰值信噪比达到最大，u=1，δ=0时，即各向同性有界变差，PSNR为27.33，小于两种测度之差的结果.

从表2，表3可以看出，运用两种测度之间的关系比单独使用各向同性有界变差效果要好，而且大多好的效果出现在δ前面的符号为“+”时.下面是δ=0和δ≠0中结果最好的图，即分别使用各向同性有界变差TVi和本文所提出的TVp，也就是红色部分的图。了改进，在彩色图像去马赛克和去噪方面取得很好的效果。本文只在一部分参数组合中选取较优的参数。今后将进一步研究如何根据内蕴的性质选取正则化参数，并根据彩色图像通道间的内在联系建立相应的求解模型。

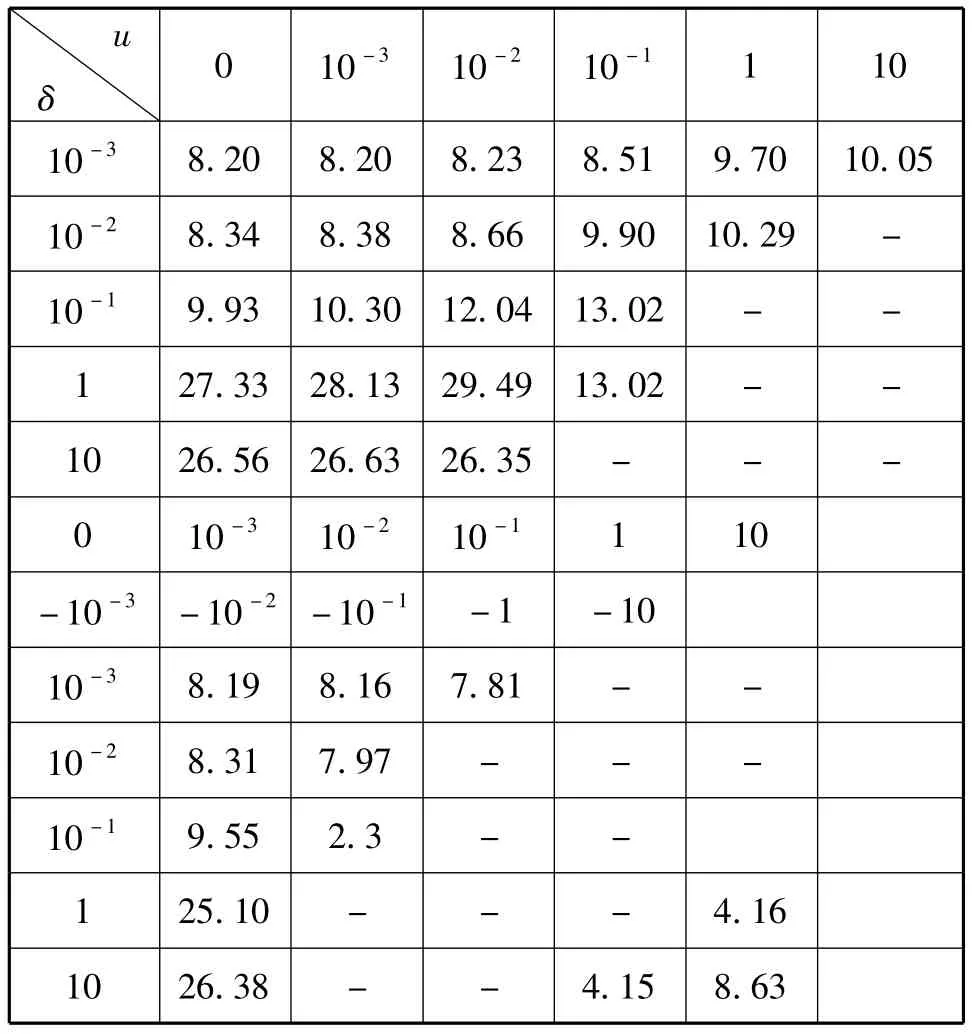
表3 灰度图像的PSNR值Tab.3 PSNR results of monarch

参考文献

［1］ MENON D，CALVAGNO G.Color image demosaicking:An overview［J］.Signal Processing:Image Communication，2011，26(8):518-533.

［2］ HIRAKAWA K，PARKS T W.Joint demosaicing and denoising［J］.IEEE Transactions on Image Processing，2006，15(8):2146-2157.

［3］ HIRAKAWA K，MENG X L.An empirical Bayes EM-wavelet unification for simultaneous denoising，interpolation，and/or demosaicing［C］//2006 International Conference on Image Processing.IEEE，2006:1453-1456.

［4］ DUBOIS E.Filter design for adaptive frequency-domain Bayer demosaicking［C］//2006 International Conference on Image Processing.IEEE，2006:2705-2708.

［5］ CONDAT L.A simple，fast and efficient approach to denoisaicking:Joint demosaicking and denoising［C］//2010 IEEE International Conference on Image Processing.IEEE，2010:905-908.

［6］ CONDAT L，MOSADDEGH S.Joint demosaicking and denoising by total variation minimization［C］//2012 19th IEEE International Conference on Image Processing.IEEE，2012:2781-2784.

［7］ CHEN D，SUN S，ZHANG C，et al.Fractional-order TV-L2 model for image denoising［J］.Central European Journal of Physics，2013，11(10):1414-1422.

［8］ LI C，YIN W，ZHANG Y.User’s guide for TVAL3:TV minimization by augmented lagrangian and alternating direction algorithms［J］.CAAM report，2009，20:46-47.

［9］ RUDIN L I，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms［J］.Physica D:Nonlinear Phenomena，1992，60(1-4):259-268.

［10］ CONDAT L.Discrete Total Variation:New Definition and Minimization［J］.Siam Journal on Imaging Sciellles，2016，10(3):1258-1290.

［11］ CASELLES V，CHAMBOLLE A，NOVAGA M.Total variation in imaging［J］.Handbook of Mathematical Methods in Imaging，2015:1455-1499.

［12］ CHAMBOLLE A，POCK T.A first-order primal-dual algorithm for convex problems with applications to imaging［J］.Journal of Mathematical Imaging and Vision，2011，40(1):120-145.

［13］ BRESSON X，CHAN T F.Fast dual minimization of the vectorial total variation norm and applications to color image processing［J］.Inverse problems and imaging，2008，2(4):455-484.

［14］ CHEN P，HUANG J，ZHANG X.A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration［J］.Inverse Problems，2013，29(2):250-261.

［15］ LOU Y，YAN M.Fast L1-L2Minimization via a Proximal Operator［J］.Journal of Scicentific Compuig ，2016(1):1-19.