融合纹理特征与形状特征的病灶CT图像识别

高静雅，张荣国，赵 健，刘小君

(1.太原科技大学计算机科学与技术学院，太原030024;2.合肥工业大学机械工程学院，合肥230009)

近来，由于医学图像数据量十分巨大，仅仅依靠医务人员来进行分类工作，很多病变组织细节肉眼无法辨别，而且会夹杂着人对图像的主观性，导致效率十分低。为了提高医学分类的准确性、减少医务工作人员的工作量，辅助医生对病人的医学影像数据进行定量分析，对医学图像的二维影像进行进一步的处理成为目前研究的重点［1］。主要研究工作为如何利用图像处理技术，通过医学图像的各种特征，来对医学图像进行准确的分析，以此区别出正常和异常的医学图像。这样，既能提高图像识别检索的性能，还能帮助医生来进行辅助诊断，提高效率。

由于CT的密度分辨率高，对软组织的显示优于常规X线检查，且增强CT扫描检查，除能分辨血管的解剖结构外，还能观察血管与病灶之间关系，病灶部位的血供情况和血液动力学的变化。所以实验所选取的图像均为CT脑图，并选取纹理特征和形状特征作为主要的研究对象。图象纹理特征是图象区域内各象点空间结构关系的一种重要特征纹理特征大量用于图象分析和启动分类中，一直是图像领域研究的热点。其中，Haralick等人提出的灰度共生矩阵(Gray Level Co-occurrence Matrix，简称GLCM)以及洪继光的灰度梯度共生矩阵(Gray-Gradient Co-occurrence Matrix，简称GGCM)，在医学图像的识别有良好的应用，2012年NS Zulpe和VP Pawar［2］利用 GLCM 对脑肿图片进行分类，2013年曾宇凡［3］将GLCM用于肝纤维化的辅助诊断，2014年曾丽娟［4］使用GGCM对肛肠病症图像的分割和识别。形状特征选取hough变换后的特征和不变距特征。近年来的应用有，2014年DWR Paulus和V Seib［5］使用hough变换后的特征来识别物体，2015年R Varun和 YV Kini［6］用来进行面部识别。2015年LW Chen和CR Li［7］利用不变矩来进行指纹识别。

本文介绍一种基于纹理特征(GLCM、GGCM)和形状特征(hough变换后特征、矩特征)相结合，并采用SVM分类器对特征进行分类。

1 纹理特征

1.1 灰度共生矩阵

灰度共生矩阵［8］是一种综合信息，其主要针对于图像灰度在方向、相邻间隔、变化幅度这三个方面的信息表现。通过共生矩阵所得到的一些相应的特征值，这些特征值能够很好地反映出图像在纹理方面的信息。用 Pd(i，j)(i，j=0，1，2...L － 1) 来表示灰度共生矩阵，即某一灰度级为i的像素点沿某个特定方向θ到达距离为d、灰度级为j的像素点所出现的概率。其中，L为图像的灰度级，d为两像素之间的距离，θ表示方向。如果两个像素间的距离、方向等位置确定，则可以得到如下关系的灰度共生矩阵。

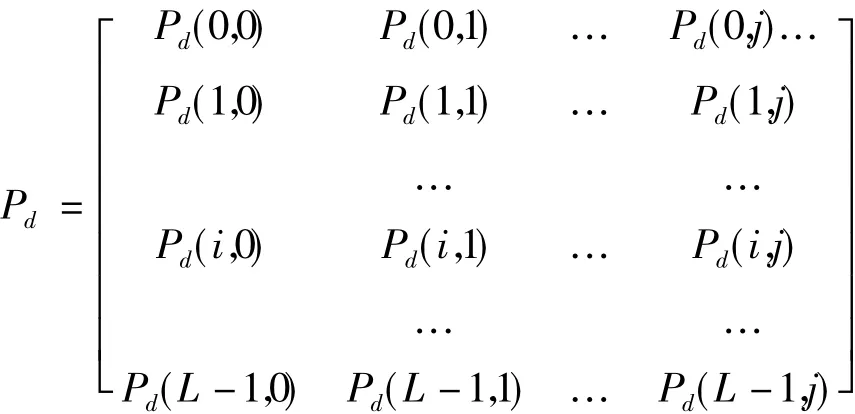
本文讨论实验中采用下面五个与灰度共生矩阵相关特征来提取医学图像的纹理特征。

(1)能量:

(2)对比度:

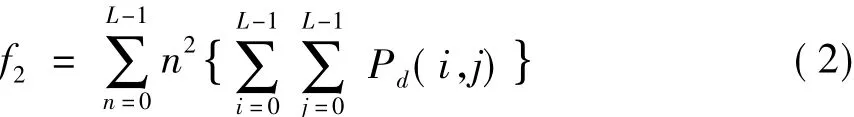
(3)逆差矩:

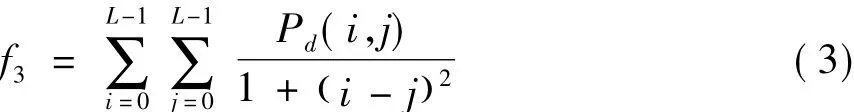
(4)熵:

(5)相关性:

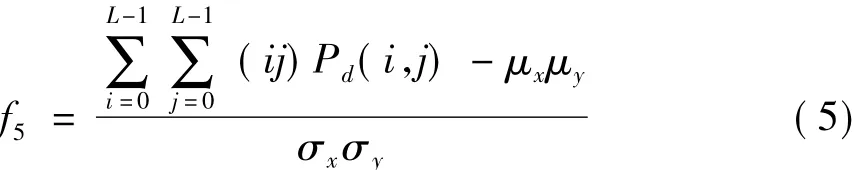
其中，μx，μy，σx，σy分别代表像素 x和y的均值和标准偏差。

1.2 灰度梯度共生矩阵

灰度梯度共生矩阵［9］在像素灰度的基础之上，结合边缘梯度的统计分布。因此两者的结合更能反映图像区域中细微纹理的变换。

(1)灰度分布的不均匀性:

(2)梯度分布的不均匀性:

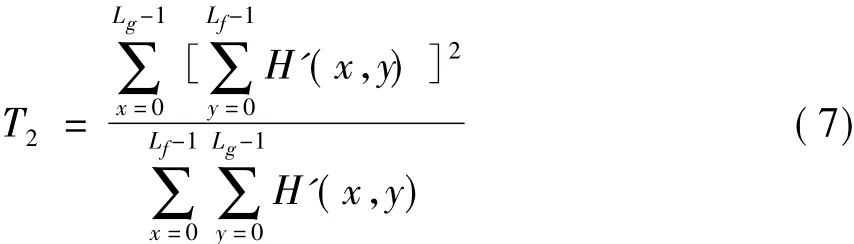
(3)灰度平均

(4)相关性:

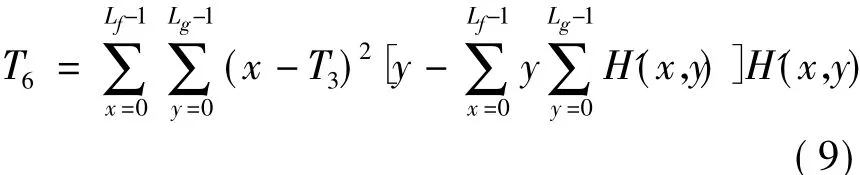
(5)惯性:

2 融合纹理特征与形状特征的SVM图像识别

用单一的纹理特征对医学图像进行分类时，可以反映图像灰度关于方向、相邻间隔、变化幅度的综合信息。但是如果对一些发生形变的病灶图像或者一些进行过平移旋转过的图像进行分类时，无法取得良好的分类效果。而基于Hough变换的特征和矩特征等的形状特征具有旋转、平移、缩放等不变的特性，可以很好地解决上述问题。

2.1 形状特征描述

2.1.1 基于Hough变换的特征

Hough变换是将图像空间的一点变换到参量空间的一条曲线或者一个曲面。因此具有相同参量特征的点，在经变换后可以在参量空间中相交。

其中，ρ是表示了由直线至原点的法线距离，θ则是该法线与x的夹角。因此可由如下方程来表示该直线:

主要步骤如下:

Step1:将图像进行hough变换;

Step2:将变换后的图像利用垂直方向的差分运算得到总的像素能量

Step3:得到单位像素能量特征E=H/［X(Y－2)］

2.1.2 矩特征

矩特征具有旋转、尺度、平移等的不变特征。因而在图像处理中，矩特征可以作为一个重要的特征指标来表示出物体的特征信息。所以利用矩特征来对图像进行分类时，不会因图像在采集之后出现因旋转、平移等畸变带来的图像失真影响而造成所提取的特征值的改变。

对于二值图像I(x，y)的(p+q)阶矩阵定义为:

图像的二阶几何矩 m02，m20，m11，成为惯性矩，他们可以用来表示图像的特征，且计算较为简单，可适用于较为复杂的图像。本实验中仅用其中的m11作为特征值。

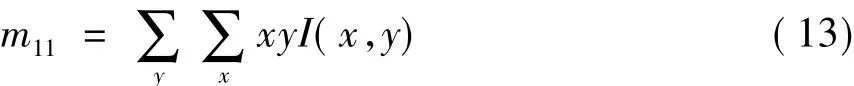
2.2 融入两类特征的SVM分类

所提取的纹理特征和形状特征组成的图像特征为非线性的。在这种情况下，学习样本是线性不可分，但却是非线性可分的情况下，可以通过非线性变换把学习样本变换到高维空间，使其在高维空间里是线性可分的。将原来的点积(x·y)通过核函数K(x，y)代替。Mercer定理中提到核函数K(x，y)能够通过与其相联系的非性变换φ，隐含地将特征向量从而映射到高维特征空间中。这样使得非线性的学习样本变为线性可分的。对与这种非线性问题，线性分界面的分类能力可能无法达到满意的结果，可通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题:φ(x):R→dE将数据映射到更高维的特征空间E中，则该特征数据就变成线性可分，然后再在E中构造最优或广义最优分类超平面。因为无论是分类函数还是优化函数，全部只涉及样本间的内积运算。所以在变换后的高维空间E中，仅仅需要内积运算φ(xi)·φ(xi)。根据泛函的有关理论，如果函数K(xi，yj)满足Mercer条件，则它对应某变换空间中的内积，即(φ(xi)·φ(xi))=K(xi，x)。因为对偶形式就是线性学习器的一个重要性质，所以假设可以表达为训练点的线性组合。其中，样本特征值为xi，测试特征值为x，则决策规则能够用测试点和训练点的内积表示:

在不增加计算复杂度的情况下，实现某一非线性变换后的线性分类。此时优化函数变为:

相应的判别函数为:

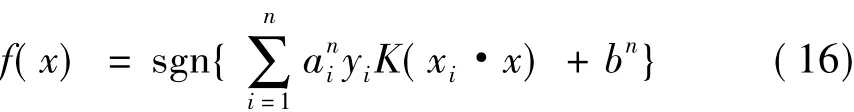
综上，选取SVM作为进行分类器是一个很好的选择。SVM［10］(Support Vector machine，支持向量机)这种分类方法在解决非线性小样本识别中表现出诸多优势。尤其在查全率和查准率方面，SVM方法基本上超过了大部分的现存的所有方法。

有关两类的分类问题，原始问题为:

约束条件:yi(wTwφ(xi)+b )≥1 － εi;εi≥0;

i=1，...，n.其中，数据点所属的类别用xi∈ Rn;

y∈{1，－1}l来表示;w为与最优分类面垂直的向量;C为惩罚因子;εi为系数变量。

本文选用的支持向量机类型为C-SVC.选用径向基核函数(RBF核函数):K(x，y)=exp(－γ‖x－y‖2)进行实验。

2.3 算法总流程

图1 算法总流程图Fig.1 Flow chart of algorithmt

3 实验与结果分析

为验证本文所提出的方法，使用50幅CT脑图来进行小样本的分类实验。其中包含:25幅脑出血图片，25幅正常脑图。每幅图像像素为512*512.实验均在Pentium(R)Dual-Core CPU 2.10 GHz，2.46 GB RAM计算机上通过MATLAB和LibSVM平台实现。图2中(a)列为正常脑图(b)列为病变脑图。

图2 正常脑图与病变脑图Fig.2 Normal brain images and lesion brain images.

表1-表3随机选取了从6幅脑图所提取的特征信息。

3.1 分类实验

3.1.1 实验一

首先将50幅图片进行预处理，然后分别提取其纹理特征与形状特征，纹理特征提取灰度共生矩阵的5个特征值:能量、对比度、逆差矩、熵、相关以及灰度梯度共生矩阵的5个特征值:灰度分布的不均匀性、梯度分布的不均匀性、灰度平均、相关、惯性;形状特征提取基于Hough变换的特征E和二阶矩特征中的m11，以上值作为50组特征值。然后将这50组特征值作为训练集将其利用libsvm软件包形成模型。最后再将这50组特征值作为于预测集放入模型进行识别。结果如下(分类精确率):

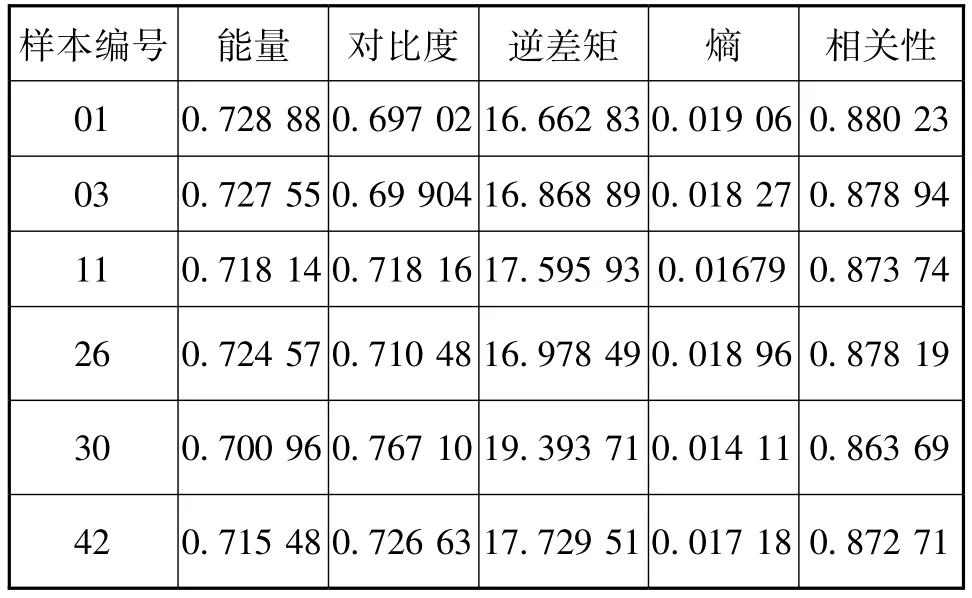
表1 脑图纹理特征GLCM参数Tab.1 GLCM textures feature parameters of brain images

表2 脑图纹理特征GGCM参数Tab.2 GGCM textures feature parameters of brain images

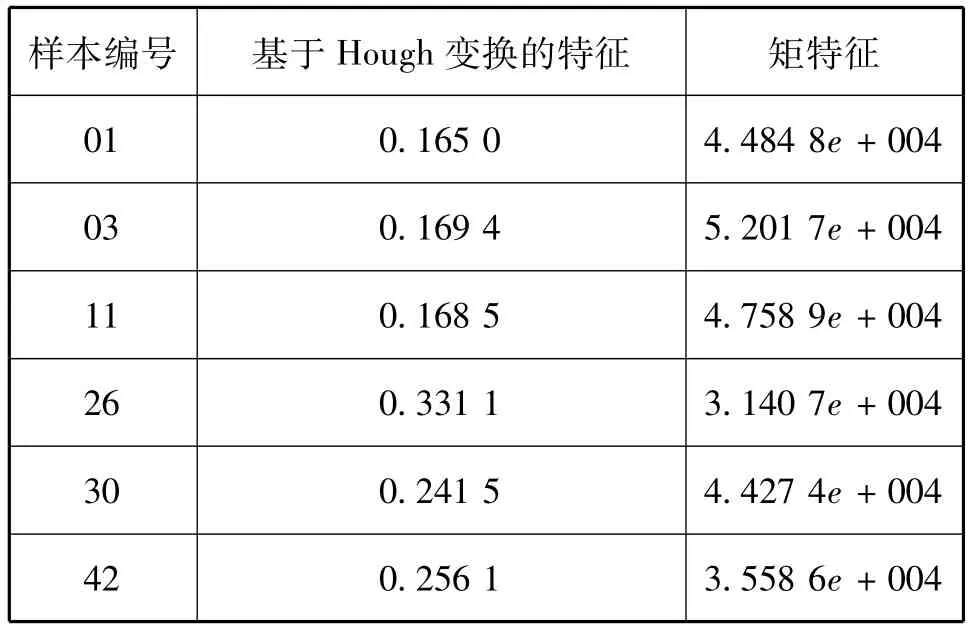
表3 脑图形状特征参数Tab.3 Shape characteristic parameter of brain images

表4 实验一分类结果Tab.4 Classify results of experiment one

3.1.2 实验二

首先取40组特征值作为训练集形成模型，再用剩余的10组特征值(正常脑图病变脑图的特征值各5组)作为预测集来进行预测分类，一共抽取5次，取5次分类结果的平均值。其结果如下(分类精确率):

表5 实验二分类结果Tab.5 Classify results of experiment two

3.2 结果分析

从表4中可知，加入基于Hough变换的特征E和二阶矩特征中的m11分别到GLCM和GLCM中均有很好的识别效果，分类的精确率达到100%.而仅仅利用GLCM和GLCM特征值进行分类时，分类结果仅为74%和70%.当医院中的大量图像数据不易进行分类管理时，可以使用此分类方法对现有的图像进行很好的识别。这种方法还可以应用到公司内部的面部识别系统，将面部纹理特征和形状特征作为一组特征值从而进行很好的识别作用。

从表5中可知，预测分类精确率的由高到低排列依次为:GLCM ＞GGCM+E+m11＞GLCM+E+m11＞GGCM.GLCM特征值的预测分类效果最好为64%.GGCM特征值的预测分类效果最差，仅为24%.基于Hough变换的特征E和二阶矩特征中的m11分别与GLCM和GLCM特征值结合效果处于以上两者之中。但是，只观察病变脑图分类精确率可知，本文方法的分类精确率最高。总共5组病变脑图中，分别识别出病变脑图为4和5幅，病变脑图的分类精确率分别为80%和100%.

4 结论

利用计算机辅助诊断对医学病灶图像与正常图像进行有效地分类识别已经成为目前研究热点［11］。计算机辅助诊断对病灶的特征提取和图像分类这两个方面，显得十分重要。从实验一的结果看，将50组含有纹理特征和形状特征作同时为训练集和预测集，可以达到100%的识别精确率。此种分类方法除了应用于对大量医学图像进行分类和管理，还可以应用在公司内部的面部识别系统以得到良好的识别效果。实验二的结果来看，40组作为训练集10组作为预测集，将纹理特征和形状特征一起作为特征值进行分类时，在识别正常脑图效果欠佳，接下来的实验对此还需要进行进一步改进。本实验选取小样本的医学CT图像进行实验，后续的研究中还可以增加样本数目，进行更好的完善。

参考文献:

［1］ 付燕，聂亚娜，靳玉萍.基于SVM的肝脏B超图像纹理分类［J］.计算机应用与软件，2012，23(4):291-294.

［2］ NS ZULPE，VP PAWAR.GLCM textural features for Brain Tumor Classification［J］.International Journal of Computer Science Issues，2012，9(3):354-359.

［3］ 曾宇凡.基于医学图像的肝纤维化计算机辅助诊断研究［D］.广西:广西大学，2013.

［4］ 曾丽娟，张华，彭洪云.基于支持向量机的肛肠病症识别算法研究［J］.计算机仿真，2013，30(11):343-346.

［5］ DWR PAULUS，V SEIB，M KUSENBACH.Object Recognition Using Hough-transform Clustering of SURF Features［J］.Workshops on Electronical＆ Computer Engineering Subfields，2014，10(16):176-183.

［6］ R VARUN，YV KINI，K MANIKANTAN.Face Recognition Using Hough Transform Based Feature Extraction ［J］.Procedia Computer Science，2015，46:1491-1500.

［7］ LW CHEN，CR LI.Invariant moment features for fingerprint recognition ［J］.International Computer Conference on Wavelet Active Media Technology ＆ Information Processing，2013，6(3):91-94.

［8］ HARALICK R M，SHANMNGAM K，DINSTEIN.Texture feature for image classification［J］.IEEE Transactions on Systems，Man and Cybernetics，1973，3(6):768-780.

［9］ 洪继光.灰度-梯度共生矩阵纹理分析方法［J］.自动化学报，1984，10(1):22-25.

［10］ CORTES C，VAPNIK V.Support-vector networks［J］.Machine Learning，1995，20(3):273-297.

［11］ 任美美，张荣国，胡静，等.融入光度信息图割的图像轮廓提取方法［J］.太原科技大学学报，2015，36(2):103-108.