求解无约束优化问题的非单调自适应信赖域方法

徐明明

（成都理工大学，四川 成都610059）

1 概述

传统的求解无约束优化问题的迭代方法是行搜索方法或信赖域方法。很多学者通过改进信赖域半径以及非单调项来提高信赖域方法的鲁棒性以及加快收敛速度。

2 问题的提出

考虑无约束优化问题：

在传统信赖域方法中，通过解决以下子问题，选择一个试验步骤dk：

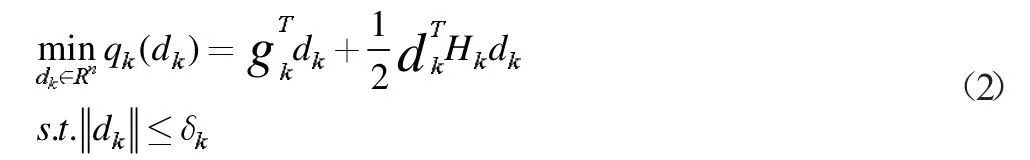
其中gk∈Rn和Hk∈Rn分别是在当前迭代点xk处f（x）的梯度和Hessian 矩阵的近似。||·||是欧氏范数，δk>0 是当前迭代点的信赖域半径。

3 新的非单调自适应信赖域方法

在这一部分中，提出了一种新的非单调自适应信赖域算法，该算法是基于文献[1]中提出的非球面信赖域半径与文献[2]中提出的一种新的非单调比率。

在文献[1]中，作者提出了一种非球面信赖域的非单调信赖域算法。

首先，介绍了一种基于Hessian 矩阵在当前迭代点的特征值，然后将非单调搜索策略与信任区域方法相结合。其算法如下：

将λki设置为在迭代点xk处Hessian 矩阵Hk的第i 个特征值。通过Ger觢gorin Circle theorem，得到：

然后，在迭代点xk处的第i 维中的非球面信赖域的尺度可以由

确定。也就是说，试验步骤dk在（2）中的第i 个元素dki在[-δki，δki]中是有界的。

利用（4），可以将球面信赖域转换为非球面信赖域。因此，子问题（2）转换为

为了进一步调整信赖域，引入了以下两个参数：

为了提高信赖域算法的计算效率以及增强收敛性，文献[2]提出来一种新的非单调项：

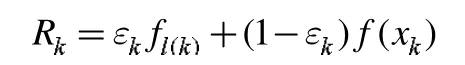
其中

其中是满足下列条件的正序列：

信赖域比率如下：

基于以上两种方法，本文提出了新的信赖域算法：

Step3：在迭代点xk处求解子问题（5）。

Step4：计算fk+1，通过（4）计算δki，

Step6：令xk+1=xk+dk，mk=min{k，M}，k：=k+1 转Step2。

4 结论

本文提出的新的非单调自适应信赖域算法，是文献[1]与文献[2]的优点的一个融合。以后，会对本算法进行进一步的研究。