对高中物理解题方法的认识

安子正

(保定市第三中学 河北 保定 071000)

下面主要对几种常见的物理解题方法进行分析．

1 微元法

(1)装置从释放到开始返回的过程中，线框中产生的焦耳热Q；

(2)线框第一次穿越磁场区域所需的时间t1；

(3)经过足够长时间后，线框上边与磁场区域下边界的最大距离xm．

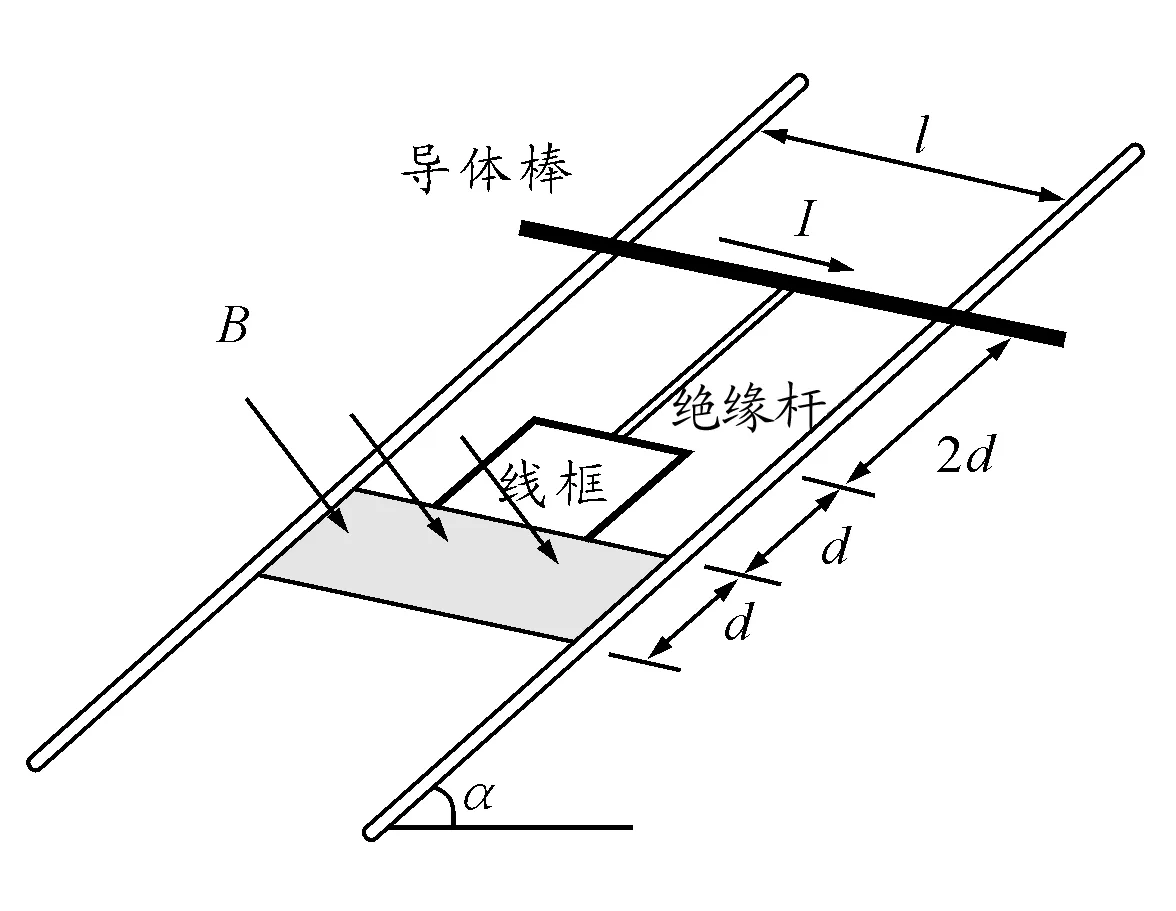
图1 例1题图

解：(1)设装置由静止释放到导体棒运动到磁场下边界的过程中，作用在线框的安培力做功为W，由动能定理

mgsinα·4d+W-BILd=0

且Q=-W

解得

Q=4mgdsinα-BILd

(2)设线框刚离开磁场下边界时的速度为v1，则接着向下运动2d，由动能定理

装置在磁场中运动的合力

F=mgsinα-F′

感应电动势ε=Bdv

安培力F′=BI′d

由牛顿第二定律，在t到t+Δt时间内，有

则

有

(3)经过足够长时间后，线框在磁场下边界与最大距离xm之间往复运动，由动能定理

mgxmsinα-BIL(xm-d)=0

2 待定系数法

【例2】已知数列{an}满足a1=5，a2=5，an+1=an+6an-1(n≥2)．

(1)求证：{an+1+2an}是等比数列；

(2)求数列{an}的通项公式；

(3)设3nbn=n(3n-an)，且|b1|+|b2|+…+

|bn|

(1)由

an+1=an+6an-1

an+1+2an=3(an+2an-1)(n≥2)

因为

a1=5a2=5

所以

a2+2a1=15

故数列{an+1+2an}是以15为首项，3为公比的等比数列.

(2)由(1)得an+1+2an=5·3n

由待定系数法,可得

(an+1-3n+1)=-2(an-3n)

即an-3n=2(-2)n-1

故an=3n+2(-2)n-1=3n-(-2)n

(3)由

3nbn=n(3n-an)=n[3n-3n+(-2)n]=n(-2)n

所以

令

Sn=|b1|+|b2|+…+|bn|

要使得|b1|+|b2|+…+|bn|

3 分类讨论法

【例3】如图2(a)所示，绝缘水平面上相距L=1.6 m的空间内存在水平向左的匀强电场E，质量m=0.1 kg，带电荷量q=1×10-7C的滑块(视为质点)以v0=4 m/s的初速度沿水平面向右进入电场区域，滑块与水平面间的动摩擦因数μ=0.4(设最大静摩擦力与滑动摩擦力相等)．(g取10 m/s2)

(1)如果滑块不会离开电场区域，电场强度E的取值范围多大．

(2)如果滑块能离开电场区域，试在W-F坐标中[图2(b)]画出电场力对滑块所做的功W与电场力F的关系图像．

图2 例3题图

解:(1)小滑块在摩擦力和电场力的作用下，向右做匀减速直线运动，设加速度为a，依题意和牛顿第二定律，有

F+f=ma

(1)

又F=qE

(2)

f=μmg

(3)

若小滑块不会从右侧离开电场区域，由匀变速直线运动规律，有

(4)

联立式(1)～(4)并代入数据得

E>106N/C

(5)

若小滑块不会从左侧离开电场区域，必须满足

F≤f

(6)

联立式(2)、(5)、(6)可得

106N/C

(7)

(2)如果小滑块会离开电场区域，电场力F必须满足

F=qE=q=1×10-7×106N≤0.1 N

(8)

或F=qE= 1×10-7×4×106N>0.4 N

(9)

若F≤0.1 N，小滑块将从右侧离开电场区域，此过程小滑块在电场中的位移s=1.6 m，则电场力做功

W=-Fs=-1.6F

(10)

若F>0.4 N，小滑块将从左侧离开电场区域，此过程小滑块在电场中的位移s=零，电场力做功为零，即W=0.

作图后W-F关系图像如图3所示.

图3 作图后W-F关系图像

4 图像法

【例4】一颗速度较大的子弹，水平击穿原来静止在光滑水平面上的木块，设木块对子弹的阻力恒定，则当子弹入射速度增大时，下列说法正确的是( )

A．木块获得的动能变大

B．木块获得的动能变小

C．子弹穿过木块的时间变长

D．子弹穿过木块的时间变短

图4 例4题图

解析：子弹以初速穿透木块过程中，子弹、木块在水平方向都受恒力作用，子弹做匀减速运动，木块做匀加速运动，子弹、木块运动的v-t图如图4中实线所示，图中OA，v0B分别表示子弹穿过木块过程中木块、子弹的运动图像，而图中梯形OABv0的面积为子弹相对木块的位移即木块长．当子弹入射速度增大变为v0时，子弹、木块的运动图像便如图中虚线所示，梯形OABv0的面积仍等于子弹相对木块的位移即木块长，故梯形OABv0与梯形OABv0的面积相等，由图可知，当子弹入射速度增加时，木块获得的动能变小，子弹穿过木块的时间变短，所以本题正确答案是B，D.