载流圆线圈磁场的MATLAB数值计算

程 军

(安徽信息工程学院基础教学部 安徽 芜湖 241000)

从理论的角度来说，利用毕奥-萨伐尔定律原则上可以给出任意形状的载流导线在空间产生的磁场．但是，在实际计算过程中，如果载流导线的形状不规则，一般情况下无法给出磁感应强度的解析形式，此时可以利用数值计算方法来求解载流导线的磁场．MATLAB是进行数值计算的强大工具，将其应用于物理教学过程中，不仅能够提升教学效果，还可以激发学生学习物理的兴趣，并且提高学生分析和解决问题的能力．本文利用MATLAB数值计算，对载流圆线圈的磁场进行求解．

1 载流圆线圈的磁场

如图1所示，半径为R，通有逆时针方向电流I的圆线圈处于xy平面内，且其圆心在原点O．在线圈上与x轴正向夹角为α处取一电流元Idl，即

Idl=IRdα(-isinα+jcosα)

(1)

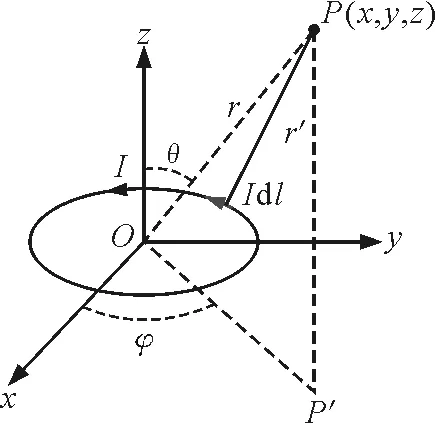
图1 载流圆线圈

该电流元Idl的位置坐标为

x′=Rcosα

y′=Rsinα

z′=0

(2)

空间任一点P(x,y,z)可用球坐标表示为

x=rsinθcosφ

y=rsinθsinφ

z=rcosθ

(3)

因此，由电流元Idl引向场点P的矢量为

r′=(x-x′)i+(y-y′)j+zk

(4)

根据毕奥-萨伐尔定律，载流圆线圈在P点产生的磁感应强度为[1]

(5)

由式(1)～(5)，可得磁感应强度的分量分别为

(6)

(7)

(8)

根据电流分布的轴对称性可知，磁场分布也具有轴对称性，不妨取P点在xz平面内．因此，由式(6)～(8)可简化为

(9)

(10)

(11)

特殊地，当P点位于圆线圈轴线上时，磁感应强度为

(12)

2 MATLAB编程求解

根据毕奥-萨伐尔定律，原则上可以求解任意形状的载流导线在空间产生的磁场．但是对于形状不规则的载流导线，通常无法给出磁感应强度的解析形式．此时，我们可以借助MATLAB程序对磁感应强度进行数值积分求解[2]．

计算载流圆线圈的磁场所用的MATLAB程序如下：

I = 1; R = 0.1;

n1 = 5; n2 = 6;

r = [0.05,0.15,0.3,0.5,1.0];

t = [0,10,30,45,60,90];

B = zeros(n1,n2); s = zeros(1,n2);

n = 1000; h = 2*pi/n; x = [0:h:2*pi];

for i = 1:n2

s(i) = t(i)*pi/180;

end

for i = 1:n1

for j = 1:n2

Bx = 0; By = 0; Bz = 0;

for k = 1:n

Bx = Bx+I*R*r(i)*cos(s(j))*

cos(x(k))./(R.^2+r(i).^2-2*R*r(i)*

sin(s(j))*cos(x(k))).^(1.5)*h;

By = By+I*R*r(i)*cos(s(j))*

sin(x(k))./(R.^2+r(i).^2-2*R*r(i)*

sin(s(j))*cos(x(k))).^(1.5)*h;

Bz = Bz+I*R*(R-r(i)*sin

(s(j))*cos(x(k)))./(R.^2+r(i).^2-2*R*

r(i)*sin(s(j))*cos(x(k))).^(1.5)*h;

end

B(i,j) = sqrt(Bx.^2+By.^2+Bz.^2);

end

end

在计算中取圆线圈半径0.1 m，通有电流1 A．根据上述MATLAB程序，求解特定的空间位置处的磁感应强度，如表1所示．特殊地，线圈圆心处的磁感应强度大小为6.283×10-6T．

表1 特定空间位置( r, θ )处磁感应强度的大小 (单位：×10-7 T)

3 总结

本文根据毕奥-萨伐尔定律和磁场叠加原理，给出载流圆线圈在空间产生的磁感应强度计算公式的一般形式，利用MATLAB编程对磁场进行数值计算，并且给出一些特定空间位置处的磁感应强度的大小．将MATLAB应用于大学物理教学，有助于提升教学效果，提高学生学习物理的积极性，并且可以培养探索和求解物理问题的能力．

参 考 文 献

1 贾起民，郑永令，陈暨耀.电磁学.北京：高等教育出版社，2009.161～163

2 王健，赵国生.MATLAB数学建模与仿真.北京：清华大学出版社，2016.357～359