载流螺线环磁场的MATLAB仿真*

周鑫 李江珊 吴明和 滕保华

(电子科技大学英才学院 四川 成都 611731)(电子科技大学物理学院 四川 成都 610054)

1 引言

对于载流圆线圈和长直载流螺线管的磁场，无论是数学推导[1，2]、还是模拟仿真[3，4]，在教科书和文献中已经有了详尽的介绍和描述．然而关于载流螺线环磁场的分析却比较少见[5]，既缺少对载流螺线环磁场的数学分析，也缺少对螺线环磁场的仿真计算．本文基于载流圆线圈的磁场，分别利用毕奥-萨伐尔定律和磁矢势计算了不同密绕程度下载流螺线环的磁场分布，并利用MATLAB对载流螺线环的磁场进行了数值仿真，揭示了磁场随距离、方位角度以及密绕程度的变化特征．

2 计算方法

下面分别从毕奥-萨伐尔定律[6，7]和磁矢势[8]出发，计算不同密绕程度的载流螺线环的磁场．在计算时，螺线环中的每匝线圈用载流圆线圈代替，即螺线环的匝数就是圆环的个数，并且不考虑载流导线的直径．

2.1 基于毕奥-萨伐尔定律的计算

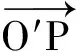
图1 载流螺线环磁场示意图

在图1中，O′为螺线环上任取的一个载流圆线圈的圆心，φ为任一电流线圈平面上线圈圆心到电流元的矢量r1与电流线圈平面极坐标的极轴的夹角，容易得到圆线圈上任一电流元到P点的位置矢量为

r3=x-R1cosα-r1sinφcosαex+

y-R1sinα-r1sinφsinαey+

(z-r1cosφ)ez

而圆环上的电流元为

Ir1dφeτ

其中eτ表示在圆电流线圈的切向方向上的单位向量，则载流圆线圈在P点的磁感应强度为

(1)

从而载流螺线环在任一点P(x,y,z)的磁场强度为

(2.1)

(2.2)

(2.3)

2.2 基于磁矢势的载流螺线环磁场的计算

参考平面上方位角α处的载流圆线圈在P点的磁矢势可以表示为[8]

Ar2,θ,φ,α=Ar2,θ,φeφ=

(3)

进而由B=×A可以得到P点磁感应强度

Bα=Br2αer2+Bθαeθ+Bφαeφ

(4)

其中

eφ=er2×eθ

注意B(α)是α的函数，P点总磁感应强度B等于所有不同α处的圆电流对P点贡献的磁感应强度B(α)累加，即

(5)

其中

(6.1)

(6.2)

(6.3)

比较以上两种不同对螺线环磁场的计算方法可以发现，不管是基于毕奥-萨伐尔定律还是基于磁势矢的计算方法，均物理概念明确，数学计算规范，而且便于仿真．

3 仿真分析与讨论

以螺线环半径r1=10 m，载流圆线圈半径R1=3 m,电流I=1 A的螺线环为例，仿真不同密绕程度下载流螺线环的磁场分布．

3.1 磁场分布的整体特征

在匝数N=50，100，200等3种密绕程度下，利用MATLAB仿真了其磁场的整体分布．可以看出，当N较小时，毛刺现象严重；随着密绕程度增加，螺线环的磁场变化越来越平滑．当N=200时，螺线环的磁场分布可近似为理想螺线环的分布，即磁场呈圆对称分布，只有螺线环内部存在磁场．

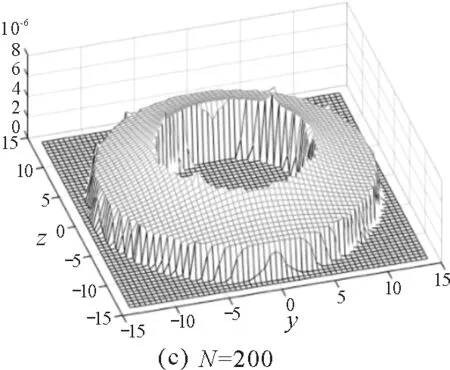
图2 3种情况下载流螺线环的磁场分布

3.2 磁场与距离的跃变特征

在螺线环参考平面上且方位角为零，计算了距离圆心任意距离处的磁场，图3为MATLAB仿真的结果．

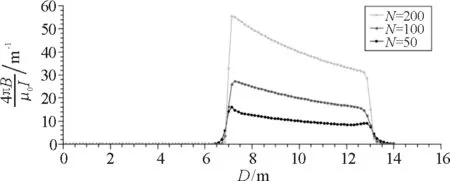
图3 3种情况下载流螺线环的磁场跃变特征

可以看出，磁场分布呈现跃变性的特点，即在螺线环范围之外的区域磁场几乎为零，而在螺线环内磁场与离圆心的距离成反比关系．但当密绕程度低时，跃变不明显，边缘处缓慢上升或下降；当密绕程度高时，边缘处陡升或陡降的跃变特征明显．

3.3 磁场与角度的周期特征

在螺线环参考平面且在螺线环内半径为9 m一个圆周上，计算了各点的磁场大小，其MATLAB仿真的结果如图4所示，其中显示出磁场分布随角度变化的周期性．

图4 磁场随角度的变化关系

3.4 磁场与密绕程度的振荡特征

在螺线环参考平面上，且在螺线环内半径为12.5 m，方位角为零的一个固定位置，计算了密绕程度从N=0～150不同情况下，该固定点磁场的MATLAB仿真结果如图5所示．从图5可明显看出，随着密绕程度上升，该点的磁场大小呈总体上升的振荡特征．

图5 磁场随密绕程度的变化关系

实际上，整体的上升性是由于随着螺线环密绕程度的提高，螺线环的漏磁现象减弱，从而使得螺线环内部的磁场变大；而振荡性则是由于随着螺线环密绕程度的变化，该固定点与各个载流圆环的相对位置发生了往复变化，导致磁场叠加的结果是振荡的．

4 结论

本文分别从毕奥-萨伐尔定律和磁矢势出发，计算不同密绕程度的载流螺线环的磁场，并利用MATLAB仿真，得到了载流螺线环的磁场分布，从而对不同密绕程度情况下磁场分布呈现的跃变性、周期性、以及振荡性等特点加深了认识．