柔顺杆大变形分析的A-T-S方法

杨鹏飞，张学良，权 诺，侯晓丹

(太原科技大学机械工程学院，太原030024)

包含柔顺杆连接的柔顺机构有很多潜在的优点，与传统的机构相比，它积极地利用构件自身的变形来传递运动、力和能量，具有减少构件数量，节约装配时间、简化加工程序、避免摩擦和噪音等优点[1]。目前对柔顺杆的分析更多的集中在对等截面柔顺杆的简化和精确分析中，文献[2]应用椭圆积分方法来计算柔顺杆受力和位移、角度之间的关系，但其方法复杂 、计算难度大，且只能表示杆的末端运动情况。在柔顺机构的简化分析中，HOWELL[3-5]、SU[6]、冯忠磊[7]等分别提出了1R、3R和2R伪刚体模型，在柔顺杆的分析中各有优劣，但其误差较大，适合于柔顺杆的简化分析。Howell, Midha等[8-9]在对构件分类时，提出段的直观概念，将构件由于横截面的不同区分为若干段，并分析了柔顺杆的段与段的自由度、以及段间的连接类型情况，提出了一个柔顺段的划分及柔顺机构自由度计算的标准。对于分析柔顺机构时使用的Adams方法，王英慧等[10，11]进行了研究。L.Saggere等[12]提出了一种数值方法对柔顺杆进行分析，如图1，针对末端受力F和同向力矩M0的柔顺杆，将其用多个刚杆和刚度为EI/L的扭簧相连接的等长小段模型来代替(Model of curved beam using torsional springs and rigid elements简称T-S模型)，然后对各段之间的受力参数进行拟合，进而达到近似计算杆末端以及杆各部位变形情况的目的，但是其拟合难度较大，计算过程中需同时满足运动学和静力学平衡约束，导致当分段数较大时，其计算速度变得很慢，文中用此方法通过杆末端的位移和角度变化来反向设计柔顺杆。综上所述，当前对杆状柔顺机构的研究包括应用椭圆积分对其末端运动情况的研究、应用伪刚体方法对其末端运动状况的近似研究等，而此类方法并不能精确得出柔顺杆受力和力矩后各部分的应变能、变形、受力等情况。

本文对T-S模型进行了改进，由一系列的刚性杆和刚度为EI/L的扭簧来等效替代柔顺杆，进而对其进行大变形分析。将其对杆的分段方法由T-S模型中按杆长平均分段化为了按末端转角分段，每段杆相对于上一段杆的相对转角为固定值，得出了一种新的t-s模型(Model of curved beam using torsional springs and rigid elements which devided by angle, 简称A-T-S模型)，如图2.根据相对转角固定推出了相邻两杆的长度之间的关系，再利用杆右边界所受力矩为集中力矩M0的边界条件，通过数值搜索得出合适的杆长组合，进而得出杆末端转角和所受力之间互相计算的方法。最后与椭圆积分算法进行了对比，验证了此方法的可行性,从而为柔顺杆的分析及设计提供了一种新的思路和方法。

图1 末端受力柔顺杆及其T-S模型
Fig.1 The compliant bar with tip load and its T-S model

1 A-T-S模型

如图2(a)所示，研究对象为末端受到集中力和同向力矩的均质柔顺杆，其杆长为L0，杆的弹性模量为E，惯性矩为I.杆受到纵向力P，横向力n×P和末端力矩M0后变形情况如图中实线所示，变形前杆位置如图中虚线所示。受力后末端转角为θ°，右端点的横向坐标为a，纵向坐标为b，所受力矩M0和力P的关系为M0=P*K1*L0,(K1用以表示末端受力和力矩对杆变形的贡献率[7])。

分析模型如图2(b)所示，将柔顺杆设为多个刚杆和扭簧的组合，利用T-S模型，设第i段的扭簧刚度为W=E*I/Li，其中E为杆弹性模量，I为杆的惯性矩，Li为第i段的长度。对T-S模型进行了改变，每段杆长不再相等，而是假设每一段相对上一段的相对扭转角度都一样。每段的左端点所受的力矩分别用Mi来表示，则第一段在复合力F的作用下扭转角度为Φ，于是对第一段有等式(1)：

图2 自由端受力的柔性梁及其A-T-S模型
Fig.2Acompliantbeamwithatiploadandasamedirectionmomentwithit’sA-T-Smodel

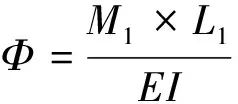
(1)

同理对第2、…和第i、m段有等式(2)：

(2)

…

(3)

…

(4)

相邻两段之间的力矩差为：

M1-M2=P×L1×cosΦ1+nP×L1×sinΦ1

(5)

…

Mi-1-Mi=P×Li-1×cosΦi-1+

nP×Li-1×sinΦi-1

式中，M为FFT点数，l=Round(2NMvΔfTr/c)，继续对s(i)作FFT后归一化取模，可得

(6)

…

Mm-1-Mm=P×Lm-1×cosΦm-1+nP×Lm-1×sinΦm

(7)

连列式(1)- (7)得：

(8)

…

(9)

…

(10)

于是当分段数趋于无穷时各杆长L之和满足：

(11)

根据边界条件，杆最末端所受力矩为M0，于是当分段数趋于无穷时有：

nP×Li×sinΦi)-M0=0

(12)

其中Φi=Φ×i

(13)

于是由式(1)、式(7)-(12)可得到一个n+2元非线性方程组。当已知末端转角和末端对上面所得的方程组求解，得到其满足精度的解即可得到每小段杆的长度和末端受力P的值，进而可得到杆各个部分的位移、变形和储能状况以及各部分所受力的大小。

2 模型求解

2.1 目标函数及约束定义

nP×Li×sinΦi)-M0|

(14)

s.tLi=

(i=2、3…m)

(15)

(16)

(17)

2.2 求解流程

3 算例验证

3.1 末端轨迹误差分析

当用A-T-S方法获得了最佳杆长度向量之后，杆末端的轨迹可以用累加得到，公式如下：

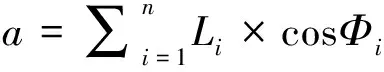
(18)

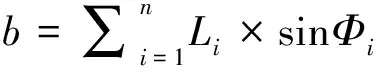
(19)

取一参数已知的杆为研究对象，其几何和物理参数如下：各材料均为柔性钢梁，其弹性模量E=30×106 N/cm2,长L0=20 cm，宽w=1.25 cm以及高h=1/32 cm，即惯性矩I=3.28×10-6cm4，横纵方向受力比为1，在末端转角不同时，对末端轨迹和末端受力进行计算，椭圆积分和A-T-S方法的比较结果如图4.

如图4(a)所示，随着分段数的增加，A-T-S方法对末端位移计算所得的结果越来越接近于传统椭圆积分的计算结果。

定义伪刚体模型末端变形位置与柔顺杆的末端变形位置的距离和柔顺杆原长L0之比为相对变形误差e来衡量伪刚体模型对柔顺杆的模拟效果。相对变形误差公式为[7]:

(20)

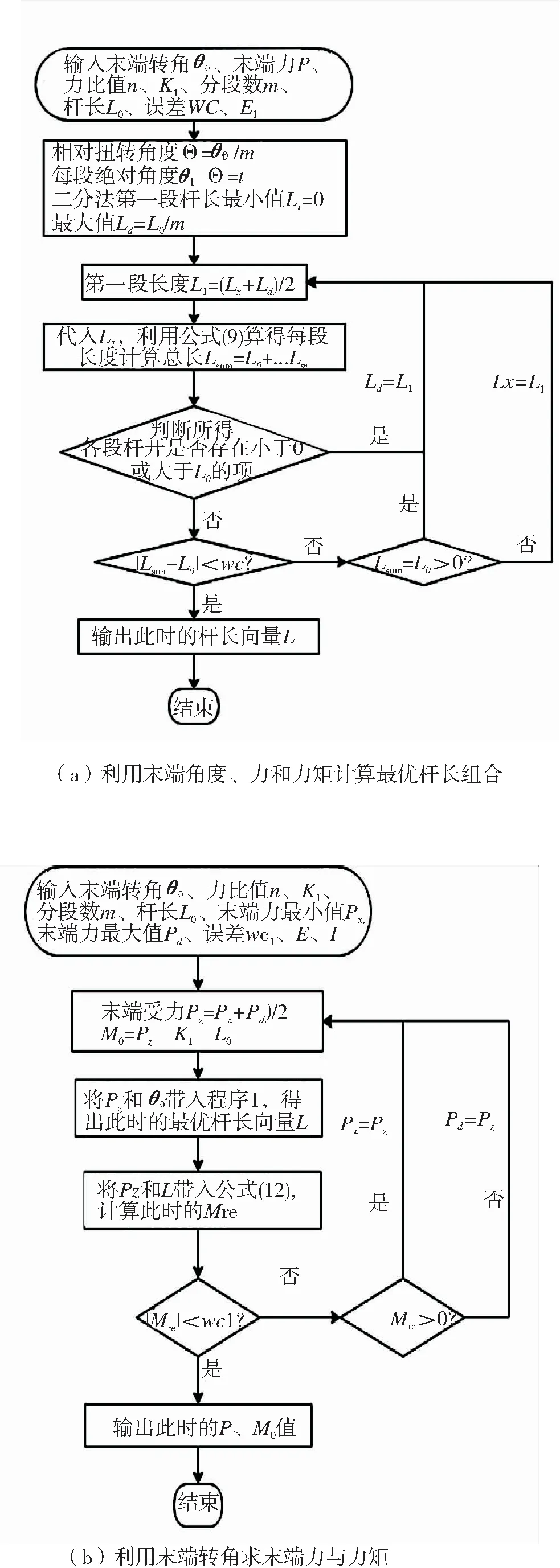
图3 模型求解流程图
Fig.3 The flow chart of the model’s solution process

于是得出图4(b),由图可得，当分段数为10 000时，在末端转角不大于134°(此受力下极值角135°)，杆长和力F近似误差限定在10-5时，最大相对变形误差e小于0.1%，末端力F的相对计算误差小于0.5%.而当分段数为100 000时，经计算得，最大变形误差e小于0.03%，力F相对计算误差小于0.07%，且其误差随着分段数的增加而不断减小。

3.2 大变形柔顺杆的应变能分布情况

对末端受力矩的大变形柔顺杆，其每一段的应变能可用下式计算：

(21)

其中Wi为第i段的扭簧刚度。

于是对上述大变形柔顺杆，当其末端转角为90°时，利用公式(20)及利用A-T-S方法累加，输出了其应变能沿着杆长位置的变化情况如图5所示：

由图5可得，变形能随着杆长的增大，逐步变大，但其趋势越来越平缓，这是由于越接近右端，力对杆的力矩越小的原因，在此情况下计算得杆的总变形能为8.44 N·cm.

图4 A-T-S方法和椭圆积分的误差对比
Fig.4 Comparison of the error about A-T-S model and elliptical method

图5 末端受力的柔顺杆变形能分布情况
Fig.5 Deformation energy’s distribution of the compliantlink with tip load

4 结 论

本文将链式算法和t-s模型相结合，提出了A-T-S方法，为柔顺杆的大变形分析提供了一种新的思路。该方法不仅可以计算大变形柔顺杆的末端位移和受力，还可以对柔顺杆受力后的变形情况、应变能的分布情况进行表示。它对杆末端位置、转角和受力计算的误差随着杆长分段数的增大而逐渐变小，在实际应用中可根据问题的精度要求适当选择分段数，进而达到速度和精度的平衡。由于通过此方法可以得到每一个小段所受拉力的情况，进而可以通过引入胡克定律，得到柔顺杆受力后的轴向拉伸变形，使得柔顺杆的力学分析更加精确，从而更适于实际应用。

参考文献：

[1] HAI-JUN SU.A load independent Pseudo-rigid-body 3R model for determining large deflection of beams in compliant mechanisms[C]// Information in Engineering Conference, USA,New York, 2008.

[2] HOWELL L L.Compliant mechanisms[M].New York：John Wiley & Sons，2001.

[3] HOWELL L L， MIDHA A.Parametric deflection approximations for end loaded large deflection beams in compliant mechanisms[J].Transaction of the ASME，Journal of Mechanical Design，1995，117(3)：156-165.

[4] MIDHA A，HOWELL L L.Evaluation of equivalent spring stiffness for use in a pseudo-rigid-body model of large deflection compliant mechanisms [J].ASME Transactions，Journal of Mechanical Design, 1996，118(1)：126-131.

[5] MIDHA A，HOWELL L L.A method for the design of compliant mechanism with small-length flexural pivots，ASME Transactions [J].Journal of Mechanical Design，1994，116 (1)：280-289.

[6] SU Haijun.A pseudo-rigid-body 3R model for determining large deflection of cantilever beams subject to tip loads[J].Journal of Mechanisms and Robotics，2009(1)：021008-1-9.

[7] 冯忠磊，余跃庆，王雯静.模拟柔顺机构中柔顺杆件末端特征的 2R 伪刚体模型[J].机械工程学报，2011，47(1)：36-42.

[8] HER A I, MIDHA A.Compliance Number Concept for Compliant Mechanisms and Type Synthesis[J].Transactions of the ASME.1987, 109: 348-355

[9] MIDHA A, NORTON T W, HOWELL L L.On the Nomenclature, Classification, and Abstractions of Compliant Mechanisms[J].ASME Journal of Mechanical Design.1994,116 (l):270-279

[10] 王英慧，王希云.一种求解二次模型信赖域子问题的 Adams 方法[J].太原科技大学学报，2016，37(1)：72-76.

[11] 王英慧，王希云.一种求解二次模型信赖域子问题的 Admas4 隐式算法[J].太原科技大学学报，2016，37(5)：406-411.

[12] KOTA S.Synthesis of Planar, Compliant Four-Bar Mechanisms for Compliant-Segment Motion Generation[J].Journal of Mechanical Design.2001,123：535-541.