全局检验与事后检验之间的联系：ANOVA 方差分析中F 检验结果的一项调查

Tian CHEN, Manfei XU, Jus ti n TU, Hongyue WANG, Xiaohui NIU

1.背景

组间比较是大多数生物医学和社会心理学研究中常见的问题。 在许多研究中，有两个以上的组，在这种情况下，两个（独立）组的 t 检验不再适用，必须使用比较两个以上组的模型，例如方差分析ANOVA模型[1]。 比较两个以上的组时，我们采用分层分析的方法。在这种方法下，首先进行全局检验，检验的零假设为各组之间无显著性，即所有组具有相同的均值。如果这个检验没有统计学意义，那么在数据中没有证据表明可以拒绝零假设，然后结论可以认为没有证据表明组间有差异。否则，执行事后检验以找出差异来源。

在事后检验过程中，我们对各组进行两两比较，并找到有显著差异的所有组别。这种分层分析方法的前提是，如果全局检验是有显著性的，那么至少存在两个组之间是有显著差异的，反之亦然。

分层分析方法在基础和高级统计课程中均有教授，并且内置于许多流行的统计软件包中。例如，当执行方差分析（ANOVA）模型来比较多个组时，全局检验由F统计进行[1]。 对于事后检验，可以使用一些特殊的程序，如 Tukey’s 和 Scheffe’s 检验[1]。执行事后检验需要进行特殊的统计检验，因为在执行多重检验以识别具有不同均值的组别时，出现 I 类错误的可能性会增加。Tukey’s，Scheffe’s 和其他事后检验都进行了这种多重比较的调整，以确保多重检验中具有正确的 I 类错误概率。

然而，在实践中，当全局检验是有显著性时，似乎常常没有任何事后检验是有统计学意义的。反过来也是如此; 虽然一些事后检验是有显著性的，但全局检验差异并不显著。据我们所知，目前并没有一种普遍接受的方法来处理这种情况。在本次研究中，我们研究了这种分层分析方法，并且使用模拟的数据看到它的分析效果。我们想知道一个有意义的全局检验是否能保证至少一次事后检验有意义，反之亦然。尽管比较多个组的统计学问题与所有的统计模型相关，但我们本次只专注于相对简单的方差分析（ANOVA）模型，并从简要概述这种比较两个以上组别的普遍分析模型开始。

2.单因素方差分析（ANOVA）

2.1 统计模型

方差分析（ANOVA）模型被广泛用于比较多个组的研究中。 该模型将比较两个（独立）组的 t 检验扩展至两个以上组别之间的比较[1]。

考虑一个感兴趣的连续性结果变量 Y，并让I表示组数。 我们对于比较 I 组间 Y 的（总体）均值感兴趣。经典的方差分析（ANOVA）模型具有如下形式：

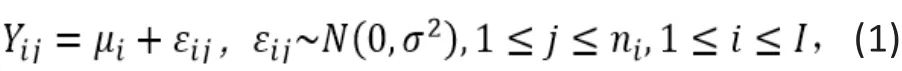
其中Yij是第 i 组内第j个样本的结果，μi= E(Yij)是第 i 组的（总体）均值，εij是误差项，表示均值为μ和方差为σ2的正态分布，ni是第 i 组的样本量。

利用等式(1)中的统计模型，组间比较的主要目的可以用如下的统计假设来表示。首先，我们想知道所有的组别是否有相同的均数。在上面的方差分析模型下，这种比较的无效假设和备择假设表述如下：

对于所有的

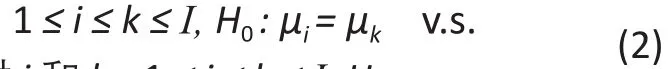
对于至少一对 i和 k，1 ≤ i ≤ k ≤ I, Hα: μi≠ μk

因此，在零假设H0下，所有组的平均值相同。如果拒绝H0支持Hα，那么至少有两组均数不同。

当进行方差分析时，首先检验公式(2)中的假设。如果这个全局检验没有被拒绝，那么可以得出结论，证据表明各组间的均数相同。否则，证据表明拒绝无效假设支持备择假设，然后进入下一步，以确定各组间均数不同。对于I个组，总共有 I(I - 1)/2 对组别需要进行检验。在事后检验阶段，我们进行I(I - 1)/2 次检验来识别具有不同均数μi的组。这个数字 I(I - 1)/2可能很大，尤其是在有大量组的情况下。因此，执行所有这些检验可能会增加I类错误的概率。使用比较两个（独立）组的流行的 t 检验此处是不适合的，必须使用专门设计的检验方法来解释由于多重检验而产生的累积 I 类错误，以确保 I 类错误概率正确。接下来我们回顾一下全局检验和一些事后检验，这些检验稍后会在我们的模拟研究中使用。

2.2 组间无差异的全局 F 检验

在方差分析中同时比较所有组间均数的全局检验是F检验。 F检验由所谓的ANOVA表中的变量定义。要建立这个表格，我们需定义以下变量：

其中N是总样本大小，=1Aj表示所有Aj的总和，=1=1Aij表示所有不同i和j的组合Aij之和，即，

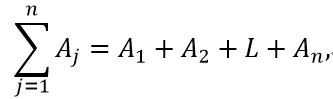
方差分析表由下表定义：

?

在上面的ANOVA表中，SS(R)称为回归平方和，SS(E)称为误差平方和，SS(Total)称为总平方和，MS(R)称为回归平方和均值，SS(E)被称为误差平方和均值。这些平方和表征(1)当忽略组内均值差异(SS(Total)) 和(2)考虑这些差异(SS(R))后的所有组间变异性。 例如，可以证明

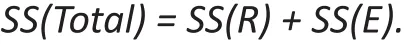
因此，如果各组均数能解释大部分组间差异的变异，则SS(R)将接近SS(TOTAL)，SS(E)则较小，在这种情况下，组间均数可能不同。 否则，SS(R)较小，SS(E)较接近SS(TOTAL)，在这种情况下，组间均数不太可能不同。使用组数对SS(R)和使用总样本大小对SS(E)进行标化，可以使用均方MS(R)和MS(E)来量化SS(R) 和SS(E)的相对差异，来帮助辨别哪组均数不同。

在零假设H0下，比值，或者说F统计量，，服从以下F-检验：

其中FI-1,N-1表示服从自由度为 I - 1（分子）和自由度为 N - I（分母）的F分布。 如前所述，相对于MS(E)的更大的MS(R)表示证据不支持零假设，反之亦然。这与 F 统计量的值较大，表示零假设被拒的事实一致，反之亦然。

2.3 事后组间比较的检验

如果F检验拒绝零假设（无组间差异），则进入下一步检验，以识别具有不同均值的组别。 通过保证I类错误概率，可以使用多个专门的程序来执行这种事后检验。 例如，如果所有组的样本大小相同，即对于所有 1 ≤ i ≤ I，ni= n，我们可以使用图基（Tukey）检验。首先对各样本组的平均值进行排序，然后根据下面的标准，利用样本均数检验两组（总体）均数是否相同，即μi= μK：

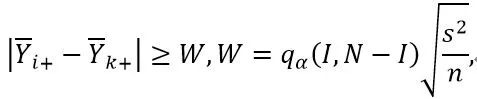
其中 S2= MS(E)，qα(I,N - I)是比较 I 组的 studentized range统计量的上临界值，N是常用的样本量大小。

2.4 模拟研究

当应用方差分析比较多个组时，我们首先执行全局F检验，如果全局检验是显著的，则进行事后两两组间比较。否则，我们停止检验并得出结论：没有证据表明可以拒绝组间无差异的零假设。该方法隐含的假设是，有意义的全局检验意味着至少有一对组间比较有统计学意义，反之亦然。如果这个假设不成立，这个方法将会(1)产生假阳性（显著的全局检验，但无显著的组间成对检验）或(2)假阴性结果（没有显著的全局检验，但至少有一个显著的事后检验）。在第一种情况下，很难在逻辑上调和这些差异并报告结果，而第二种情况也会导致错失找到组间差异的机会。在本节中，我们使用模拟数据来检验这种分层分析方法所依据的假设。

为了简洁并且不失一般性，我们考虑有四个组并且假定各组样本大小均为 n。那么，该模拟研究的ANOVA模型为：

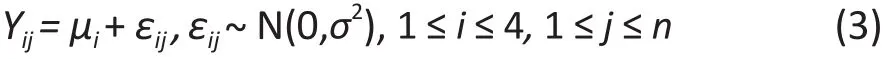
我们假设前三组具有相同的均值，即μ1= μ2=μ3，它与第四组平均值相差 d，即 μ4= μ + d，其中d>0。 对于模拟研究，我们在所有模拟中假定μ = 1 和σ2= 1 ，但是改变组样本大小 n 和 I 类错误概率α，以查看当这些参数变化时分层分析过程如何变化。

使用分层分析方法比较各组，我们首先检验零假设为四个组无均值差异的情况：

Hα:对于某些 i和 k，μi≠ μk, 1 ≤ i < k ≤ 4

如果上述零假设被拒绝，那么我们继续执行四个组的成对比较以识别彼此显著不同的组，即，

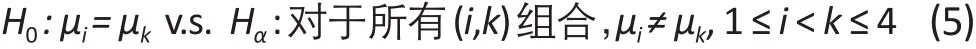
在模拟研究假设中，共进行次事后检验。

为了查看分层分析对模拟数据的分析效果如何，我们使用蒙特卡罗重复并将蒙特卡罗样本大小设置为M = 1,000。因此，对于给定的各组样本大小n，我们根据公式(3)中的ANOVA模型模拟数据Yij，然后执行F检验以检验公式(4)中各组无均差的零假设。如果F检验是有统计学意义的，我们通过在公式(5)中执行6个成对组间比较来进行事后检验过程。

表1中显示的是，当蒙特卡罗重复M = 1,000时，作为样本大小 n、差值 d 和 I 类错误概率 α 的函数，“F”下显示的是F检验对于检验无组间均数差异的零假设有显著性的次数百分比，“Tukey”下显示的是至少一个事后Tukey检验是有显著性的次数的百分比。这个百分比实际上是效能或经验效能的一个估计值，表示当零假设为假时拒绝相应的零假设的能力。由于效能随着样本大小以及均值之间的差异而增加，因此当α= 0.5和α = 0.001时，样本量n从20增加到40，并且组间均值的差值 d 从0.5增加到1，百分比增加。而且，正如预期的那样，随着α从α = 0.05降低到α = 0.001，百分比变小。

比较多个组别的目的是找出具有不同均值的组别。分层分析方法旨在通过首先执行“筛选”检验来查看是否有必要进一步深入研究，详细比较各个组别。从这个意义上说，我们可以使用由以下定义的“假阳性”（FP）和“假阴性”（FN）率表征分层分析方法的效果：

FP = Pr（事后检测没有显著性| F检验有显著性），

FN = Pr（事后检测有显著性| F检验没有显著性），

其中Pr（B|A）表示给定事件A发生事件B的概率。因此，FP是在给定F检验有显著性的情况下没有任何事后检验有显著性的概率，而FN是给定F检验无显著性而至少一个事后检验有显著性的概率。在FP的情况下，我们会得到一个错误警告，而在FN的情况下，我们错过了找到组间差异的机会。

表1中“FP”下所示的是FP的估计值，即F检验有显著性时事后检验无显著性的百分比。有趣的是，当α从α = 0.05变为α = 0.001时，FP大大增加。例如，对于n = 20和d = 0.5，当α = 0.05时，FP约为10%，但当α = 0.001时，FP增加到接近20%。换句话说，当α = 0.05时，我们有大约10%的概率得到一个错误警告，但当α= 0.001时，我们得到错误警告的概率近20%。

表1中“FN”下所示的是FN的估计值，即F检验无显著性时事后检验有显著性的百分比。与FP情况类似，FN也随着α的变化而变化。但是，与FP不同，当α从α = 0.05变为α = 0.001时，FN降低。另外，与FP相比，FN更小。例如，对于n = 20和d = 0.5，当α = 0.05时，FN约为4%，当α = 0.001时，FN小于1%。换句话说，当α = 0.05时，我们有大约4%的概率得到一个错误警告，但当α = 0.001时，我们得到错误警告的概率小于1%。

3.讨论

在本文中，我们使用模拟数据调查了全局检验的性能。分层分析方法是比较多个（多于两个）组的一种广泛使用的方法[1]。全局检验旨在没有组间差异的情况下通过减少不必要的事后检验来保证 I 类错误概率。然而，我们的模拟研究表明，分层分析方法不能保证一直有效。全局检验和事后检验并不总是一致的。由于我们比较多个组的目的是找到具有不同均值的组，所以如果没有任何事后检验是有显著性的，则有显著性的全局检验会给出错误警告。但是，最重要的是，如果全局检验无显著性，我们也可能错过检验组间差异的机会，因为在这种情况下，部分或全部事后检验可能仍然有显著性。

虽然本文中我们聚焦经典ANOVA模型，但同样的考量和结论也适用于比较多个组的比较复杂的模型，如纵向数据模型[2]。因为对于大多数模型而言，针对多重检验调整了显著水平的事后检验并没有像方差分析的情况那样具有与全局检验完全相同的 I 类错误概率，因此评估分层分析方法的效果将更加困难。例如，Bonferroni修正通常是比较保守的。

根据我们的研究结果，无论全局检验的显著性结果如何，似乎有必要总是进行组间比较，并基于这种组间比较进行结果的报告。

参考文献

1.Kutner MH, Nachtsheim CJ, Neter J, Li W.Applied Linear Models, 5thed.New York: McGraw-Hill/Irwin; 2005

2.Tang W, He H, Tu XM.Applied Categorical and Count Data Analysis.FL: Chapman & Hall/CRC; 2012