经历关键步骤理解关键意义
——《用字母表示数》教学实践与反思
贾春波
【教学内容】
人教版五年级。
【教学实践与反思】
一、不确定(未知)情况可用字母表示
1.表征对象从确定到不确定(如下图)。

出示问题情境,学生尝试表达,然后依次呈现出一些典型表征方式。
师:(提出关键问题)老师看了同学们的作业后,发现前两幅图大家表示一致:3和5,而第三幅存钱罐的表示却不同,这是为什么?
生:前面的硬币个数确定,是3和5;存钱罐里的是未知、不确定的。
师:看来同学们都认为前两幅图的硬币个数是确定的,可用数表示;而存钱罐的硬币个数无法确定,是未知的,所以大家的表示方法就各不相同。
2.聚焦未知表征的对比。
师:(提出关键问题)存钱罐里用“8”“未知”“x”这三种方法,你欣赏哪一种,为什么?
生:我喜欢第二种,“8”只表示了一种,而用文字写的意思很明白。
生:我选第三种,“8”表示一种,但还有很多可能,用文字写较麻烦,字母较为简单。
生:我也选第三种,“8”是确定的,而存钱罐里的钱是未知的、不确定的,字母可以表示多种情况,又简洁。
师:通过讨论可知,确定的情况用数表示,不确定的情况可用字母表示。
【反思:用字母表示未知量,人教版教材没这个环节,之所以安排,是因为历史发生原理指出,学生应经历“记数→未知→一类”这三个步骤。更为重要的是,从记数到未知的过渡,其关键是表示的对象发生变化,即从“确定”到“不确定”,随之表示的意义也发生变化。确定情况用数来表示,学生已积累较为丰富的经验,但对“不确定情况怎么表示?为什么用字母表示比较好?”等问题知之甚少。实践中用两个对比,让学生思辨其内在原理。对比一:通过圈内确定的硬币数与存钱罐内不确定的硬币数对比。不确定情况下,再用“具体的数”表示,就有其不足之处,即具体数只能表示出一种具体情况,所以要选用其他的方法;对比二:“未知表征”形式的对比。通过比较发现,具体数、文字、字母三种典型的表征方式,每一种都有其优缺点,其中字母因为简洁、又具有不确定性,用来表示未知、不确定情况最为合理。】
二、字母表示一个集合中的任意情况
1.具体与抽象的对比。
师:刚才大家认为,存钱罐里的1元硬币数是未知的、多种情况的,所以用字母来表示,x可以是0个,也能是1个、2个……,最多是200个。(指这个存钱罐最多放的1元硬币数)那用1与x表示存钱罐里的硬币数有什么不同呢?
生:1只能表示一种情况,x能表示存钱罐里所有可能硬币数中的任意一种情况,如0~200中的任意一个数。
2.特殊与一般的对比(如下图)。
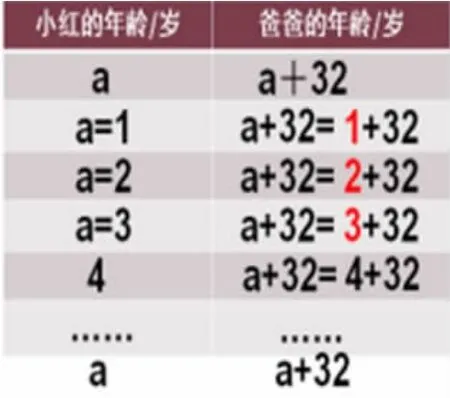
师:4与a都可表示小红的年龄,4与a有什么不同?
生:4只表示一年的年龄,a表示任何一年的年龄,也就是从出生到死亡的任何一个年龄。
师:4+32与 a+32 都可表示爸爸的年龄,这两个又有什么区别?
生:4+32只表示爸爸36岁一年的年龄,a+32则可以表示32岁以上的任何一年年龄。
【反思:从字母表示数意义的“未知量”阶段过渡到“一类量”阶段,其主要的问题是表示“对象”的意义发生“质变”,即从特定量(特殊)到变量(一般)。数只能表示一个特定的情况,字母不仅能表示特定一种情况,还能表示一个集合中任意一个值的量。这是两者的本质区别,也是字母表示数的优势所在,即能一般化的表示一类量。它是从算术思维过渡到代数思维“质”的飞跃的重要标志。在教学中,让学生经历两次“具体数”与“字母”的对比思辨,从而理解字母是表示一个集合中的任意一个数。
实践中,学生对字母表示未知量“x”意义的理解处在不同的水平层次。经过对比、思辨、交流等数学活动,促使学生对字母表示数的意义理解从低水平层次向高水平层次转变,较为深刻的理解字母表示变量的意义,也进一步体会到字母表示数的优越性。也为用字母式表示具体情境中的数量关系(变量),及辩论“4+32”与“a+32”的不同,铺垫了理解的基础。】
三、字母式既表示关系又表示数
1.重构“=”意义,感悟“式”表示数(如下图)。
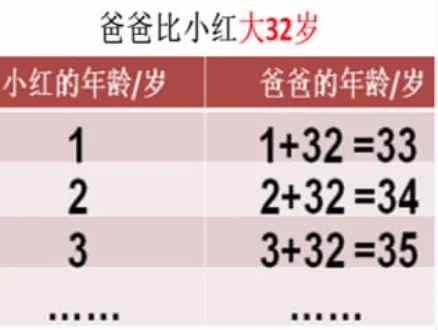
师:这些算式中“=”表示的是什么意思?
生:小红年龄+32等于爸爸的年龄。
师:左边的1+32与右边爸爸的年龄33是相等的。那“1+32”算式可以表示爸爸的岁数吗?
生:可以表示,因为左右相等。
师:那你喜欢用1+32还是喜欢用33来表示爸爸的年龄呢?
生:我喜欢33,因为它很清晰。
生:1+32,能看出爸爸的年龄,还知道比小红大32。
2.迁移比较,感悟“字母式”表示数(如下图)。

师:看数学信息,知道了什么?
生:贾老师比小红大28岁。
师:你是怎么知道的?
生:a+28,是用小红年龄a加28得到的。
师:这么说,a+28不仅表示贾老师的年龄,还表示贾老师与小红年龄间的大小关系。那刚才的a+32又表示了什么呢?
生:a+32不仅表示了爸爸的年龄,还可看出爸爸比小红大32岁这个关系。
师:根据刚才的经验,想一想“(a+32)+30”会是谁的年龄?
生:爷爷岁数,a+32是爸爸年龄,爷爷比爸爸还要大30岁。
生:只要比爸爸(a+32)大 30岁的人都有可能。
师:(a+32)+30表示了什么意思?
生:表示比爸爸大30岁的岁数,又表示比爸爸大30岁的关系。
【反思:能理解字母式既能表示关系(过程),又能表示对象(结果)是理解字母表示一类量意义的重要的标志。在代数中,如字母式a+32,既表示a与32相加这一个过程操作,又表示为对象、结构,即a+32的结果就是a+32。然而正是这种既表示过程又表示对象的“二重性”特征,给学生造成了主要的理解障碍。它之所以难,不仅仅是因为它本身具有的抽象性,还在于对它的建构,要抵制已有知识经验的强烈负迁移。因为“式”(如 2+32)算术中,具有操作性的、表示过程的,目的是求结果,学生潜意识中要把2+32计算为34;而在代数运算中是结构性的,是形式变换,关注结构,注重关系,此时的“式”除了体现过程外,更多是关系结构的形式化。
为突破,先重构“=”意义,铺垫理解基础。Booth提出“如果学生不能理解两个集合(假定分别含有5个和8个)物件的总数可以写成5+8,那么要他们理解a+b表示了两个集合(分别含有a个和b个)物件的总数就更不可能了。”然要改造学生已有的经验,要结合“=”意义重构一起进行,因为“=”在算术中,代表运算得到结果,是具有方向性、程序性的。而在代数中,“=”代表一种等价关系,因此“=”左右两边需有同样的大小,没有方向性,具有结构性。先认识到33与1+32是等价的,都能表示爸爸的年龄,且1+32还能看出与小红的关系,有了这样的理解基础,迁移到a+32表示爸爸的年龄就简单多了。
为突破,再类比推理,思辨说理中加深理解。从a+28中能得到什么信息?在解决中,学生需要拿“a+28”与“a”进行比较。比较时,先是把a+28看成一个数,与a比较后得出大28岁,则把a+28理解成了一种关系。然后自然类比到对“a+32”和“(a+32)+30”的理解,在思辨、说理中加深了对字母式既表示关系又表示数的理解与建构。】

