小学数学深度学习的三个维度

李雯 林琦

随着谷歌公司开发的人工智能程序“AlphaGo”相继击败人类顶尖围棋手李世石、柯洁，其背后蕴含的深度学习概念成为人们竞相研究的热点，希望通过深度学习让计算机像人类一样思考，模仿人类的学习过程。而在教育领域，相对于浅层学习的深度学习也同样备受关注。

21世纪是计算机网络的时代。相较于人类，计算机的知识储存量更大，运算速度更快，没有肉体的局限，抑或任何情绪的变化。这些优点致使如今很多职业都受到极大的冲击：制造业工人、司机、快递员等，这类简单的、固定的、重复性高的岗位都将面临被取代的风险。可见，提倡深度学习是顺应时代发展的需要。

那么，什么样的学习才称得上是深度学习？

一、深度学习的界定

20世纪70年代，马顿和萨尔约从学习方式的角度，将学习分成浅层次学习取向和深层次学习取向，提出浅层学习是指学生对材料内容的死记硬背，即“复制型”学习，深度学习则是指学生主动地理解文章内容。

90年代，比格斯将学习过程分成三个层次：1.运用，简单熟练地运用所学知识。2.内化，对所学知识颇感兴趣，将所学材料和已有认知结构建立起有意义的联结。3.成就，学生渴望成功，能够合理地安排时间，有效地完成任务。在这里，“运用”对应浅层学习，“内化”与“成就”对应深度学习。美国国家研究委员会（NRC）则认为深度学习是学习迁移的过程，将在一种情境中学习到的知识运用在另一情境中，即知道如何迁移，为什么迁移，以及何时迁移知识去解决新问题。

美国“关于深度学习的调查研究：机遇与成果（简称SDL）”的项目从学习结果的角度，将深度学习界定为学生在21世纪工作与生活所必需的，且通向高等教育的高阶知识与技能。从三个维度（认知领域、人际领域和自我领域）区分出六种能力：掌握核心学科知识、具有批判性思维和解决复杂问题能力、有效沟通与交流、团队协作、学会学习以及具有学术信念。

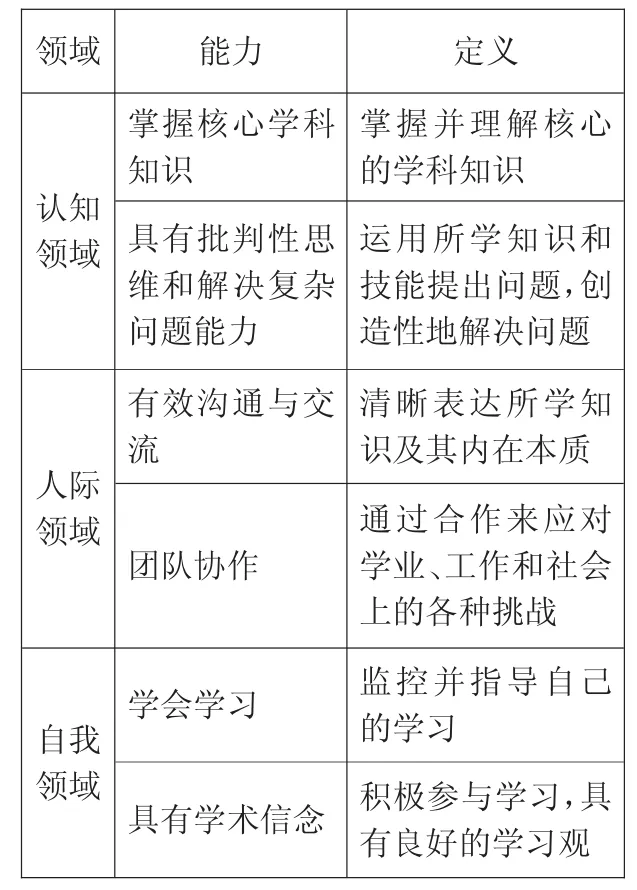
借鉴上述定义，我们界定深度学习为：在掌握核心知识和运用所学解决复杂问题的同时，以批判性的眼光审视学习内容与过程，具有较高的学习参与度，并获得高阶思维与技能的学习。

二、小学数学的深度学习

当今深度学习的研究多集中于中学和高等教育阶段，但它对于小学阶段的数学学习来说也有一定的启示。虽然儿童尚未形成系统的数学知识体系，但这并不能说明小学数学就是浅层学习，没有进行深度学习的必要。下面从学习方式、学习过程和学习结果三个方面对小学数学的深度学习进行讨论。

1.学习方式的深度。

首先，深度学习强调有意义学习，反对“复制型”的死记硬背。比如在学习负数时，考虑到小学生已经有了购物的生活经验，那么就可以从“正盈负亏”的角度来理解正负数——正数表示盈利，负数表示亏本。在这里，我们赋予负数“亏本”的意义，而不只是记忆有减号的数就是负数。

其次，能够对所学知识做出批判性思考。第一，抓住问题的关键，在扑朔迷离的各种现象中抓主要矛盾，体现数学的本质。第二，具有质疑的意识和能力，经常思考别人为什么会提出这样的方法，善于提出问题，寻求对这些问题的解答。第三，在思考问题的方向上具有发散性和原创性，大胆进行方法和策略的创新，具有较强的创新意识和创新思维能力。比如，教师在讲到“一组对边平行的四边形是梯形”时，学生能够提出质疑：“平行四边形的两组对边都互相平行，那么平行四边形也是梯形吗？”由此引出梯形的严谨定义“只有一组对边平行的四边形是梯形”。在学习梯形面积时，学生能够通过多种割补法，转化成三角形、长方形、平行四边形等不同图形来求得梯形面积。

2.学习过程的深度。

根据NRC的定义，深度学习体现在学习迁移上，这一点和国内学者张浩等人的研究不谋而合。而在小学数学学习过程中，学习迁移从低到高可以分为四个层次：

第一，从一道题到另一道题的迁移，从而解决一个类型的题目。要求学生能够辨别出题目中具有相同的数学原理，即掌握“问题原理”。只有这样，在遇到新问题时，才能将其纳入某个问题原理中处理。例如，在解决不规则图形的面积问题时，其问题原理就是通过分割或填补成规则的图形，再由规则图形的面积得到不规则图形的面积。

第二，从一个数学领域迁移到另一个数学领域，形成系统的知识网络。孤立地学习某一特定部分的知识，犹如“管中窥豹”，难以全面地认识数学，甚至以为数学的学习就是数的学习或是图形的学习，阻碍学生之后灵活地运用数学。这就要求学生对数学的各个部分都有清晰的认识和理解，是借助深层次学习方式来达成的。此外，学生要具备主动建立知识间联系的意识，能够从一个领域联想到另一个领域，如下题。

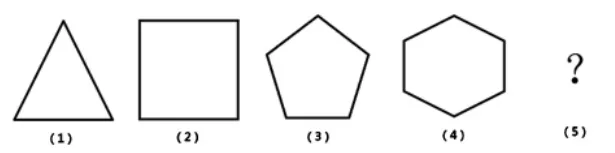
几何与代数的联系

表面上是图形题，实质考察的却是代数内容。学生要从图形问题联想到代数内容，抽象出代数知识，继而借助数的思想方法解决该问题。

第三，数学与其他学科之间的迁移。不仅物理、化学等理科蕴含着丰富的数学知识，语文、地理等学科同样如此。比如，地图上的比例尺就是数学中比例关系的实际应用。标准中国地图上的比例尺是1∶18000000，意味着地图上的1厘米等同于现实生活中的180千米。学生只有全方位地掌握各门学科的知识，才能建立彼此的联系，更深层次地理解和运用数学与其他学科。

最高层次的迁移是在不同情境中的数学迁移，主要指生活情境和学校情境间的转化。一方面，学生能够将学校所学的数学知识运用到现实生活中。另一方面，也能从日常生活中抽象出数学知识，丰富数学的理解。

四个层次，每个层次都是在前一层次的基础上形成的。不同情境下的灵活转化，是在达成前三种层次的基础上满足的。

3.学习结果的深度。

我们根据SDL项目的框架，并结合《义务教育阶段数学课程标准（2011年）》，从认知、人际和自我三大领域对小学数学所应当发展的能力进行说明。

在认知领域，学生应在掌握并理解代数知识、几何知识和统计知识的基础上，加以批判性的思考，即学习方式上的深度学习，在此就不再赘述。

在人际领域，学生能够把自己理解的知识及其本质，以书面或口头的形式呈现出来，与同学进行有效的沟通。既能倾听他人的意见，虚心接受，也能为他人提供建设性的反馈。小学生课堂气氛活跃，不乏沟通交流，但还不能很清晰地表达自己的想法。因此，教师应当鼓励学生多多表达，通过提问、辅之以动作，来帮助学生组织语言。而数学教师则更要关注学生用数学语言、数学符号来表达和交流。

学生在这基础上进行合作学习，获得团队协作的能力。但要避免过于形式化，不能为了合作而合作。合作学习的形式虽然能很好地激起学生的学习兴趣，但也容易让学生只专注于形式，却忽视思考，重“合作”而轻“学习”。因此，在合作学习前要让学生明确学习的目标，过程中要进行适当的指导，做到“形散而神不散”。

在自我领域，学生要学会学习，即监控并调整自己的学习，其关键在于反思，这也是贯穿于学习过程始终的。学习前，通过反思来了解自己已有的知识经验和能力水平，确立学习目标，制定合理的学习计划。学习中，通过自我提问、师生评价、档案袋等方法，不断调整知识的获得、转化和运用来提高效率。最后，总结经验教训，正确地评估解决问题的方法，思考更优化的策略。

在小学阶段，教师还应帮助学生逐步形成正确的学习观和数学观。其一，数学学习不是任务，是提高自身的机会。数学学习不是枯燥的，而是富有趣味的。当学生解决一道数学难题时，他们获得了成就感；当他们运用数学知识解决实际问题时，能够体会到数学学习的价值所在。其二，相信自己的能力，也就是具有较高的自我效能感。只有对自己数学学习能力充满信心之后，学生才更愿意投入到学习中。其三，形成正确的归因观，相信付出就有回报。当学生将失败归因于缺乏努力时，即使遇到失败和挫折也能很快投入到新的学习中。

我们对深度学习加以定义，并从学习方式、学习过程和学习结果三个角度来研究小学数学的深度学习。在学习方式上，倡导有意义学习和批判性学习；学习过程强调深层次的学习迁移：掌握“问题原理”，形成系统的知识框架，建立多学科之间的联系以及在不同情境的灵活转化；最后，根据SDL项目的框架阐述小学数学中深度学习的学习结果。

深度学习的三个维度并非是完全独立的，而是相互联系的。学习结果要求进行深层次的学习方式，是经历过深度学习的过程才发展的能力。而从不同的角度界定深度学习，有利于我们理解深度学习，进而对小学数学学习提出指导性意见。