《因数和倍数》教学设计

杨传冈（特级教师）

【教学内容】

苏教版五年级下册第30、31页。

【课前思考】

因数和倍数是数论的基础性概念，在小学阶段有过一些变革和调整，如苏教版教科书有一段时间曾前移至四年级，现后移编排在五年级下学期，充分尊重了学生的理解能力和已有知识结构。教过这部分内容的教师或许都有这样的感受：学习内容较为抽象，知识点零碎，课堂容量较大，学生很难迅速理解和熟练掌握。

《因数和倍数》一课的整体设想是：关注概念生成，让学生感悟知识来源；关注范例教学，让学生发现概念形成过程；关注思想渗透，让学生领悟概念本质；关注开放练习，让学生融会贯通知识体系；关注文化拓展，让学生明晰知识效用。

具体来说，深入领会编者意图，以教科书为蓝本，充分遵循知识的产生和形成过程，通过学生预学交流，了解评判学生的认知起点，重点选择学疑之处、学难之处；依托活动导学，通过生生互学、师生共学，着力从学生学困之处寻找突破口，帮助学生调取已有的知识经验，强化概念的理解和建构。全课围绕因数和倍数的找法及特征，以数学思考为主线，以数学活动为脚手架，引导学生想思、会思、能思、爱思，思成。从学生的认知现实出发，既不拔高也不降低，注重教学目标的多元化、学习方式的多样化、学习元素的开放化、学习评价的及时化，以活动模块分散难点，强化因数倍数相互依存的本质属性，以开放的视角直面知识体系建构，突破因数和倍数概念理解的难点。另外，在学习价值的目标取向上不局限于学生获得一般的数学知识和形成一定的技能。而是精心选择学习素材，在供给学生鲜活学习素材之前铺垫包袱，揭示时带给学生更多的惊喜，让学生在亲身经历中感悟、领略数论基础的内在规律及文化魅力，激发学习数学的兴趣，激活学好数学的信心，在学习过程中体悟数学基本思想，积累基本的数学活动经验，提升解决问题的能力。

【教学设计】

一、课前活动，直面难点

师：同学们喜欢玩脑筋急转弯吗？有三个人，其中有两个爸爸，两个儿子，你能说出他们之间的身份关系吗？

（引导学生说清三个人的关系，重点强调：谁是谁的爸爸，谁是谁的儿子）

【设计意图：课前活动设计的主要目的有两个：一是通过有趣的脑筋急转弯活跃现场气氛，拉近师生之间的距离，打消学生的畏惧心理；二是为学生顺利理解因数和倍数的相互依存关系埋下伏笔。】

二、预习反馈，了解学情

师：本节课我们要学习的内容是《因数和倍数》，课前老师布置了预习任务。通过预习，你有哪些收获？还有哪些困惑？

（梳理：因数和倍数不是一种数，而是数与数之间的关系；怎样找一个数的因数；怎样找一个数的倍数；因数和倍数个数的特点……）

师：相信通过今天的共同探索、交流学习，你一定能破除困惑，建立正确的认识。

【设计意图：在有限的课堂学习时间内，如何才能紧扣学生思维的脉搏同频共振？如何才能和学生一起经历思维的起伏跌宕？这些都离不开教师恰如其分地了解学生的学习起点，并据此确定学习流程，调适学习进度、时间分配、学习形式等，从而有效提升学习效益。正所谓知己知彼方能百战不殆。】

三、拼图引入，建立概念

1.思维拼图。

师：让我们一起先来做个热身运动吧。你能快速说出由12个边长是1厘米的正方形可以拼成怎样的长方形吗？想到几种可以说几种。

2.统一拼法。

师：我们一起来整理一下：长 12，宽 1；长 1，宽 12（课件呈现具体拼法），这是两种拼法吗？（不是）它们旋转后是一样的（课件呈现旋转过程），数学上认为是一种拼法。写成算式为12×1=12。还有什么不同拼法？怎样用算式表示？

（根据学生补充，课件呈现另两种拼法及算式）

3.感知概念。

（1）概念揭示。

刚才三种不同的摆法，相应地可以用三道不同的乘法算式表示。以3×4=12为例，数学上说3是12的因数，4也是12的因数；12是3的倍数，12也是4的倍数。（课件演示）

明确：研究因数与倍数时，所说的数一般指——（课件出示：非0自然数）

（2）强化练习。

这两道算式 2×6=12，1×12=12，你能也试着说一说谁是谁的因数，谁是谁的倍数吗？

4.内化概念。

下面每个方框里的两个数，哪个数是哪个数的因数？哪个数是哪个数的倍数？

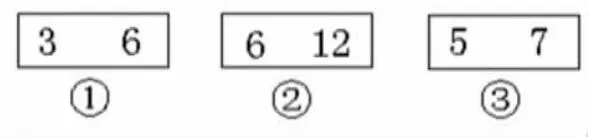
（教师捕捉学生发言中的表述漏洞，引导学生明晰因数、倍数是两个数之间的关系，这两个数都是非0自然数）

5.12的因数。

师：除了这三道算式，你还能找到两个自然数相乘的积是12吗？（课件出示 4×3=12，2×6=12，1×12=12）

师：不能了，所以12的因数有？

教师示范、指导一个数因数的写法，如 12 的因数有：1，2，3，4，6，12。（一对一对地找，按照从小到大的顺序排列，每相邻两个数之间用逗号隔开，注意保持合适的间距）

小结：在非0自然数范围内，因数的背后总能找到与之相对应的乘法算式或除法算式。

四、活动探索，研究因数

1.找36的因数。

活动要求：

1.想一想：你打算用什么方法找全36的因数？

2.议一议：怎样找才能做到不重复、不遗漏？

3.写一写：把找到的36的因数按顺序记录下来。

4.说一说：把自己找36的因数的过程在小组里说一说。

2.交流建构。

（展示学生活动单，师生活动交流学习成果）

寻找方法：有序思考，根据乘法或除法算式一对一对寻找。

在临床思维能力、操作能力、团队协作能力方面，SBMEPBL组的赞成比例明显高于PBL组（P＜0.05）；在提高自学能力、学习兴趣方面，SBME-PBL组和PBL组两组的赞成比例差异无统计学意义（P＞0.05）。详见表3。

寻找原则：不重复，不遗漏。

方法保障：有序思考。

特例指导：处理类似6×6=36，只算一个6为36的因数。

书写指导：写36的因数时，可以先在草稿上试着写好，再按照从小到大的顺序誊写；如果能控制数与数之间的距离，可以直接书写，每相邻两个数之间用逗号隔开。

集合图表示：

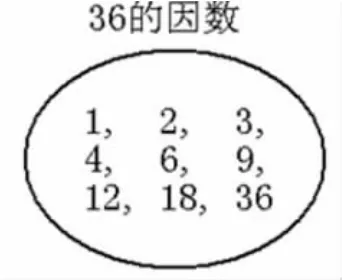
数形结合表示：

师：按照一对一对的方法，从小到大寻找一个数的因数，到什么时候就可以结束呢？让我们一起来看。（屏幕出示：在数轴图上从 1，36；2，18；3，12；4，9；6，6 逐对显示，带领学生感知使用这种找法寻找因数时两个因数之间的距离越来越小，从而明确找到因数6时不再找下去）

3.及时练习。

（学生分别写出6、11的因数，并交流）

师：你是怎样找到？找全了吗？

4.探索规律。

12 的因数有：1，2，3，4，6，12。

36 的因数有：1，2，3，4，6，9，12，18，36。

6 的因数有：1，2，3，6。

11 的因数有：1，11。

（1）观察思考。

观察这些例子，独立思考这些数的因数有什么特点？如果有困难，可以小组里商量。

（2）交流发现。

（不同学习层次的学生汇报发现）

教师根据学生的发言，引导他们从一个数最小的因数、最大的因数、因数的个数等纬度展开交流、讨论，形成共识，使学生理解为什么因数个数是有限的。

（3）归纳（课件出示）：一个数的因数最小是1，最大是它本身，一个数的因数个数是有限的。

【设计意图：如果说学生借助于形的直观去认识一个数的因数，那么对于任意数的因数就需要学生通过较为抽象的乘法（或除法）算式来探寻其一般方法。借助概念形成部分的经验，学生通过合作学习顺利发现找一个数因数的一般方法后，教师再借助集合图、数轴图等数形结合的方式进一步帮助学生释疑解惑，促进学生自主建构完整的认知体系，进而通过猜想、实验、观察、验证比较等提炼总结出一个数因数的特征。】

五、活动探索，研究倍数

1.找3的倍数。

活动要求：

1.想一想：你打算用什么方法找3的倍数？

2.写一写：把找到的3的倍数按顺序记录下来。

3.议一议：3的倍数能说完、写全吗？可以用什么符号来表示？

4.说一说：把自己找3的倍数的方法在小组里说一说。

2.交流建构。

（展示学生活动单，师生交流学习成果）

寻找方法：有序思考，根据乘法或除法算式一个一个地找，3×1=3，3×2=6……以此类推，会有无数个这样的算式，所以一个数的倍数有无限个。

寻找原则：不重复，不遗漏。

方法保障：有序思考。

书写指导：写3的倍数时，可以按照从1倍开始逐一写出，一般写出5个后，就在后面添上“……”，每相邻两个数之间仍然用逗号隔开。

集合图表示：

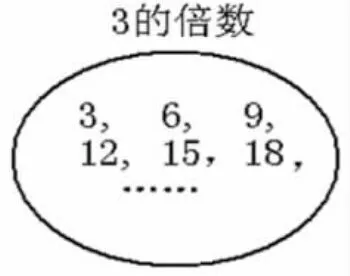
数形结合表示：

师：在数轴上能找到3的倍数所对应的点吗？这样的点有多少个？

（根据学生口答，从 3，6，9，12……逐一对应的点呈现）

3.及时练习。

（1）说出并写出2的倍数。

（2）说出并写出5的倍数。

4.探索规律

3 的倍数有：3，6，9，12，15……

2 的倍数有：2，4，6，8，10……

5 的倍数有：5，10，15，20，25……

（1）观察思考。

观察这些例子，独立思考这些数的倍数有什么特点？如果有困难，可以小组里商量。

（2）交流发现。

（不同学习层次的学生汇报发现）

教师根据学生发言，引导他们从一个数最小的倍数、最大的倍数、倍数的个数等纬度展开交流、讨论，形成共识。

（3）不完全归纳。

师：是不是任意一个非零自然数的倍数都有这样的特点呢？自己任意找一个自然数，找一找，说一说，和同桌交流一下。

（4）形成结论。

屏幕出示：一个数的倍数最小是本身，没有最大的倍数，一个数的倍数个数是无限的。

【设计意图：比起一个数的因数，学生对倍数有较为直觉的认知，他们有二年级学过一个数的几倍是多少的数学经验，教师也在引导学生用乘法（或除法）算式强化概念的本质认知。这样按从小到大的顺序探索一个数的倍数，师生在充分互动合作中经历了一个数的倍数有无限个的发现过程，并借助集合图、数轴图等方式帮助学生强化对概念的理解和掌握，使他们在猜想、实验、观察、验证、比较中提炼总结出一个数倍数的特征。】

六、全课总结，梳理脉络

通过这节课的学习，你有哪些收获？

【设计意图：总结有助于学生把所学知识初步形成脉络分明、层次清楚的结构图，帮助学生抓住知识本质，为学生内化新知奠定基础。】

七、多样练习，效度达成

1.猜猜这个数是几？（题目逐一出现，抢答）

1.一个数最小的倍数是60，这个数是多少？

2.一个数最大的因数是90，这个数是多少？

3.一个数的最小倍数和最大因数都是100，这个数是多少？

4.一个数的最小因数是1，这个数是多少？

2.猜猜谁的因数个数多？

60、90、100 这几个数，哪个数的因数最多？

生：100的因数多。（预测）

（释疑，引入60进制的缘由）

【设计意图：知识是一个网络，学习就是帮助学生建立网络。通过“猜猜这个数是几”这个游戏活动，植入开放元素，将答案不唯一的习题引入到概念教学中，在学生异口同声回答是“1”后陷入5秒左右的集体静默中，学生充分关联新学知识的相互联系发现问题答案的不唯一，沟通因数和倍数之间的内在联系，实现知识体系的自我建构和完善。第二次猜想将学生的学习热情推到制高点，他们猜想受挫后，教师适时推出60进制的缘由犹如久旱甘霖，让学生恍然大悟，又有所不甘，期待课后的深度探寻验证。这样不仅能有效激发学生的探究欲望，还能令课堂教学浑然一体，更有数学味。】