沟通内在联系完善知识结构
——《异分母分数加减法》教学设计
钱学锋(特级教师)
【教学内容】
苏教版五年级下册第80、81页。
【教学过程】
一、复习旧知,做好铺垫
师:我们已经学习了同分母分数加减法,回想一下同分母分数怎样相加减?怎样理解“分母不变,只把分子相加减”?
【设计意图:通过复习同分母分数加减法的计算法则,重点强调同分母分数相加减分母不变只把分子相加减的算理。分母不变说明分数单位相同,分子相加减就是把相同分数单位的个数相加减。引导学生把关注点放在分数单位是否相同上,为学生下一步的学习做好铺垫。】
二、创设情境,引出课题
1.出示信息,提出问题。
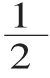
【设计意图:从学生的实际学情和教学的需要考虑,这里没有使用教材中的例题,而是以学校正在开展的实践活动为背景创设情境,把学生熟悉的日常生活情境引入教学,把知识的学习转化为解决现实生活中的问题,沟通了数学与现实生活的密切联系,使学生对数学产生亲近感,易于激发学习兴趣。同时让学生根据情境所提供的信息提出问题,可以有效培养学生的问题意识。特别是选取的数据在计算时具有典型性,在接下来的教学中各有作用。】
师:根据以上信息,你能提出什么问题?
学情预设:学生可能提出五花八门的问题,并不要求有标准答案,重点是让学生开放思考,能根据信息发现并提出问题,只要合理均给予肯定。
2.梳理问题,列出算式。
师:刚才同学们提了许多有价值的问题,梳理一下这些问题,有求和的、有求差的,老师从中选择了三个问题作为我们这节课研究的例子。
问题一:五、六年级共分得这块地的几分之几?
问题二:四、六年级共分得这块地的几分之几?
问题三:五年级比三年级多分得这块地的几分之几?
【设计意图:学生提出的问题很多,只要合理教师都要给予肯定,要体现适当的“放”,但教学中显然不可能都用,因此教师必须学会“收”。在充分肯定学生会提问的同时,要有目的地对问题进行梳理,选出本课教学最具典型性的三个问题作为例题。这样设计较好地体现出学生主体与教师主导的关系。】
师:这三个问题大家会列算式吗?
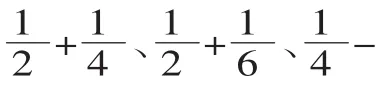
3.观察比较,揭示课题。
师:观察这些算式,与我们学过的分数加减法有什么不同?
生:分母不同。
师:分母不同的分数我们称之为异分母分数,这节课我们将以这三个算式为例来学习异分母分数的加减法。
(板书课题:异分母分数加减法)
三、探究算法,理解算理
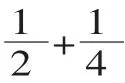
(1)小组合作。
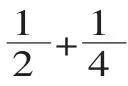
教师出示合作要求:

②想一想:可以运用已有知识解决这个问题吗?自己独立在练习纸上计算。
③在小组内交流各自的算法,可利用学具加以解释。
(学生小组讨论,教师巡视指导)
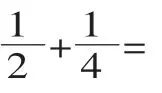
(2)交流展示。
师:刚才大家讨论的积极热烈,现在选几个小组说说你们是怎么想的?怎么算的?
学情预设:对于第一个问题“分母不同,它们能直接相加吗?请说出理由。”由于有同分母分数的学习基础和本课开始时的复习铺垫,学生很容易说出之所以不能直接相加减是由于分数单位不同。算法会出现两种:一种是先通分再相加,另一种是先转化为小数再相加。应把交流的重点放在第一种算法上。引导学生说出运用了通分、同分母分数加减法的法则、分数化小数、小数加法的法则等知识,渗透转化的思想方法,再利用学具说出通分的理由。
(3)比较异同。
师:同学们比较一下这两种算法的思路有什么相同,有什么不同?
(学生讨论后回答)
【设计意图:通过比较两种算法,使学生明确算法虽然不同,但都是转化为已有的知识解决了新问题,渗透了转化的思想方法。】
师:大家通过交流,在自己所用方法之外,都听明白另一种计算方法了吗?在了解他人的算法之后再比较一下,你们喜欢哪种算法呢?说说理由。
学情预设:有的学生通过比较可能会选择他人的算法,有的学生仍然会坚持自己的算法,只要学生言之有理,教师都给予肯定,不强求学生必须用先通分再相加的方法。
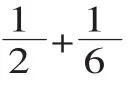
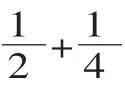
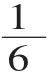
(教师巡视指导,搜集典型例子)

师:注意计算的结果能约分的要约成最简分数。
(学生说一说解题步骤)
师:为什么要先通分?
学情预设:学生的回答不一定完整,但在与教师的交流过程中,教师要明确要点:分母不同即分数单位不同,不能直接相加,必须通过通分统一分数单位再相加。
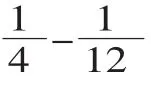
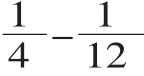
【设计意图:由于学生前面已经有了异分母分数相加的学习经验,计算这道题时学生通过迁移类推就能认识到:异分母分数相减也要先通分化成相同的分数单位,再按照同分母分数减法的法则计算。】
学生做完后,全班交流验算方法和过程,引导学生得出分数加减法的验算方法与整数加减法的相同。强调在计算时要养成自觉验算的好习惯,确保计算的正确性。
师:我们已经计算了三道异分母分数加减法的题,大家考虑过没有,在计算这类题时的关键是什么呢?(通分)结合以上的计算,同学们能试着总结出异分母分数加减法的计算方法吗?
同桌互相议一议异分母分数相减的方法,在此基础上引导学生概括出异分母分数加减法的计算方法:异分母分数相加减,先通分,然后按照同分母分数加减法进行计算。
【设计意图:在经历三个层次的计算之后,学生感受了层层递进的异分母分数加减法的计算过程,就能比较容易的总结归纳出计算方法。同时有利于培养学生的归纳、概括能力。】
师:计算异分母分数加减法的关键是什么?
(学生讨论回答)
小结:一般情况下,计算异分母分数的加减法时,先通分,转化成同分母分数的加减法,然后按同分母分数加减法的计算方法进行计算。注意在通分时,为了计算简便,应选择分母的最小公倍数做公分母,计算结果能约分的要约成最简分数,计算后要自觉验算。
四、应用知识,巩固提升
1.先计算,然后任选两题进行验算。
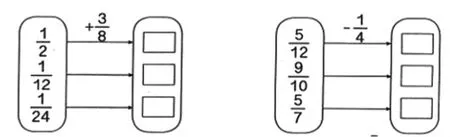
2.教材第95页练习二十四第5题。
学生填写在教材上,全班交流,引导学生重点说出错因。
3.人们在日常生活中所产生的垃圾叫做生活垃圾。
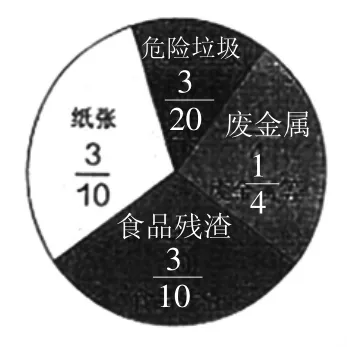
(1)纸张和废金属等是垃圾回收的主要对象,它们在生活垃圾中共占几分之几?
(2)危险垃圾多还是食品残渣多?多的占生活垃圾总量的几分之几?
五、回顾总结,完善认知
师:请同学们回忆整数加减法、小数加减法是怎样相加减的?它们与分数加减法有什么相同和不同?
(学生先独立思考,再同桌讨论)
教师在学生汇报时追问:它们是怎样相加减的?为什么强调相同数位对齐、小数点对齐、先通分?整数、小数、分数加减法之间有什么联系?
【设计意图:学到这节课,学生在小学阶段有关整数、小数、分数的四则运算都学完了,有必要沟通三者之间加减法的联系,强化四则运算加减法的算理。引导学生找出三者之间的联系,整数加减强调相同数位要对齐,小数加减强调小数点对齐,分数加减强调先通分,其本质就是“相同计数单位才能相加减”。】
【设计思路解读】
1.算理算法融合,培养学生能力。
在异分母分数加减法的教学中,要加强学生计算能力的培养。学生在计算时不仅会算,还能根据分数特点灵活选择算法。而计算能力的形成有两个前提,一是学生对算法的掌握必须建立在对算理高水平理解的基础上;二是学生必须在观察、分析、比较、交流、探究等数学活动中学习。因此,正确处理好算法与算理的关系并设计相应的数学活动尤为重要。
本课教学分三个层次有效融合算理算法。首先,学生小组合作探究,把新知转化为旧知,感悟转化思想,通过数形结合,初步理解算理。其次,设置认知冲突,学生独立思考、探究、交流,进一步掌握算法、理解算理。最后,学生由异分母相加迁移类推到如何相减,小组讨论,概括算法、深悟算理。在这三个环节中,算法算理相依并行,学生经历了由浅到深、由具体到抽象、由特殊到一般的学习过程,体现出算理算法的有效融合,有利于学生计算能力的培养。
2.沟通内在联系,完善知识建构。
数学学习是基于学生原有知识经验基础上的自我建构,原有的知识经验对新知的学习具有很重要的作用。学生头脑中的知识结构组织得越好,就越利于保存和应用。在教学中要特别重视沟通知识之间的内在联系。
首先,在课开始时的复习铺垫中,就紧紧抓住异分母分数加减与同分母分数加减之间的联系,通过强调同分母分数相加减分母不变只把分子相加减的算理,突出分母相同则表示分数单位相同,这样的分数才能直接相加减,暗示了异分母分数由于分母不同不能直接相加减的原因,给学生下一步的学习提供了一个合理的思维线路。其次,在课的结尾处,沟通了整数、小数、分数四则运算的内在联系。分数加减法与整数加减法、小数加减法的计算方法,从表面上看截然不同,但实质上含义完全相同。它们都有一个共同特点“相同计数单位的数才能相加减”。不论是整数加减法、小数加减法还是分数加减法,都要统一成相同的单位后才能进行计算。这样的深度沟通,有利于学生形成前后知识的结构化建构,完善学生的自我认知。

