一题七法唤神龙 谈笑风生皆鸿儒*——趣谈“话语权”的自然流失

●

(镇海蛟川书院,浙江 宁波 315200)

1 话题缘起

2014年3月，教育部发布了《关于全面深化课程改革，落实立德树人根本任务的意见》，提出把核心素养体系作为研究学业质量标准、修订课程方案和课程标准的依据，用于统领课程改革的相关环节，一时间，“核心素养”成为热门词汇，受到教育界广泛关注.“核心素养”以科学性、时代性和民族性为基本原则，以培养“全面发展的人”为核心，分为三大方面六大素养十八个基本要点，“点点”激起我们一线教师的思考.原本“四基”的课堂又面临着“精神”“人的意义”的生成和提升.中央民族大学孙晓天教授认为：数学素养真正变成学生的“素养”一定伴随着课堂教学方式的改变，让学生在自己的经历和体验中养成.笔者以一节习题点评课的实录为背景，描述下移课堂重心，把话语权“流放”给学生，有效放大教师和学生共同作为学习者的课堂体验.

2 “话语权”的自然流失与课堂生成

2.1 题目呈现

题目如图1，半圆O的直径AB=10，弦AC=6，AD平分∠BAC，求AD的长.

图1 图2

2.2 原汁原味，百家争鸣

笔者首先让学生在课堂上充分展示自己的想法，以下是学生的方法、思路展示.

生1：如图2，联结BC，交AD于点F，因为AB是直径，所以∠ACB=90°.又AC=6,AB=10,得BC=8.过点F作FG⊥AB于点G，则

AG=AC=6，

从而

GB=4.

设CF=GF=x，则

x2+42=(8-x)2，

解得

x=3，

于是

由CF·BF=AF·DF,得

从而

(此时不少学生发出“噢”的声音，紧接着就是一阵热烈的掌声.)

师：你是怎么想到的？

生1：我看到了条件中AB是直径，故联结BC交AD于点F，则∠ACB=90°.又因为AD是∠BAC的角平分线，联想到角平分线的性质定理，因此过点F作FG⊥AB.

师：非常好，生1从条件出发，找到了问题的突破口，这是我们解决问题的常用方法.要关注题目条件，并且要去联想与条件有关的知识，往往可以找到问题的突破口.

生2：如图3，在AB上取点E，使得AE=AC=6，则BE=4，显然△CAD≌△EAD，从而CD=DE.又因为AD平分∠BAC，所以CD=BD，于是DE=DB.过点D作DF⊥BE于点F，则

EF=BF=2，

从而AF=8.又因为AB是直径，所以∠ADB=90°，于是

AD2=AF·AB=80，

即

(学生们马上报以热烈的掌声.)

师：请说明你的思维过程.

生2：我也是看到了角平分线，想到之前常用的辅助线，截取线段长度相等，构造全等.而这里由圆周角相等，得到CD=DB=DE，则△DEB为等腰三角形，这时又想到等腰三角形中的常用辅助线，过点D作DF⊥EB，得到了我们熟悉的母子型，便可求解.

师：很棒!生2也是根据条件联想到相关基本模型，进行求解.我们平时也要像生2学习，掌握基本模型，并熟记于心，当碰到类似的条件时尝试着应用相关的基本模型，有时问题便迎刃而解.

图3 图4

于是

DH=2，

即

因为AB=10，所以

(学生们不约而同：“哇！”此时掌声更热烈.)

师：请阐述你的思维过程.

师：太棒了!本题是圆中的问题，有弧中点自然可以联想到圆中常见的基本模型，找到了问题的突破口.

(此时，有学生已经迫不及待地举手要分享自己的想法.)

图5

生4：如图5，延长AC,BD相交于点E，显然△BAD≌△EAD，从而

AE=AB=10.

由AC=6，得

CE=4，

又因为∠ECD=∠ABD，所以

△ECD≌△EBA,

从而

即

解得

于是

(“原来还可以这样做!”学生们惊叹，此时又响起了热烈的掌声，还没等笔者发问，生4已经在分享自己的解题思路了.)

生4：我就是看到角平分线又看到垂直，想起之前碰到过的问题，将图形补全，其实就是等腰三角形，这时根据圆内接四边形的一个外角等于与它不相邻的内对角，便可证相似.

师：同学们都很厉害！让我们一起来总结下，当条件中有角平分线时可以联想到用角平分线定理；可以截取线段长度相等，构造全等；当角平分线“邂逅”直角，可以补全图形，构造等腰三角形；当角平分线“邂逅”圆，可得弧中点，构造垂径定理基本模型.如果我们能在平时的学习中不断地像这样进行反思总结，就很容易找到问题的突破口.

生(这时有学生脱口而出)：老师，你之前还说过当角平分线遇到平行要关注等腰.

师：你提醒得太好了，反过来当等腰三角形碰到角平分线也会出现平行，比如这里△ODA为等腰三角形，AD平分∠BAC，则OD∥AC.

(当时笔者只是想让学生感受角平分线遇到平行会出现等腰，在这里却有了意外的收获.)

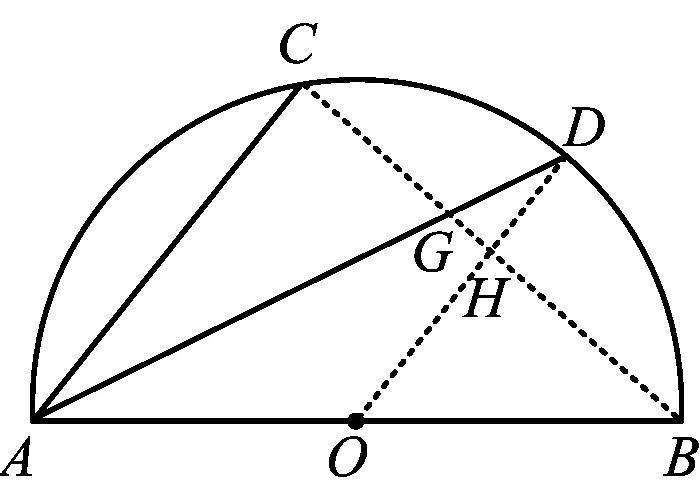
图6

生5：如图6，联结OD，因为△ODA为等腰三角形，AD平分∠BAC，所以OD∥AC.联结BC，分别交AD,OD于点G,H，则

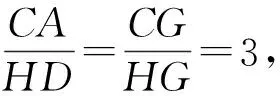
HG=1，CG=3，

从而

得

(学生们马上报以热烈的掌声.)

师：谢谢你给了我们一个惊喜，解决问题时，要多观察、多分析条件、多维度发散和联想，敢于尝试.

(此时还有学生在举手，有学生坐不住了，已经5种了，还有第6种解法？)

生6：如图7，过点O作OE⊥AC于点E，过点D作DH⊥OB于点H，联结OD，则

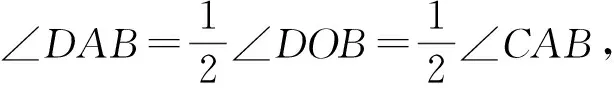
∠DOB=∠CAB.

又因为OA=OD，∠OEA=∠DHO=90°，所以

△OAE≌△DOH，

从而

OH=AE=3，DH=OE=4,

于是

AH=8，DH=4，

得

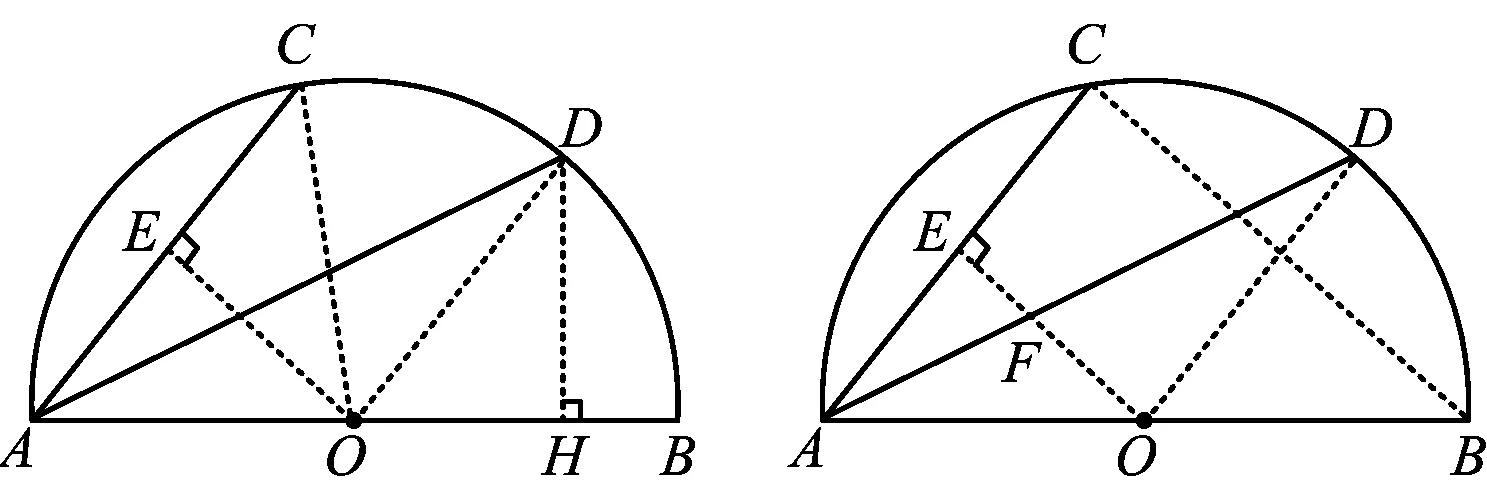
图7 图8

师：说说看，你是怎么想的？

生6：题中要求AD的长，我就想过点D作DH⊥OB于点H，如果能求出DH,AH的长，利用勾股定理，便可求解.因为对于圆中的弦，我们常过圆心作弦的垂线，构造垂径定理基本模型，这里我就想过点D作DH⊥OB，感觉△AEO≌△OHD，然后根据条件证明，发现两个三角形的确全等.

(“哇，这样也可以！”热烈的掌声马上响起.)

师：说得太好了！在解决问题时我们可以由因导果，从条件出发来找到问题的突破口，也可以执果索因，从结论出发，去寻求解决问题的线索，并且在解题过程中要有对图形的感知，大胆猜想.

(这时听到有学生小声嘀咕：“6种了啊，要是能凑7种方法就可以召唤神龙啦.”这时真有一个学生在举手发言.)

又EF+OF=4，得

从而

于是

(学生们异口同声说：“我们可以召唤神龙了！”紧接着学生马上报以雷鸣般的掌声.)

2.3 回收话语权——合理归纳，聚焦智慧

师：让我们来回顾刚才的解题过程，大家有什么收获？

生8：可以由已知条件联想到我们熟悉的模型或者知识点，进而产生思维的火花，或者从结论出发，去找问题的突破口.

师：非常好！为了解决问题，必须在我们的记忆中挑选和收集相关的知识，可以由因导果，也可以执果索因.那么我们平时在整理题目时要注意什么呢？

生9：注重基本知识的积累和整理，归纳基本模型，大胆尝试，条条大路通罗马.

师：你的理解之精辟，我要给你点赞.还有同学要分享吗？

生10：其实我认为几何题“猜”也很重要.

师：是的，所谓“猜”其实就是几何直观，我们可以借助几何直观将复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.

生11：我都没想到这题会有这么多解法，大家这么一讨论，我收获很多.

师：问题不辩不明，碰撞才会闪现火花.

(至此学生们对本题的方法、知识、思维层面已经有了深刻的认识.)

徐斌艳教授指出数学核心能力为数学提出问题、数学表征与变换、数学推理证明、数学建模、数学解决问题和数学交流等[1].一题多解，以不同的角度作为题目的切入口，多维度表征知识，有助于学习者发散思维，把握知识全貌，将知识融会贯通.一题多解是一种改变认知结构的良好工具，能够促进学生以一种全新的方式去建构知识.但是，教师如果仅仅让学生各自展示自己的方法，而没有关键时刻的点拨，那么只是空热闹一场，只有一时的繁华，而且学生的认知水平还停留在原有水平上.正如罗增儒教授所言：“萝卜炒萝卜还是萝卜，不可能有肉味”，教师要适时引导，将方法进行提炼，让学生豁然开朗，有所顿悟，体味“一览众山小”的感觉.因此一题多解不仅要关注学生思想方法的渗透，更要注重解决问题以后的优化提升及反思，对方法进行比较，探究问题的本质，挖掘通性通法，帮助学生培养理性的科学精神，渗透数学核心素养.

3 感悟反思

3.1 起点低，入口宽，落点高

本题题干简洁，却涵盖丰富的知识点，学生可以从多角度入手，可以由因导果，从已知条件出发进行思考，也可以执果索因，从结论出发进行思考.本题具有起点低、入口宽的特点，笔者让学生在课堂上充分展示自己对知识的理解和疑惑，引导大家共同讨论和交流，最终达成一致的理解，为学生提供展示其数学能力和数学素养的平台.

整个授课过程有学生上台展示，有生生之间、师生之间的问答，有教师的启迪引导，教学形式多样.课堂完全以学生为中心，教师进行角色让位，由知识的传授者变为课堂的引导者，创设了一种自由、和谐、民主、平等的课堂，让学生人人敢发言，鼓励学生探索与创新，调动学生学习的积极性，培养学生数学抽象、直观想象、逻辑推理等核心素养，激发学生自主探索、踏实钻研、合作交流的品格.

3.2 合理收放话语权，增强“信念系统”的作用

信念是个体的行为准则，来源于个体经验，通常无意识地影响新的经验，并指导个体行为.在数学学习过程中，每个学生都有自己的信念，这些信念构成一个体系，称之为数学信念系统，它指导着数学的个体活动、方式、行为以及数学的评价[2].当今数学问题解决理论强调“信念系统”在问题解决过程中的重大作用，即情感逻辑化作用.有些学生本来没有想到思路，但在活跃的课堂气氛中，当身边的同伴不断给出新的解题方法时，激发出求知欲，形成积极的内部情感动机，并开始调动自我内部关系，借助选择重构，将无意识思维活动质变为创造性情感活动，这时便会创造性发现新的方法.为了能让这种积极的情感体验增加有效期，教师可以让学生自己整理感悟收获，将感性的意识回流通过自我建构内化为自我信念系统.

3.3 经验跃迁，感悟升华素养精髓

数学活动经验很多都是内隐的.教学中，应该以经验助力积累新的经验，努力使隐形活动经验显性化，执教者要利用一切机会，引导学生将问题拓展、将知识方法结构化，升华已有的数学活动经验.《义务教育数学课程标准(2011年版)》指出：数学活动经验的积累是提高学生数学素养的重要标志，帮助学生积累活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.

有了上一次成功的经验后，笔者在以后的授课中，尽量有意识地多创造学生自主探究整理和分享的机会，每次都有意外的收获.

核心素养看似高大上，但真正要让核心素养落地生根，还是要靠教师课堂上的点滴渗透，下移课堂重心，将“话语权”流放给学生，如此核心素养已然在悄悄地生根发芽！

[1] 徐斌艳.数学学科核心能力研究[J].全球教育展望，2013(6):67-74.

[2] 刘展，屈聪.中学生数学信念系统与数学学习兴趣关系的研究[J].数学教育学报，2012，21(2):41-43.