打通纵横联系 巧构隐圆解题*

●

(新沂市第一中学，江苏 新沂 221400)

圆是一种非常完美的图形，具有很强的对称性和优美的性质.因此，若能借助圆的一些性质进行解题，往往能达到化难为易的效果.笔者在教学过程中发现，有很多表面上看起来与圆无关的问题，若能通过细致观察，实施一定的策略转化为圆的问题，则往往能达到意想不到的效果，突破解题的瓶颈.通过构造隐形的圆并转化为与圆有关的问题，体现了数形结合与化归转化的核心数学思想，是实现变式教学的重要途径与手段.下面笔者结合近几年来的各类试题，谈谈如何构造隐圆解题，现分析如下，供大家参考.

1 双变量问题

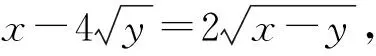
(2013年全国高中数学联赛试题第7题)

x=y+(x-y)=a2+b2(其中a≥0，b≥0),

a2+b2-4a=2b，

即

(a-2)2+(b-1)2=5(其中a≥0，b≥0).

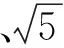
因此x=a2+b2的取值范围是[4,20]∪{0}.

评注本题含有两个变量与根式，通过观察发现两个根式的平方和即为所求.通过实施换元策略，转化为常见的点与圆的最值问题，从而降低了解题的难度.

图1 图2

2 函数最值问题

( )

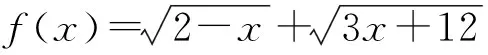
(2015年四川省高中数学联赛试题第4题)

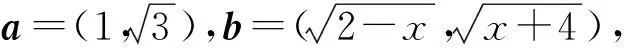
p2+q2=6(其中p≥0,q≥0).

f(x)=a·b=|a|·|b|cosθ=

评注本题借助平面向量，构造隐圆，转化为与圆有关的向量数量积问题，令人耳目一新.

3 解三角形问题

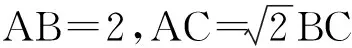
(2008年江苏省数学高考试题第13题)

即

(x-3)2+y2=8(其中y≠0)，

评注本题若用解三角形的方法求解，则复杂得多.通过建系，发现点在圆上运动，此圆是非常著名的阿波罗尼斯圆.这是源于课本的一道经典考题.

图3 图4

4 平面向量问题

( )

(2011年全国数学高考大纲卷第12题)

因为|a|=|b|=1，所以

OA=OB=1.

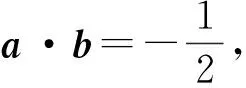
从而

即

∠AOB=120°.

又因为=60°，而120°+60°=180°，所以点O,A,C,B共圆.当OC为圆的直径时，|c|最大，此时

∠OAC=∠OBC=90°,

从而

Rt△AOC≌Rt△BOC,

得

∠ACO=∠BCO=30°,

于是

即

|OC|=2|OA|=2.

故选A.

评注向量因为其几何、代数双重身份而特殊，因为其双重身份而应用广泛，成为高考重点考查内容之一[1].若能注意到这一点，可结合图形思考，不难发现点O,A,C,B共圆，然后利用圆的性质和三角形全等的判定知识，实现问题的解决.

5 解析几何问题

例5已知⊙O:x2+y2=4，点P为直线x+2y-9=0上一动点，过点P向⊙O引两条切线PA，PB，A，B为切点，则直线AB经过定点

( )

C.(2,0) D.(9,0)

(2017年湖北省荆门、荆州、襄阳、宜昌七校联考数学试题第10题)

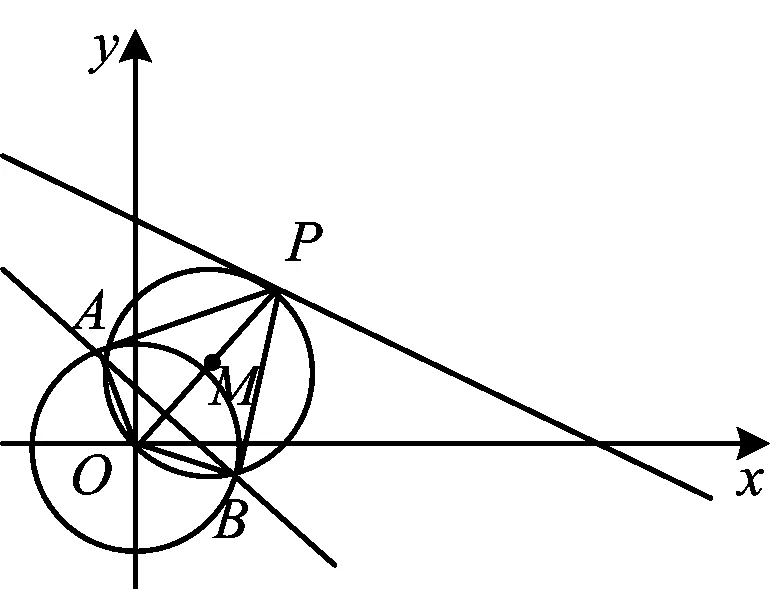
图5

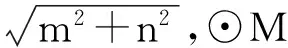
(x-m)2+(y-n)2=m2+n2，

即x2+y2-2mx-2ny=0.

(1)

又⊙O的方程为

x2+y2=4,

(2)

式(2)-式(1)，可得两圆的公共弦AB所在直线的方程为

2mx+2ny=4.

(3)

又因为点P(2m,2n)在直线x+2y-9=0上，所以

2m+4n-9=0，

即

2m=9-4n,

从而式(3)可化为

(9-4n)x+2ny-4=0，

即

2n(y-2x)+(9x-4)=0.

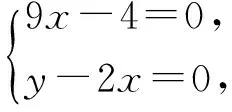
评注通过观察可以发现，点A,O,B,P共圆，同时可求出此圆的方程.于是AB即为两圆的公共弦方程，两圆方程相减，即可快速得到直线AB的方程.这是源于课本的重要方法，应引起足够的重视.

通过以上问题的分析，我们发现：构造隐圆解决数学问题是一种广泛运用于解题的方法.这种方法具有一定的可操作性，关键是通过认真观察，发现隐形的圆，使之为自己的解题服务.有些问题具有一定的数学文化背景，如例3；有些问题根植于课本而高于课本，如例5；有些问题打通了数学知识的内在联系，如例2.通过构造隐圆解决问题，不仅能开阔学生的思维与视野，提高解决问题的能力，还能使之体会到数学之美并提高学生的数学核心素养.

[1] 曹凤山.一个向量模 年年高考题[J].中学教研(数学)，2017(12)：43-46.