多视角探究条件、本质出解法、解法促延伸*

●

(同安第一中学,福建 厦门 361100)

怎么教会学生“一题多解”？笔者在解题教学实践中，认为试题解答可以“一题多解”的根源是条件(或设问)的不同使用视角．条件(或设问)的使用方式是解题的关键，条件(或设问)的不同使用方式会产生不同的解法．

解题者使用条件(或设问)的方式归结起来主要有以下3个视角：1)观察条件(或设问)中的数、式、图、点等的特征，对条件(或设问)的不同观察视角发现不同的特征，从而产生不同的解法；2)抓住条件(或设问)的内涵外延，对条件(或设问)的不同理解层次导向不同的思路，从而产生不同的解法；3)从思考数学问题的思维倾向入手，依问题选思维视角，用思维找切入口，不同思维视角产生不同的解法．

笔者以学生较为薄弱的圆锥曲线问题作为示例，以一道高考试题作为模本来展示条件(或设问)的不同使用视角而产生的不同解法，并对该题进行变式引申、情境迁移、条件变换，从而探究类似的新结论，挖掘类似的新命题，再用类似的视角去透视延伸出来的新问题，让同类题串可用同类视角串加以分析解决．

例1已知F为抛物线C:y2=4x的焦点，过点F作两条互相垂直的直线l1，l2，直线l1与C交于点A，B，直线l2与C交于点D，E，则|AB|+|DE|的最小值为

( )

A．16 B．14 C．12 D．10

(2017年全国数学高考新课标卷Ⅰ理科试题第10题)

1 多视角探寻解法

1.1 从直线代数特性的视角进行透视

视角1理解设问中的|AB|+|DE|，发现|AB|,|DE|是焦点弦，可以利用焦点弦公式求弦长．利用两条直线垂直的代数特征呈现斜率关系，其斜率是负倒数关系，发现直线过定点，可设直线方程为点斜式，直接计算．

得

k2x2-(2k2+4)x+k2=0.

设A(x1,y1)，B(x2,y2)，则

同理可得

|DE|=4+4k2,

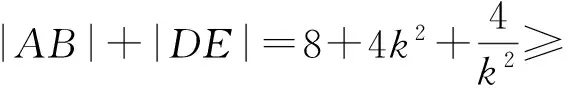
当且仅当k=±1时,等号成立．

视角2理解设问中的|AB|+|DE|，发现|AB|,|DE|是抛物线的弦，可以利用弦长公式直接求弦长．发现直线所过的定点在x轴上，可设形如x=my+n的直线方程形式，简化计算过程．

y2-4ty-4=0.

设A(x1,y1)，B(x2,y2)，则

y1+y2=4t,y1y2=-4，

利用弦长公式求得|AB|=4(t2+1)，同理可得

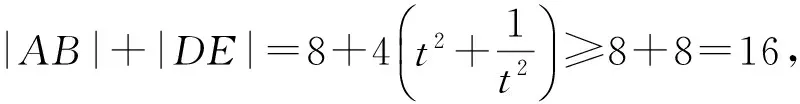
当且仅当t=±1时，等号成立．

视角3理解设问中的|AB|+|DE|，发现线段AB可以分解为同一直线上的两条线段AF,BF之和.符合这一特性的线段求长度，可利用直线参数方程中的参数几何意义来求解．同理线段DE可以分解为同一直线上的两条线段DF,EF之和，也可利用直线参数方程中的参数几何意义来求解．发现两条直线相交于定点F(1,0)，由两条直线垂直可知它们的倾斜角存在等量关系，从而可以统一设出这两条直线的参数方程．

解法3(直线的参数方程)设直线AB的倾斜角为θ，则直线AB的参数方程为

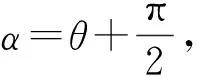
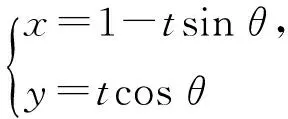
sin2θ·t2-4cosθ·t-4=0,

设此方程的两根为t1和t2，则

从而 |AB|2= |t1-t2|2=(t1+t2)2-4t1t2=

于是

图1

视角4理解设问中的|AB|+|DE|，发现|AB|,|DE|是焦点弦，要求焦点弦的长度，发现|AB|可转化为焦半径之和，因而研究焦半径如何表示即可．由于两条直线垂直，发现其倾斜角互补，容易想到引入倾斜角作为参数，结合抛物线定义即可用角表示焦半径的长．

解法4(焦点弦的倾斜角公式)设直线AB的倾斜角为θ,如图1，过点A作x轴的平行线，与抛物线C的准线交于点K1，过点A作AK2⊥x轴于点K2．由抛物线定义得

|AF|= |AK1|=|GF|+|FK2|=p+|FK2|=

p+|AF|cosθ，

从而

同理可得

因此

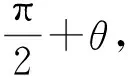
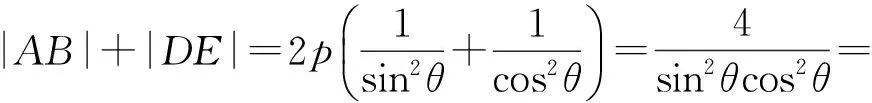
1.2 从线段的几何视角进行透视

视角5对设问中的|AB|+|DE|作整体理解，发现这是求线段和或线段差的最值问题．变换思维逆向推理，把问题转化成平面几何的视角，利用平面几何中求线段和的方法，把分散的线段迁移到较为集中的线段，然后求和差.借助圆锥曲线定义实现线段迁移，从而把代数问题转化为平面几何问题，只需利用数形结合思想便能迎刃而解．

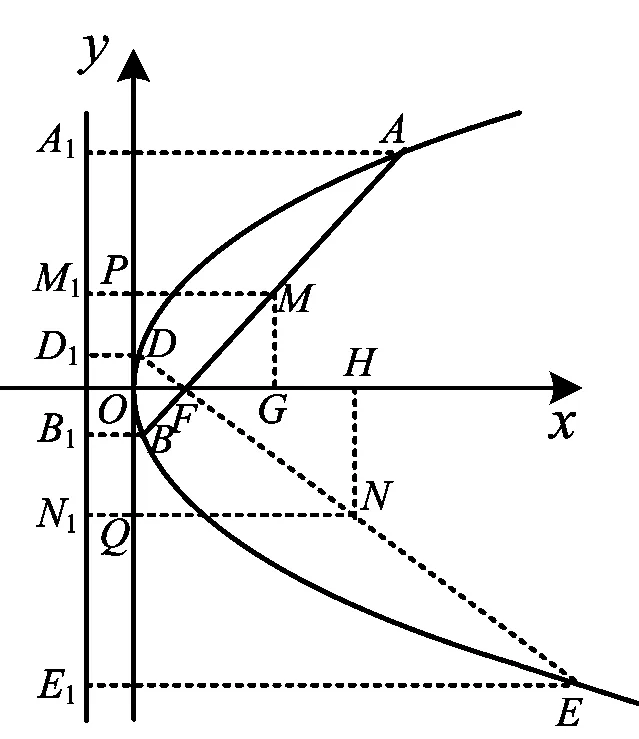
图2

解法5(焦点弦的几何性质)取线段AB,DE的中点M,N，如图2，分别过点A,B,D,E,M,N作准线x=-1的垂线，垂足分别为A1,B1,D1,E1,M1,N1；过点M,N作x轴的垂线，垂足分别为G,H．由抛物线的定义，得

|AB|+|DE|=

(|AF|+|BF|)+(|DF|+|EF|)=

(|AA1|+|BB1|)+(|DD1|+|EE1|)=

2(|MM1|+|NN1|)=2(|MP|+|NQ|+2)=

2(|OG|+|OH|+2)=2(|FG|+|FH|+4)=

因为∠MFN=90°,所以△MFG≌△FNH,从而

于是

|FG|·|FH|=|MG|·|NH|.

当且仅当|MG|=|NH|，即|FG|=|FH|时，等号成立，此时

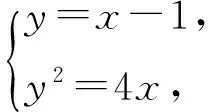
yM=2,

同理可得

yN=2.

1.3 从抛物线方程的视角进行透视

视角6理解设问中的|AB|+|DE|，发现|AB|,|DE|的本质特征就是两点间的距离，可以直接利用两点间的距离公式来解．理解题目条件，发现4个点都在抛物线上，若直接设出点的坐标(x,y)，那么求解过程会带来繁琐的计算.为了减少字母运算，联想设点坐标的其他形式，容易想到用参数方程来设点坐标．

解法6(抛物线的参数方程)因为抛物线y2=4x的参数方程为

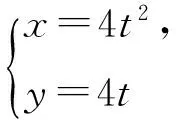
kAF=kBF,

即

于是

同理可得

由AB⊥DE,得

kAB=kDE，

从而

即

(t1+t2)(t3+t4)=-1，

于是

同理可得 |DE|=4[1+(t4+t3)2].

令t2+t1=m，则

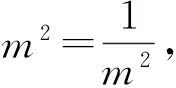
视角7理解设问中的|AB|+|DE|，发现线段AB和DE的一个关联特征是线段AB和线段DE相交，因此|AB|+|DE|可以转化为4条线段AF，BF，DF，EF之和.又发现这4条线段具有公共点且公共点在x轴上的另一特征，符合建立极坐标系的情景及利用极径表示线段长度的特性，从而行之有效地把在直角坐标系中求线段长的问题迁移到了新的坐标系中．

图3

解法7(抛物线的极坐标方程)以点F(1,0)为极点、射线Fx为极轴建立极坐标系.如图3，设P(ρ,θ)为抛物线上任一点，抛物线的准线为l:x=-1，作PH⊥l于点H,PM⊥x轴于点M.由抛物线的定义得

|PF|=|PH|，

从而|PF|=|GM|=|GF|+|FM|,

于是

ρ=2+ρcosθ，

即

设点A的极坐标为(ρ1,θ)，则

从而 |AB|+|DE|=ρ1+ρ2+ρ3+ρ4=

1.4 从解题思维的视角进行透视

视角8深刻理解条件中的直线内涵，发现两条直线存在运动变化的特征，即过定点的两条直线在运动变化中保持相互垂直.依据“运动变化的直线最值问题一般都是在特殊位置时取到”的思路进行探究，又发现两条直线是在抛物线的情境下运动变化的，寻求两条直线相对特殊位置应从抛物线的图像特征着手，联系抛物线的图像对称性就可发现特殊位置，最后通过先猜后证的思想加以解决．此视角围绕条件和设问，遵循了“猜得有目标、猜得有依据”的数学直觉思维．

解法8(直觉思维、先猜后证、特殊到一般)由于抛物线关于x轴对称，两条直线都过x轴上的同一个定点F，抓住“定点在抛物线的对称轴上”这一特征，容易联想到从对称的角度去寻找两条直线的相对特殊位置，自然而然也会猜想到当l1和l2关于x轴对称时，|AB|+|DE|取到最小值，此时k1+k2=0.又k1k2=-1，从而k1=±1，容易算得

|AB|=|DE|=8，

因此|AB|+|DE|可取到最小值16(证明略)．

2 启发思索

探究1基于该题的解析几何情景、条件设置、研究方向，是否可以进行变式延伸探究？是否可以进行迁移情景类比探究？

2.1 设问拓展产生变式延伸题

2.2 背景类比产生情境迁移延伸题

圆锥曲线具有统一性、圆锥曲线问题具有背景迁移性，启发我们可以将本题的抛物线迁移到椭圆、双曲线中进行类比探究，如下面漂亮的“蝶形”问题：

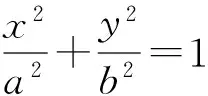
3 条件变换产生延伸题、延伸题再情境迁移成新延伸题

3.1 增设常见条件、背景一般化，再迁移到“孪生曲线”类比探究

例3已知F为抛物线C:y2=2px(其中p>0)的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于点A，B，直线l2与C交于点D，E.设AB,DE的中点分别为M,N，求证：直线MN经过一个定点．

3.2 背景一般化，再迁移到“姐妹曲线”类比探究

1)求证：

2)求四边形ADBE面积的取值范围．

3.3 背景一般化，可迁移情境类比探究

例5已知F为抛物线C:y2=2px(其中p>0)的焦点，过F作两条直线l1,l2，直线l1与C交于点A，B，直线l2与C交于点D，E，直线l1，l2的斜率之积为m(其中m≠0)，求四边形ADBE面积的最小值．

探究2类似以上的变式迁移题，能否依然借助例1所用的解题视角进行分析破解？答案是肯定的，读者可以自行选取几个视角进行探究(本文略)．

4 解题感悟与启示

立足于圆锥曲线情境，研究在一种几何条件限制下的解析几何问题，通过多视角透视几何条件(或设问)探寻多角度的解法，提炼处理这类几何条件的解题策略．善于在同一背景下重新审视问题，拓展变式问题，也许会发现新结论；善于变换条件推广问题，也许会发现内在关联性；善于进行情境迁移探究，也许会发现一般规律性．延伸拓展问题后，再次选用解决“母题”的视角去探究它们，往往能发现探究过程具有异曲同工、殊途同归之妙，解答过程往往又能展现情境、模型、解法归一之美！