坡代数的区间值模糊理想

王丰效

WANG Fengxiao

喀什大学 数学与统计学院，新疆 喀什 844000

College of Mathematics and Statistics,Kashigar University,Kashi,Xinjiang 844000,China

1 引言

坡代数是由控制论专家曹志强提出的[1]，关于坡代数的相关概念和理论在曹志强与Kim和Roush合著的专著[2]中给出了详细的介绍。坡代数及坡代数上的矩阵理论在自动机理论、控制论、神经系统等领域有着很好的应用前景。1965年，Zadeh创立了模糊集的理论[3]。Rosenfeld提出了模糊子群的概念[4]，标志着模糊代数研究进入了一个新的领域。随后模糊集的理论被广泛应用于代数系统，并取得了丰富的研究成果。Jun等将模糊集的理论应用于坡代数，给出了坡代数的模糊子坡代数和模糊理想的概念，得到了坡代数的模糊子坡代数和模糊理想的若干等价条件和性质[5]。文献[6]和[7]讨论了坡代数的直觉模糊理想和坡代数的T-模糊理想。随后，许多学者对坡代数进行了一系列的研究，取得了丰富的研究成果[8-11]。文献[12]将模糊集的概念推广到区间值模糊集（Interval-Valued fuzzy set，I-V模糊集），文献[13]讨论了半群的I-V模糊理想，文献[14]研究了N（2，2，0）代数的I-V模糊子代数，文献[15]研究了布尔代数的I-V模糊理想。本文将I-V模糊集的概念应用到坡代数，给出了坡代数的I-V模糊理想的概念，并讨论了其相关基本性质，为今后深入研究坡代数创造了必要条件。

定义1[2]设X是一个集合，若+和*是X上的两个二元运算，且对任意x,y,z∈X满足以下条件：则称(X,+,*)为坡代数。

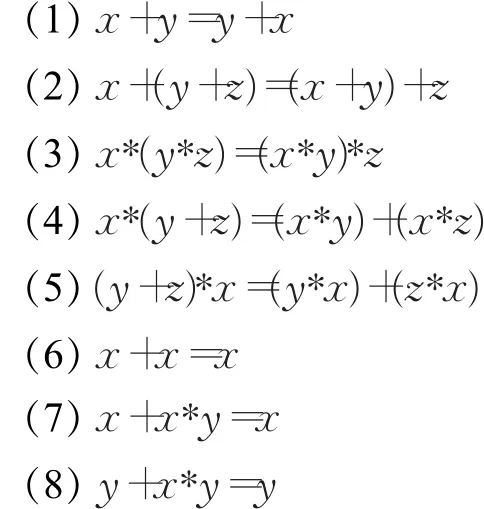
设(X,+,*)为坡代数，在X上定义关系≤如下：对任意x,y∈X,x≤y当且仅当x+y=y，则≤是X上的一个偏序关系。

定义2[2]设(X,+,*)和(Y,+,*)是坡代数，f:X→Y为映射。若对于任意x1,x2∈X，有：

成立，则称 f:→Y为从X到Y的同态。

定义3[6]设(X,+,*)是坡代数，A是X上的模糊集，若对于任意x,y∈X有：

A(x+y)∧A(x*y)≥A(x)∧A(y)则称A是X的模糊子坡代数。

定义4[6]设(X,+,*)是坡代数，A是X的模糊子坡代数，并且若x≤y有A(x)≥A(y)，则称A是X的模糊理想。

称aˉ=[a-,a+]⊆[0,1]为区间数，用 D[0,1]表示区间数的集合。对于D[0,1]中的两个元素可以定义加细极小（记为γmin），并且规定D[0,1]中元素的大小。D[0,1]中元素，规定：

设X是非空集合，X上的一个区间值模糊集（I-V模糊集）定义为：

2 坡代数的I-V模糊理想

定义5设(X,+,*)是坡代数，Aˉ是X上的I-V模糊集，并且满足：

如无特殊说明，在不致引起混淆的情况下，X总表示一个坡代数。

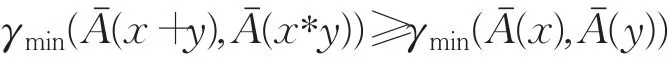
由区间数的大小定义可知：

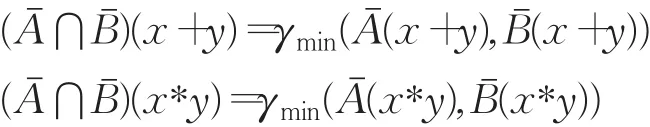
从而

3 坡代数的I-V模糊理想的直积和同态像

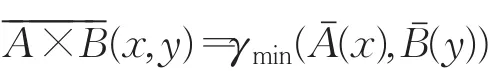
引理1设(X,+,*)和(Y,+,*)是两个坡代数，在X×Y上定义两种运算加法+和乘法*如下：对任意(x1,y1),(x2,y2)∈X×Y ，规定：

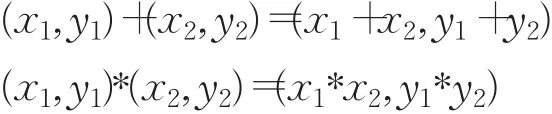
则X×Y关于上述两种运算构成一个坡代数。

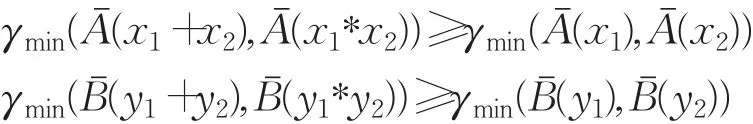
并且若(x1,y1)≤(x2,y2)，这里(x1,y1)≤(x2,y2)是指x1≤x2，y1≤y2，因此有：

先证明如果(x1,y1)≤(x2,y2)，则：

事实上，由于：

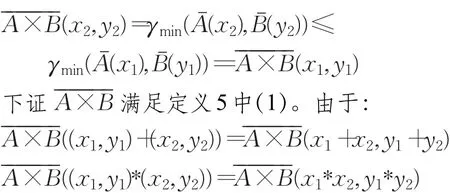
定理4设(X,+,*)和(Y,+,*)是两个坡代数，f:X→Y为同态满射，并且映射 f单增。如果是X的I-V模糊理想，则 f(Aˉ)是Y 的I-V模糊理想。其中

证明 对于任意的y1,y2∈Y，由于 f是X到Y的同态满射，故存在x1,x2∈X，使得：

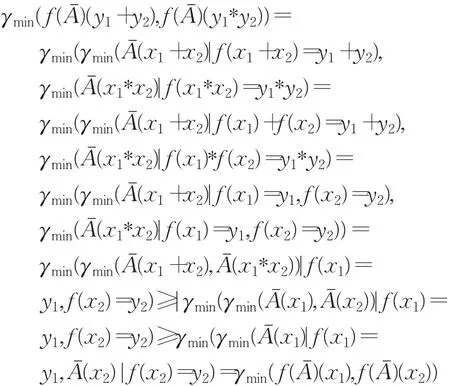
若 x1≤x2，f(x1)=y1,f(x2)=y2，映射 f单增，所以y1≤y2。故

4 结束语

本文将区间值模糊集的思想和概念应用于坡代数，给出了区间值模糊理想概念，讨论了坡代数的区间值模糊理想的相关性质以及坡代数区间值模糊理想的同态像的相关性质，得到了一些有意义的结论。这些结论不但有助于进一步把握坡代数的模糊结构特征，而且也有助于促进区间值模糊集理论与坡代数理论间的相互融合。同时，本文所运用的研究方法对于其他代数系统类似问题的研究具有一定的借鉴意义。

参考文献：

[1]Cao Zhiqiang.A new algebraic system—slope[J].Busefal，1981，6：22-27.

[2]Cao Zhiqiang，Kim K H，Roush F W.Incline algebra and applications[M].New York：John Wiley，1984.

[3]Zadeh L A.Fuzzy sets[J].Information and Control，1965（8）：338-353.

[4]Rosenfeld A.Fuzzy groups[J].Journal of Mathematical Analysis and Applications，1971（35）：512-517.

[5]Jun Y B，Ahn S S，Kim H S.Fuzzy subinclines（ideals）of incline algebras[J].Fuzzy Sets and Systems，2001，123（2）：217-225.

[6]Ma Xueling，Zhan Jianming.Intuitionistic fuzzy ideals of incline algebras[J].Scientiae Mathematicae Japonicae，2005，62（1）：33-38.

[7]Zhan Jianming，Long Ming.T-fuzzy ideals of incline algebras[J].Scientiae Mathematicae Japonicae，2005，61（1）：67-73.

[8]刘璐璐，伏文清，李生刚.模糊子坡代数、模糊等价关系及模糊同余关系的序方面[J].模糊系统与数学，2011，25（5）：43-49.

[9]刘璐璐，伏文清，李生刚.模糊子坡代数、模糊理想、模糊滤子及模糊同余关系的刻画[J].山东大学学报：理学版，2011，46（11）：48-52.

[10]赵虎，李生刚，陈桂秀.坡代数上的模糊软子坡[J].吉林大学学报：理学版，2013，51（4）：555-560.

[11]王丰效.布尔代数的（λ，μ）模糊子代数[J].高校应用数学学报：A辑，2011，26（4）：495-500.

[12]Hong S M，Jun Y B，Kim S J.Fuzzy BCI-subalgebras with interval-valued membership functions[J].International Journal of Mathematics and Mathematical Sciences，2001，25（2）：135-143.

[13]陈露.半群的I-V Fuzzy理想[J].纯粹数学与应用数学，2009，25（1）：102-106.

[14]王丰效.布尔代数的I-V模糊理想[J].模糊系统与数学，2017，31（3）：49-54.

[15] 王丰效.N（2，2，0）代数的I-V模糊子代数[J].黑龙江大学自然科学学报，2017，34（3）：301-304.