尊重学生认知 尊重数学本真——“直角三角形的性质”教学设计

张玲玲

（上海市梅陇中学）

一、教学解析与设计

本节课的教学内容是上海教育出版社《义务教育教科书·数学》八年级上册第十九章中“直角三角形的性质”的第1课时.学生在七年级的时候，已经学习并掌握了等腰三角形的判定与性质，这为我们研究特殊的三角形提供了一定的认知基础和学习范式.此前，对于直角三角形，学生只学习过它的定义及其有关概念，以及两个直角三角形全等的判定.而这一节课要研究的就是直角三角形的性质.

定理1：直角三角形的两个锐角互余.

定理2：直角三角形斜边上的中线等于斜边的一半.

这两条性质分别揭示了直角三角形的主要元素“角”之间的数量关系，主要元素“斜边”及相关元素“斜边上的中线”之间的数量关系，这是本节课的学习主题与重点.同时，无论是定理2的文字语言表述，还是图形语言的描述，都揭示了直角三角形与等腰三角形之间内在的天然联系，这种联系在例题、练习题中，同样显示得那么强烈.

性质定理2是后续研究直角三角形与特殊平行四边形的基础与依据，直角三角形与等腰三角形的联系与转化也是解直角三角形的利器.对于这两条性质的学习为今后学习平面几何的证明奠定了坚实的基础.

由于两条性质定理是本课时的学习主题与重点，于是制定：（1）掌握直角三角形的两个锐角互余的定理；（2）初步掌握直角三角形斜边上的中线等于斜边的一半的定理，并能初步运用，作为这节课的第1，2教学目标.鉴于对从一般到特殊、从特殊到一般的数学思想，以及特殊化、一般化策略的认识，对小组合作学习功能发挥的认识，设置了经历“直角三角形斜边上的中线等于斜边的一半”探究和推导的证明过程，体会从一般到特殊，再从特殊到一般的数学思想方法，并从中分享小组合作探究成功的喜悦为第3教学目标.出于对充分发挥教学内容本身具有的育人功能的认识，设置了第4教学目标：通过多媒体动态变化过程的演示，定理证明、例题解析、习题演练这些过程中两类图形具有规律性的呈现，认识到变化与不变、一般与特殊、联系与转化是世界上事物普遍性的反映.

在本节课的学习过程中，学生会遇到一些困难和问题.首先，在这两条性质中，两锐角互余学生容易探究得到.但是，对于斜边上的中线等于斜边的一半，学生很难自主探究得到.为什么是斜边上的中线，而不是其他两条直角边上的中线？为什么这条中线恰好等于斜边的一半？这些都是“横”在学生探索新知途中的“坎”.其次，虽然获得了这个结论，但是如何证明这个结论，对于学生来说也是比较困难的.基于以上两点，笔者把本节课的教学难点设置为直角三角形斜边上的中线性质定理的探究和推导.

二、教学过程设计

整个教学过程由复习引入、探求新知、例题选讲、课堂练习、自主小结5个环节构成.而4个教学策略则融合在这5个环节内有序进行.

1.复习引入

运用教学策略1：从特殊与一般的相互转化中展现学习主题.

具体转化过程如图1所示.

图1

这里特殊化、一般化的研究策略，旨在让学生更好的理解这两条性质的发生.

2.探求新知

运用教学策略2：从图形的动态变化中概括图形的不变性.

（1）直角三角形性质定理1.

问题1：将等腰直角三角形变化为一般的直角三角形（如图2），这时，两锐角∠A与∠B还都等于45°吗？如果不是，那么这两锐角之间存在怎样的数量关系呢？

图2

答：∠A，∠B都不等于45°；由∠A+∠B+∠C=180°，∠C=90°，可得∠A+∠B=90°，即∠A与∠B互余.

问题2：如果用文字语言表述，可以得出怎样的一个真命题？

答：直角三角形的两个锐角互余.

定理1：直角三角形的两个锐角互余.

用符号语言表示如下.

因为在Rt△ABC中，∠C=90°（已知），

所以∠A+∠B=90°（直角三角形的两个锐角互余）.

（2）直角三角形性质定理2.

问题3：我们发现等腰直角三角形底边（斜边）上重合的三条线段（中线、高线和顶角平分线）都等于底边（斜边）的一半，那么：

①在一般的直角三角形中，这三条线段还会都等于斜边的一半吗？

②这三条线段中有没有一条线段等于斜边的一半呢？如果有，是哪一条？

③如何证明？

答：①不会；

②有，其中斜边上的中线等于斜边的一半；

③略.

学生很快探究得到性质定理2的结论：直角三角形斜边上的中线等于斜边的一半.但是，如何证明，也是本节课的一个难点.

已知：如图3，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线.求证：CD=AB.

为了更好地激发学生的有序思维，设计了下面的问题.

问题4：如图3，①根据题中的已知条件和现有的图形你能直接证明CD=AB吗？不添加辅助线行吗？

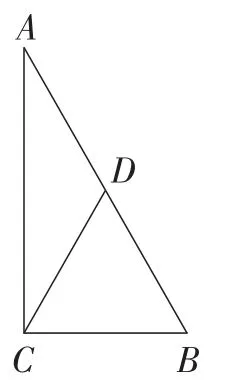
图3

②添加怎样的辅助线？

③这样添加辅助线的目的是什么？

答：①不能，不行.

②倍长中线.

③将证明线段的倍半关系转化为证明线段的相等关系.

很快学生找到了解决问题的突破口.学生分析完毕后，展示证明过程.

证明：如图4，延长CD到点E，使DE=CD，连接AE.

因为CD是斜边AB的中线，

所以AD=BD（三角形中线的定义）.

因为在△AED与△BCD中，

图4

所以△AED≌△BCD（SAS）.

所以AE=BC（全等三角形对应边相等），

∠3=∠B（全等三角形对应角相等）.

因为∠ACB=90°（已知），

所以∠4+∠B=90°（直角三角形中两锐角互余）.所以∠4+∠3=90°（等量代换），

即∠CAE=∠ACB（等量代换）.

因为在△CAB与△ACE中，

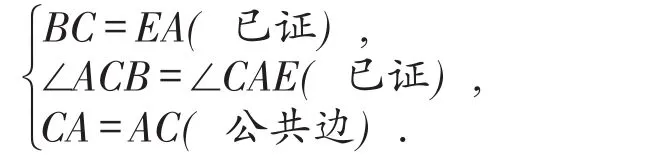
所以△CAB≌△ACE（SAS）.

所以AB=CE（全等三角形对应边相等）.

由此得到另一个定理.

定理2：直角三角形斜边上的中线等于斜边的一半.

符号语言表示如下.

在Rt△ABC中，因为∠ACB=90°，CD是斜边AB上的中线（已知），所以CD=AB（直角三角形斜边上的中线等于斜边的一半）.

3.例题选讲

运用教学策略3：精选、精讲、精析，发挥例题的多重功能.

此题主要是性质定理2的简单运用，同时给出了证明的规范步骤.例如，标记“★”的两步.

例 如图5，在△ABC中，AD⊥BC，垂足是点D，点E，F分别是AB，AC的中点，且DE=DF.求证：AB=AC.

证明：因为AD⊥BC（已知），

所以∠ADB=∠ADC=90°（垂直的定义）.★

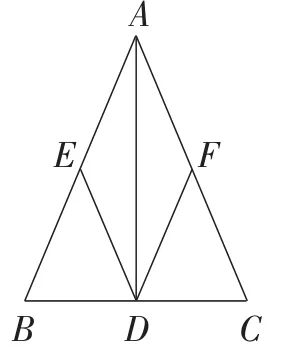
图5

因为E是AB的中点（已知），

边的一半）.

因为DE=DF（已知），

所以AB=AC（等式性质）.

在例题讲解完毕后，再运用教学策略4：展示图形的分割、拼合，用图形语言揭示联系、转化.

问题5：①细看图3，以直角三角形斜边上的中线为公共边的两个三角形是什么三角形？

②如何用“分割”这个词来表述从直角三角形得到等腰三角形的过程？

③细看图5，如何用“分割”这个词来表述从等腰三角形得到直角三角形的过程？

④反之，又如何用“拼合”这个词来表述？

答：①两个等腰三角形；

②直角三角形斜边上的中线将它分割成两个等腰三角形；

③一个等腰三角形可以分割成两个全等的直角三角形；

④两个全等的直角三角形可以拼合成一个等腰三角形；两个腰相等并且顶角互补的等腰三角形可以拼合成一个直角三角形.

4.课堂练习

已知，如图6，BE，CF分别是△ABC的高，D是BC的中点，连接DE，DF.求证：△DEF是等腰三角形.

图6

证明：略.

此题是对直角三角形斜边上的中线性质定理的简单运用.其设计意图有以下三点：（1）让学生对这一性质进行巩固；（2）此题能检测学生是否观察到了共斜边但不共直角顶点的两个直角三角形；是否注意到了长度相等但不重合的斜边上的中线；是否发现产生了一个“新生”的等腰三角形；（3）可以更进一步深刻的体会到直角三角形和等腰三角形之间内在的天然联系.

5.自主小结

自主小结主要内容如图7所示.

图7

通过这节课的学习，首先，学生最直接的收获是直角三角形的两条性质.其次，用分割和拼合来描述直角三角形和等腰三角形之间的天然联系.然后，还感受到从一般到特殊，从特殊到一般的研究数学问题的思想方法.但是要想悟出其背后隐含着的联系与转化、变化与不变、一般与特殊这三个理解世界事物的大道理，可能还需要教师的点拨.

三、教学反思

通过对这一节课的反复磨课、专家点评后，笔者领悟到一个优秀的、成功的、能打动人的教学设计，必须基于两点：尊重学生认知；尊重数学本真.

而这一节课开篇就是从学生已有的认知基础——等腰三角形的性质出发，唤醒了学生已有的等腰三角形的认知，然后利用等腰直角三角形这个特殊的等腰三角形（也是特殊的直角三角形），作为知识的桥梁，沟通等腰三角形和直角三角形之间的联系，从而自然引发学生对直角三角形性质探究的兴趣.同时也使其体会了从一般到特殊，再从特殊回到一般的研究问题的数学思想方法.而在这里特殊化、一般化的研究策略，旨在让学生更好地理解这两条性质的发生.这里既体现了尊重学生的认知基础——思维脉络的发展，又体现了尊重数学的本源——知识脉络的发展.

在探究直角三角形性质的过程中，利用多媒体课件的设计，在直角三角形这个图形的动态变化过程中，给学生以强烈的视觉冲击，使他们直观的视觉感知和理性的认知基础有机融合，从而感受图形中不变的特征.而图形不变的特征，本质上就是直角三角形的性质.在课堂上，学生很快发现了其本质的特征，直角三角形两锐角互余；直角三角形斜边上的中线等于斜边的一半，并能对这两类关系进行口头表述.

为了引导学生发现直角三角形斜边上的中线把直角三角形分成了两个等腰三角形，从中让学生慢慢体会这两种特殊三角形之间存在着的内在的天然联系.而我们知道图形的分割是将一个图形一分为二，图形的拼合是将两个图形合二为一，这是改变图形的两种互逆的思维方式.于是，设计了一组问题（问题3），以便学生能更深入地思考、体会这两种特殊三角形之间的联系.

无论是从开始的引入，还是探究的过程，乃至后来的小结，都是围绕直角三角形与等腰三角形这两种特殊三角形的内在联系进行展开的，环环相扣、步步逼近.始终以学生的认知基础、认知心理，以及数学知识本身的内在联系为线索，并且使这两条线索有机融合，从而让学生获取知识、提高能力变得水到渠成.

当然，好的教学需要给学生留白，需要留给学生足够多的思维空间.这方面，在这节课上比较欠缺.例如，在对一般的等腰三角形进行特殊化时，可以更放开一些，留给学生思考：你能否将这个等腰三角形进行特殊化？这里无非是两种可能：边特殊化——等边三角形，这个我们已经研究过；角特殊化——顶角为直角.完全可以提出问题，让学生进行自主思考，使学生逐渐具有完备的数学思维体系.同样，在后面的几个环节中，教师如果能再少讲一点，让学生再多思考一点，进而能产生连续的自主思维，那就更好了.

作为一名数学教育工作者，笔者将把尊重学生认知，尊重数学本源作为今后教学的出发点，使其成为笔者今后数学教育的“铁律”.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.