感受类比 生成概念——“从分数到分式”教学设计

李娟娟

（新疆乌鲁木齐市第二十九中学）

一、内容和内容解析

1.内容

“从分数到分式”选自人教版《义务教育教科书·数学》八年级上册（以下统称“教材”）第十五章“分式”第1课时，主要内容为分式的概念及分式有意义的条件.

2.内容解析

分式的分母表示除数，由于除数不能为0，因此分式的分母不能为0，即分式有意义的条件是分母不为0.

从运算的角度看，分式表示两个整式相除的商，这与分数表示两个整数相除的商类似.因此，分式与分数具有相似的基本性质和运算法则，以及相似的研究思路和方法.但是分式比分数更具有一般性，即分数是分式中字母取一些特殊值时的结果.

通过与分数的类比引入分式的概念，并利用类比的数学思想理解分式概念的基本特征；通过概念的实际背景及其应用，体会分式的建模思想，由数到式的演变体现从具体到抽象、从特殊到一般的思想方法.

基于以上分析，确定本节课的教学重点：分式概

二、目标和目标解析

1.目标

（1）了解分式的概念及分式有意义的条件.

（2）在类比分数抽象分式的概念及探索分式有意义的条件的过程中，体会类比的数学思想，感悟从具体到抽象、从特殊到一般的研究问题的方法.

（3）在数学学习过程中养成独立思考、合作交流、反思质疑等学习习惯.

2.目标解析

达成目标（1）的标志是学生能判断一个代数式是否是分式，能确定使分式有意义的字母的取值范围.

达成目标（2）的标志是学生能够类比分数得到分式的概念，在利用表格中的数据研究分式有意义的过程中，感悟从具体到抽象、从特殊到一般的研究问题的方法.

达成目标（3）的标志是学生能独立思考，愿意与同伴合作交流，分享自己的想法，并能够进行反思与质疑.字母，那么式子

念及分式有意义的条件.

三、教学问题诊断分析

学生可以通过解决实际问题获得新的代数式，但是通过观察代数式的结构特征，抽象出共同的本质属性是有一定困难的.关键是要引导学生通过与分数进行类比，从式子的形式上寻找它们的共同点.再从分子、分母单独看，分式的分子、分母都是整式，并且分母中都含有字母，通过这个过程经历从特殊到一般、从具体到抽象的思维过程，实现从分数到分式的过渡，从而归纳出分式的概念，体会研究代数问题的一般思路.

本节课的教学难点是分式概念的形成.

四、教学过程设计

1.创设情境，感受新知

幻灯片播放新疆喀纳斯景区的美丽图片：每年一到9月，新疆喀纳斯就进入了黄金时节，天高云淡、层林尽染、远处的雪山、近处的美湖、漫步的牛羊、小木屋的炊烟袅袅，呈现出一个童话般的五彩世界！今年九月我终于踏上了喀纳斯之旅……

问题1：我们到达乌鲁木齐机场，办理完登机手续后还有时间，便走进了一家新疆特产店，映入眼帘的是墙上一幅面积为8 000 cm2的具有民族特色的挂毯，长为110 cm，则宽为_______；

若有一个长方形的面积为S，长为a，则宽为____.

问题2：乌鲁木齐到喀纳斯的航程为540千米，飞机无风时的平均航速为580千米/时，若当天风速为30千米/时，从乌鲁木齐逆风飞往喀纳斯，则____小时到达喀纳斯机场.

乌鲁木齐到喀纳斯的航程为540千米，飞机无风时的平均航速为580千米/时，若当天风速为v千米/时，从乌鲁木齐逆风飞往喀纳斯，则_____小时到达喀纳斯机场.

问题3：午饭时我们品尝了烤鱼，喝了格瓦斯.饭后剩余500 cm3的格瓦斯没喝完，我倒入了底面积为60 cm2的圆柱形水杯（高20 cm）中带走，杯中格瓦斯的高度达到_______.

若把体积为V的格瓦斯倒入底面积为S的圆柱形水杯后，我又喝掉杯中体积为X的格瓦斯，此时其高度为_______.

师生活动：教师在创设的喀纳斯之旅的故事情境中，给出以上三个问题，学生独立思考，得到三个分数、三个新式子.体会并类比分数，写出新的式子表示问题中的数量关系，同时也为从分数到分式的抽象提供样例.

【设计意图】本环节尊重教材的编写意图，从实际问题引入，为了激发学生的学习兴趣，将教材中的“思考”及章前言中的部分问题纳入喀纳斯之旅的故事情境，主线是从分数到分式，符合学生从具体到抽象的认识事物的过程，渗透了建模的数学思想.

2.类比发现，形成概念

师生活动：先独立思考，再每三人或四人为一组讨论交流.教师巡视，对学生的讨论结果做到心中有数.学生以小组为单位汇报讨论结果，相互补充，得到以下结论.

不同点：分数的分子A与分母B都是整数，而这些式子中的分子A与分母B都是整式，并且分母B中含有字母.

教师明确这样的式子叫做分式，告诉学生从本节课开始学习第十五章“分式”，这节课的研究内容为从分数到分式，板书课题，概括分式概念.

【设计意图】分式概念的形成是本节课的难点，在此让学生类比分数，通过小组合作交流，教师巡视指导，逐步发现、揭示、归纳这类式子的本质属性.顺理成章地给出了课题——从分数到分式.学生经历概念抽象的主要活动，积累了概念抽象的活动经验，发展了数学抽象素养，实现了知识的迁移，突破了难点.

3.练习巩固，辨析概念

下列式子中，哪些是分式？哪些是整式？

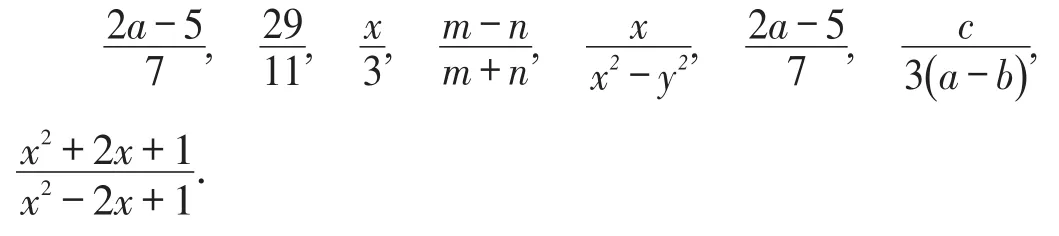
学生活动：学生自主思考，辨析分式与整式，并说明判断的理由.

4.合作探究，深化新知

完成下表.

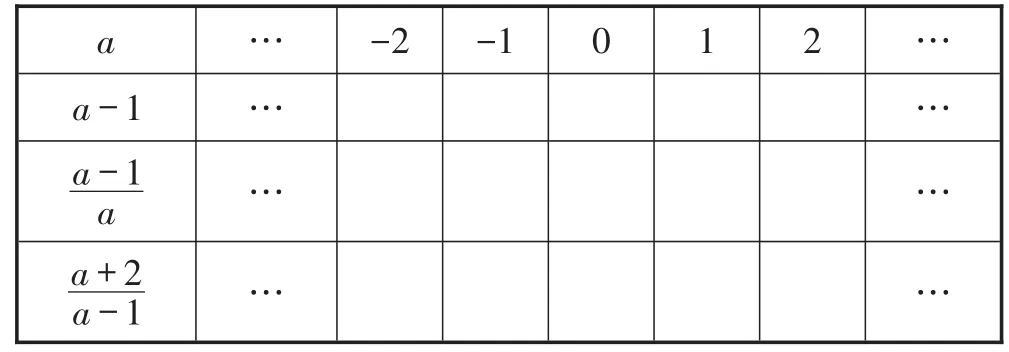
仔细观察表格中的数据，你发现了什么？

师生活动：学生独立填表、思考，然后小组讨论、交流发现的结论，教师巡视学生的交流情况.小组间相互补充，发现分式有意义和分式值为0的条件，以及分式比分数更具有一般性等结论.

【设计意图】设置填表探究这一开放性问题的意图是：（1）类比分数得到分式有意义和分式值为0的条件；（2）体会分式的值随字母取值不同而发生变化，渗透函数思想；（3）感受分数是分式中字母取某些值时的结果，分数与分式是特殊与一般的关系.

5.精讲精练，巩固新知

例 下列分式中的字母满足什么条件时分式有意义？

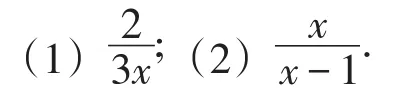
师生活动：学生分析题目要求，教师板书.

（2）要使分式有意义，分母x-1≠0，即x≠1.

【设计意图】教师规范板书，给学生做出示范.

练习：下列分式中的字母满足什么条件时分式有意义？

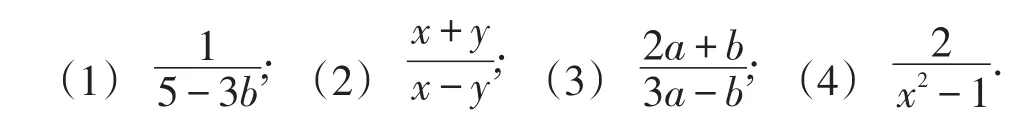
师生活动：让四位学生到黑板上解答，其余学生在练习本上解答，教师巡视指导.

【设计意图】学生对第（4）小题的解答可能会出现错误，让学生更正的同时教师强调了两解之间“且”的关系.通过讲练结合再次突出本节课的重点，完成教学目标.

6.拓展应用，能力提升

师生活动：学生填空.让学生发现问题，分式值为0，分子为0且分母不为0.

【设计意图】这道题中的分式为什么没有放到前面的表格中进行探究呢？表格中学生刚刚得到分式有意义的条件，立刻应用会增加难度，放在这里引发学生的认知冲突，从而完善或验证分式值为0的条件，让学生再次体会分式有意义的条件.

7.总结分享，梳理知识

同学们，这节课到这里已经接近了尾声，你有什么收获和困惑？大家可以畅所欲言.

师生活动：学生总结自己本节课的收获，提出困惑.教师播放视频进行总结.

【设计意图】学生分享收获，教师梳理知识，站在知识构建的平台上进行思维追溯和展望，起到“谷粒归仓”“画龙点睛”的作用，让学生感悟到数学知识的自然生长、学习经验的积累和学生的可持续发展.

8.布置作业，内化提高

（1）必做题：教材第133页习题15.1第1，2，3题.

【设计意图】分层作业旨在让不同的学生在数学上得到不同的发展.

五、目标检测设计

1.从布尔津县乘大巴车返回乌鲁木齐市，总路程为688千米，正常情况车速为b千米/时，由于返回时下雨，大巴车每小时比正常情况少行驶10千米，则到达乌鲁木齐市需要的时间为______.

【设计意图】考查学生根据实际情境列出分式的能力.

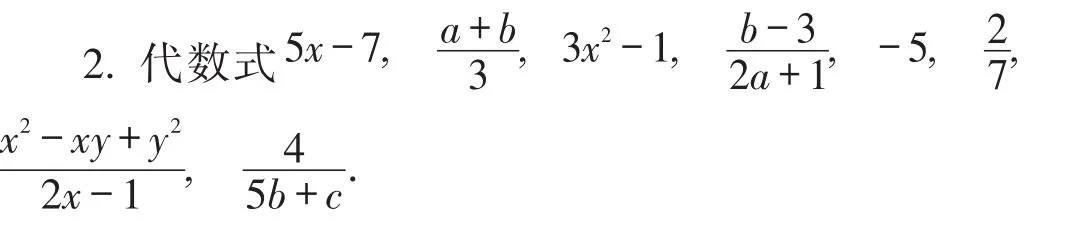
其中，分式有________；整式有________.

【设计意图】考查学生对分式概念的了解情况.

【设计意图】考查学生对分式有意义条件的理解情况.

六、教学反思

为了让教学内容生动有趣，将要得出的三个分数、三个分式纳入喀纳斯之旅的故事情境中，达到了从分数到分式的自然过渡，但是故事情节稍显牵强.

《义务教育数学课程标准（2011年版）》指出，列代数式表示数量关系是初中数学教学中非常重要的任务之一.因此，在教学中要充分尊重教材的编写意图，从实际问题引入，并用字母表示数，让学生列式得到足够多样的分式，感受从具体到抽象的认识事物的过程.通过学生活动类比分数，抽丝剥茧，得到分式的特点，从而抽象分式概念，符合学生的认知规律，培养了学生数学抽象的素养.

表格的设计蕴含多个结论，主要是为了让学生得到分式有意义的条件，感受分数是分式中字母取某些值时的结果，分数与分式是特殊与一般的关系，顺便得到分式值为0的条件.通过表格中的分式，让学生得到分式值为0的前提是分式的分母不为0这一结论有困难，故设计了拓展应用.教学环节精心设计、尊重学生，顺应学生的思维，达到了数学知识的自然生长，这是每位数学教师不断追求的方向.

参考文献：

［1］吴增生.发展抽象素养视角下的分式概念教学实践研究［J］.中国数学教育（初中版），2017（7/8）：3-7.

［2］罗增儒.核心素养与课堂研修（续）［J］.中学数学教学参考（中旬），2017（9）：2-5.