“正方形”教学设计

杨飞云

（河南省新乡市第二十二中学）

一、内容和内容解析

1.内容

正方形的定义、性质、判定，以及正方形、菱形、矩形、平行四边形之间的关系.

2.内容解析

“正方形”是人教版《义务教育教科书·数学》八年级下册（以下统称“教材”）第十八章第二节第三小节的内容.由于正方形既是特殊的矩形，又是特殊的菱形，因此正方形具有一般矩形和菱形的全部性质.作为一种特殊的矩形和菱形，正方形还具有一般矩形和菱形不具有的特殊性质.对正方形的研究突出体现了从一般到特殊的思路.从动态角度看，一个平行四边形在变形过程中，当一个角变为直角时，平行四边形就变形成矩形，当矩形的一组邻边相等时，矩形就变形成正方形.一个平行四边形在变形过程中，当一组邻边相等时，平行四边形就变形成菱形；当菱形的一个角变为直角时，菱形就变形成正方形.这是一个从一般到特殊的动态演变过程，它可以引导学生类比矩形和菱形的定义，得出正方形的定义，帮助学生理清正方形、菱形、矩形、平行四边形之间的关系.

基于以上分析，确定本节课的重点是正方形的定义，以及正方形与菱形、矩形的关系.

二、目标和目标解析

1.目标

（1）理解正方形的概念.

（2）掌握正方形的性质与判定，并能运用它们进行证明和计算.

（3）理解正方形、菱形、矩形、平行四边形之间的关系.

（4）培养主动探究的习惯和合作交流的意识，提高逻辑思维的能力.

2.目标解析

目标（1）的具体要求：明确正方形是特殊的矩形和菱形，能判定一个四边形是正方形.

目标（2）的具体要求：经历对正方形性质整理、归纳的过程，形成对正方形性质的完整认识；结合框架图分析得出正方形的判定，能用正方形的性质与判定进行推理与计算.

目标（3）的具体要求：结合框架图与集合图理清正方形、菱形、矩形、平行四边形之间的关系.

目标（4）的具体要求：通过动手操作、合作交流等活动培养学生主动探究的习惯，提高学生的逻辑思维能力.

三、教学问题诊断分析

从学生的学习过程来看，正方形在生活中广泛存在，因此学生从小就有对正方形的整体感知.在小学学习中，学生已经初步认识正方形的四条边都相等，四个角都是直角.这些都是在直观感知基础上的归纳认识，为本节课的学习奠定了一定的基础.要想掌握正方形的性质与判定，还需要理清正方形与菱形、矩形、平行四边形的关系.虽然学生已经学习了平行四边形、矩形、菱形，但是学生在理清正方形与它们之间的关系时仍有一定的困难.基于以上分析，确定本节课的难点是正方形的判定及正方形与菱形、矩形的关系.

四、教学支持条件分析

掌握正方形的概念是学好本节课的关键.通过flash动画演示，让学生认真观察图形变化，类比矩形、菱形的定义，得出正方形的定义.

通过问题引导，结合框架图和定义，理清正方形、菱形、矩形、平行四边形之间的关系，从而引导学生归纳出正方形的性质和判定.

通过学生活动：拼一拼、画一画、折一折，激发学生的学习兴趣，巩固正方形的判定.

五、教学过程设计

1.创设情境，引入新课

问题1：老师买了一条漂亮的丝巾，它是什么形状的？有哪些方法可以说明它是正方形？

师生活动：学生根据自己的直观认识，可以猜想出丝巾的形状是正方形，但是具体要如何判定，学生不一定清楚.因此，教师提出问题，激发学生的学习兴趣.

【设计意图】通过生活中的实例引入本节课，使学生感受到数学来源于生活.

2.探究新知，解决问题

问题2：类比矩形和菱形的定义，你能说说什么叫正方形吗？

师生活动：学生认真观察动画演示，教师引导学生类比矩形和菱形的定义给出正方形的定义.

追问：正方形是矩形吗？是菱形吗？为什么？

师生活动：学生通过小组讨论，结合正方形的定义，得出正方形既是矩形，又是菱形，教师认真倾听学生的发言，给予肯定与鼓励.

【设计意图】通过小组讨论，使学生清楚正方形既是矩形，又是菱形.

问题3：正方形有哪些性质呢？

师生活动：引导学生归纳正方形的性质，并用符号语言表示出来.

追问1：正方形的两条对角线把正方形分成的四个三角形的形状有什么特点？它们之间又有什么关系？为什么？

追问2：图中还有其他的等腰直角三角形吗？图中共有多少个等腰直角三角形？

师生活动：学生回答问题，教师给予肯定并得出结论.

【设计意图】梳理正方形的性质，并应用正方形的性质解决相关的问题.

问题4：如何判定一个四边形是正方形呢？

师生活动：教师设置一系列问题，启发学生思考.学生利用定义，结合框架图思考分析，完善框架图，并归纳出既是矩形，又是菱形的四边形是正方形.

追问：下列说法是否正确？为什么？

（1）四条边都相等的四边形是正方形.

（2）对角线互相垂直且相等的四边形是正方形.

（3）对角线互相垂直且相等的平行四边形是正方形.

（4）对角线相等的菱形是正方形.

学生活动：以小组为单位，利用手中的学具做出正方形（拼一拼、画一画、折一折），并说明理由.

【设计意图】通过合情推理得出正方形的判定方法，借助学生动手操作、合作交流，巩固正方形的判定方法，培养学生主动探究的习惯，提高学生的逻辑思维能力.

问题5：正方形、菱形、矩形、平行四边形之间有什么关系呢？

师生活动：教师引导学生结合框架图与集合图理清正方形、菱形、矩形、平行四边形之间的关系.

【设计意图】帮助学生结合框架图与集合图理清正方形、菱形、矩形、平行四边形之间的关系，从而突破难点.

3.当堂检测，巩固新知

（1）当堂检测.

①正方形具有而菱形不具有的性质是（ ）.

（A）四条边都相等

（B）对角线相等

（C）对角线平分一组对角

（D）对角线垂直且互相平分

②如图1，正方形ABCD的对角线AC，BD相交于点O，且AB=2 cm，则OA的长是（ ）.

（A）2 cm （B）2 2 cm

（C） 2 cm （D）1 cm

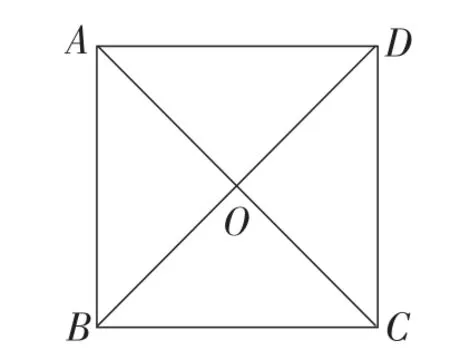
图1

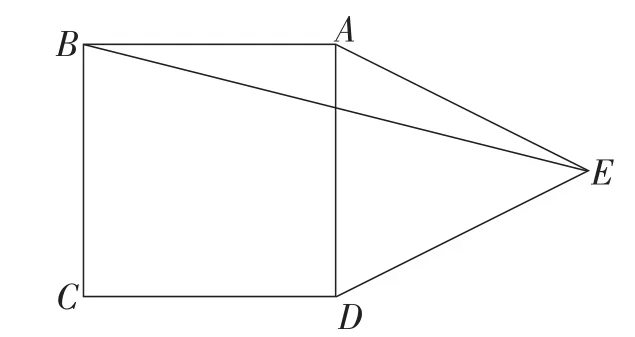
图2

③如图2，在正方形ABCD的外侧，作等边三角形ADE，连接BE，则∠AEB的度数为（ ）.

（A）10° （B）15°

（C）20° （D）12.5°

④如图3，在四边形ABCD中，对角线AC，BD相交于点O，下列条件中不能判定这个四边形是正方形的是（ ）.

图3

（A）AB∥CD，AB=CD，AB=BC，∠ABC=90°

（B）∠BAD=∠ABC=∠BCD=∠ADC，AD=AB

（C）AO=BO=CO=DO，AC⊥BD

（D）AO=CO，BO=DO，AB=BC

⑤已知四边形ABCD中，∠A=∠B=∠C=90°，添加一个适当的条件________________（填一个即可），使四边形ABCD为正方形.

（2）解决问题.

问题：你能帮老师证明这条丝巾的形状是正方形吗？你的依据是什么？

师生活动：学生当堂练习，动手操作，教师评价反馈.

【设计意图】巩固本节课所学知识，解决实际问题，使学生感受到数学来源于生活，又应用于生活.

4.畅所欲言，盘点收获

通过本节课的学习，你学到了哪些知识？掌握了哪些解决问题的方法？

师生活动：教师引导学生梳理本节课所学的知识，并对学生的表现给予总体评价.

【设计意图】培养学生的归纳、概括能力，鼓励学生养成良好的学习习惯.

5.布置作业，拓展提升

必做题：教材习题18.2第13，15题.

选做题：如图4，E是正方形ABCD的对角线BD上的一点，且EF⊥BC，EG⊥CD，垂足分别是点F，G.求证：AE=FG.

综合实践：用矩形纸片剪出正方形，你有哪些方法？

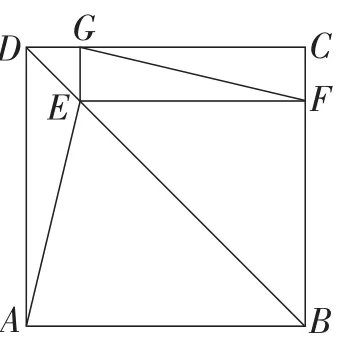
图4

【设计意图】分层布置作业，使不同的学生得到不同的发展.

6.板书设计

板书设计如图5所示.

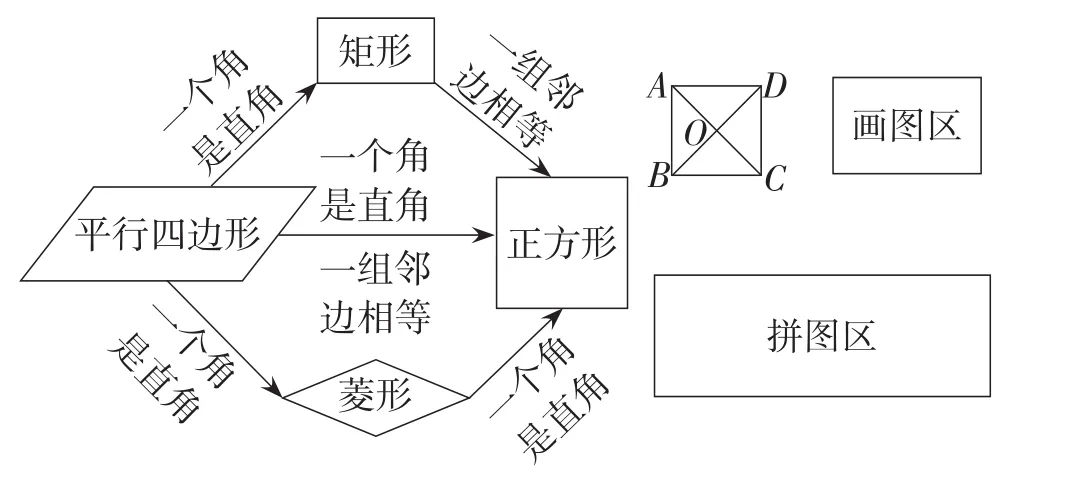
图5

【设计意图】突出本节课的重、难点，有利于梳理所学知识，构建知识体系.

六、教学反思

笔者通过深度挖掘教材，精心设计教学环节和内容，巧妙地运用学生活动，突出了重点，突破了难点，使学生循序渐进地学习了新知，基本达到了课前的预设，但也有少许的遗憾，现就本节课谈谈自己的一点看法，希望能够给大家提供一些借鉴之处.

对于本节课的教学，笔者在以下几个方面做出了努力.

1.教学目标明确具体，教学设计科学合理

教学目标是预期的学生学习结果，是设计教学过程、选择教学方法和安排师生活动方式的依据，是教学结果测量和评价的依据.清晰而具体化的目标能够有效地指导学生的数学学习.本节课的教学目标有两个：一是理解正方形的概念，以及正方形、菱形、矩形、平行四边形之间的关系；二是掌握正方形的性质和判定，并能运用它们进行证明和计算.其中理解正方形的定义是学好本节课的关键，笔者的教学设计正是抓住了这个关键.首先，通过动画演示使学生直观感知正方形的形成过程；其次，运用类比的方法，引导学生得出正方形的定义.无论是正方形的性质，还是判定，以及正方形、菱形、矩形、平行四边形之间的关系，都是围绕正方形的定义展开，使得问题迎刃而解.

2.注重发展学生的应用意识

应用意识有两个方面的含义：一方面，有意识地利用数学的概念、原理和方法解释现实世界中的现象，解决现实世界中的问题；另一方面，认识到现实生活中蕴含着大量与数量和图形有关的问题，这些问题可以抽象成数学问题，用数学的方法予以解决.本节课从实际生活情境出发，以购买的丝巾是否为正方形引入课题，体现了数学来源于生活，在学完新课之后，又让学生自己动手检验丝巾是否为正方形？做到首尾呼应，同时培养了学生应用数学的意识.

3.巩固正方形的判定，创新教学方式

在学习正方形的判定之后，教师打破传统的做习题来巩固所学内容的做法，通过让学生拼一拼、画一画、折一折的创新活动，积极思考、说理论证，不仅巩固了正方形的判定方法，而且极大地调动了学生学习的积极性，提高了学生的逻辑思维能力、动手操作能力和语言表达能力，学生在活动中的表现也给笔者带来了很多惊喜.

4.以问题促思考，以思考促发展

数学是思维的体操，问题被认为是数学的心脏.在数学课堂教学中，通过创设有效的问题情境，引导学生主动地参与到课堂活动中去，只要在课堂上学生一直能保持这种好奇心，全身心地投入到学习中，就能激发学生的学习兴趣和良好的思维习惯.本节课以问题为主线，问题设计涵盖本节课的核心内容，有明确的指向性，容易引发学生思考，并从中理解概念，领悟数学思想方法.例如，在开始时以教师买的丝巾是否为正方形引入新课；紧接着让学生观察动画演示，回答“类比矩形、菱形的定义，你能说说什么是正方形吗？”的问题，学生回答完之后，教师继续追问“正方形是矩形吗？正方形是菱形吗？为什么？”，这些问题的提出环环相扣，为学生自己总结出正方形的性质奠定了基础.

当然，通过教学与课后反思，笔者认为本节课还是存在一些问题的.

首先，由于“正方形”这一节课是八年级下学期的内容，录制教学课的时候八年级的学生还在学习八年级上册的内容，因此只能用九年级的学生，所以既要借班上课，又要学生把已学内容当做新授课来上.虽然笔者在上课之前会去了解学生，但是未必了解的那么多、那么深.而讲授这节课的时候，笔者只是根据《义务教育数学课程标准（2011年版）》来设计教学内容，实际上，通过教学可以发现，所借班级的学生学习情况比较好，如果在设计题目的时候，难度再大一些，是不是就不会导致生成问题少了呢？其次，在课堂上进行提问的时候，笔者关注更多的是举手的学生，至于什么样的问题让什么样的学生回答，学生能够回答到什么样的水平，心里真的没底.因此就导致对于不爱发言的学生和中等生，以及学困生的关注度不够，提问不够普及，这也是笔者在今后教学中需要改进的地方.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.