在探究过程中学会思考——对“勾股定理”一课的认识

綦春霞

（北京师范大学教育学部）

作为图形与几何的重要内容，勾股定理对于学生思维能力的培养起着非常重要的作用.执教教师的“勾股定理”一课，在设计中围绕着《义务教育数学课程标准（2011年版）》（以下简称《标准》）中“探索勾股定理及其逆定理，并能运用它们解决一些简单的实际问题”的要求，给学生思考、探究和发现勾股定理结论提供了机会.执教教师的这节教学设计有如下三个特点.

一、精准设计教学目标，并在教学中得以很好的贯彻

执教教师所讲授的是人教版《义务教育教科书·数学》八年级下册“勾股定理”（第1课时），根据教材的安排，将该节的目标确定为：（1）经历勾股定理的探究、证明过程.了解关于勾股定理的文化历史背景，通过对我国古代研究勾股定理的成就的介绍，培养学生的民族自豪感.（2）能用勾股定理解决一些简单问题.

在实际教学中，执教教师把教学重点放在了探索勾股定理上.本节课中一共用了28分钟的时间，带领学生从多种角度感受并经历勾股定理的探究、证明过程，了解关于勾股定理的文化历史背景，并通过对我国古代研究勾股定理的成就的介绍，培养学生的民族自豪感.而在10分钟左右的时间内，带领学生对勾股定理的简单应用进行练习巩固，通过学生的课堂表达反馈，我们发现学生掌握了该定理的运用.因此，本节课重点的把握十分清晰，详略得当.

二、教学过程环环相扣，体现定理探究的全过程

在整个教学过程中，从引入，到定理猜想、定理验证、定理应用各个环节自然连贯，上下流畅，体现了勾股定理的发展过程.

在引入阶段，执教教师联系旧知，直接引入要研究的主题，使得引入能够直奔主题.

在定理的猜想阶段，通过从实际情境到数学问题，从具体到一般化的抽象过程，逐步引导学生形成猜想.从基于毕达哥拉斯地砖问题（现实问题）入手，让学生通过对等腰直角三角形（边长分别为1和2）三边面积规律的探究，用同样的方法体会一般直角三角形（边长为2，3和边长为a和b）的三边面积规律，进而猜想出定理.

在定理验证阶段，通过切割和面积恒等法对勾股定理进行验证.进一步让学生归纳还有没有其他的验证方法，提升了学生数学思维能力.

最后结合具体例子，在带领学生体会勾股定理的应用，以及游览数学史长廊的过程中，激发学生的民族自豪感.

整个教学流程环环紧扣，主题明确，始终围绕着勾股定理的探索过程进行，突出是学生探究的方法和过程性的体验.

三、充分利用图形直观，发现、验证勾股定理

图形作为一种直观，在学生理解代数表达式中起到非常重要的作用.如果用拼图构造勾股定理，那么学生就会较为深刻地掌握这个定理，就如同学生用“24点游戏”能更好地理解有理数混合运算一样.赫布斯特认为，欲令学生参与合理猜想，画图、拼图起着重要的作用，因为操作的过程中产生了假设的对象，学生可以做出猜想，并证明猜想.

构图本身就是推理的一部分，也是发现和验证定理的重要手段.学生将外显的动手操作内化为有逻辑的思维活动，那么就成功实现了由直观到抽象的转变.在执教教师的课堂上，我们看到学生能够利用切割法和面积恒等法验证勾股定理的思路（图1、图2和图3）.能用拼图构造的方式证明勾股定理，说明学生深刻掌握了这个定理及其生成过程，这是本节课最大的成功.

图1

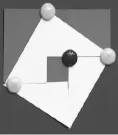
图2

图3

正是基于学生的动手操作，这为转化为一般化的图示说明提供了基础.尤其是赵爽弦图本身就是不太容易想到的方法，教师让学生通过拼图（图4～图8），有效地克服了难点，同时也为向一般化过渡提供了基础.

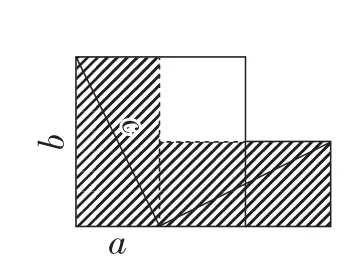
图4

图5

图6

图7

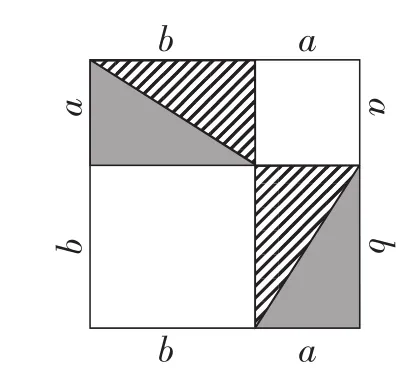
图8

此外，本节课还把探究延展到了课后.在教学结束时，教师提出了由直角三角形三边向外作半圆、正多边形，面积之间等量关系是否存在的问题，这些问题会激发学生进行持续性探索.

总的来讲，执教教师对此课的教学符合《标准》的要求，关注了学生的探索过程、思考过程，注重培养学生的推理能力.教师采用多媒体等方式，帮助学生去理解定理.整节课详略得当，活动设置合理，学生课堂参与度高，课堂上生成精彩，是一节非常优秀的示范课.但是教学是一门遗憾的艺术，本节课有两个方面需要后续思考.

（1）在引入环节，执教教师强调了我们可以从边的角度去研究直角三角形，但是为什么要通过平方的角度去研究呢？我们该如何实现从边长到面积的自然过渡呢？这仍然是该课题难以解决的问题.

（2）在小结部分，执教教师带领学生从数学文化、数学史的角度去总结勾股定理，设计十分巧妙、深刻.如果可以让学生提前查阅资料，并用讲故事的形式进行讲解，效果可能会更好.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.