“折纸做60°，30°，15°角”教学设计

李 倩

（四川省自贡市解放路中学）

一、内容和内容解析

1.内容

折纸做60°，30°，15°的角.

2.内容解析

本节内容是教材在三角形、轴对称、四边形、尺规作图等知识的基础上安排的一次综合与实践活动.教学重点是用矩形纸片折30°角和折叠问题的探究.学生通过折纸做角活动，既可以巩固再认已学知识，深化知识的理解与运用，又可以加强数学与生活的联系，积累活动经验，培养学生的应用能力、实践能力和元认知能力，为后续知识的学习和数学实践活动奠定认知基础.此外，本节教学内容蕴含了丰富的文化价值资源，有利于培养学生学习数学的兴趣和爱家乡、爱祖国的情感.

二、目标和目标解析

1.目标

（1）学生能掌握折60°，30°，15°角的方法；在实践操作中积累活动经验，提高动脑、动手能力.

（2）通过折叠探究活动，培养学生分析问题和解决问题的能力.

（3）通过折纸做角的实践操作活动，培养学生爱家乡、爱祖国的情感.

2.目标解析

达成目标（1）的标志是：首先，学生能运用“在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角是30°”和轴对称性质、勾股定理等知识，设计出用矩形纸片折30°角的方案；其次，进行实践操作折出30°角；最后，能利用角的倍分关系顺利折出15°，60°，120°等相关的角.

达成目标（2）的标志是：通过对折纸做角过程的反思再认，能理解对折纸片（折叠）的实质是轴对称，重合点的连线被折痕垂直平分，并能运用对称原理进行数学中折叠问题的一般推理和计算.

达成目标（3）的标志是：通过把自贡的地方剪纸文化与折纸紧密结合，学生表露出对家乡——自贡剪纸艺术的惊叹和赞赏，洋溢出对家乡、祖国的热爱之情，激发学生学习数学的兴趣和为传承祖国优秀文化遗产而努力学习的热情.

三、教学问题诊断分析

折纸做30°角，是在不使用任何作图工具的前提下，开展的一项数学实践活动，在抽象概括能力和实践操作技能方面都比尺规作图难度大.它要求学生具有一定的思维能力、推理能力和运算能力，并能够运用数形结合、转化、建模等数学思想方法解决问题；而且要求学生做到学用结合、手脑结合.此外，笔者所教班级少数学生因基础不扎实，动手能力较差，要完成目标任务有一定困难.

四、教学支持条件分析

虽然折纸做角难度较大，但是它和尺规作图的分析方法有相似之处，这对折纸做角的思维活动有启迪作用.另外，学生已经学习了三角形、勾股定理、轴对称性质、四边形、尺规作图等与活动相关的知识，有一定的推理和运算能力，并且在前面的数学实践活动中，积累了一些活动经验，可为本节数学活动提供认知支持条件.笔者所在学校开展的“学、究、讲、用”的课堂教学改革实验，较好地解决了教与学的二元矛盾.通过教师的导学，多数学生能积极主动地参与自主探究、合作探讨、展示交流等学习活动，这可为本节数学活动提供学习主体的能动支持条件.

教师在教学活动中采用微课导学等现代信息技术手段，把折叠问题从平面与立体、静态与动态进行对比分析，能增强教学的直观性，降低理解难度，提高学习效率，这可以为本节数学活动提供教学手段的媒体支持条件.

五、课前准备

多媒体课件、微课视频、矩形纸片、实物投影仪等.

六、教学过程设计

1.创设情境，导入新课

同学们，我们美丽的家乡自贡有着厚重的文化底蕴和丰富的地方文化元素，它不仅有闻名世界的“大三绝”，还有享誉中外的“小三绝”.下面请看视频.

学生观看自贡“大三绝”和“小三绝”的视频短片，感受“小三绝”中的剪纸与折纸做角的关系.

教师自然导入新课，并板书课题.

【设计意图】创设与教学内容密切相关的生活情境，把数学还原于生活，呈现数学与生活的联系，从数学的运用价值上，激发学生学习的兴趣和动力，为教学活动做情感铺垫.

2.实践活动，学用结合

活动1：将一张矩形纸片，不用任何工具，折出45°的角.

师生活动：学生思考折叠方法，进行折角活动，并交流展示.教师播放折45°角的动画课件.

活动2：（方法1）给你一张矩形纸片，不使用任何作图工具，折出30°的角.

师生活动：教师出示活动2的课件，启发学生联想与角相关的数学知识，引导学生设计折叠方案，组织开展折叠活动，并巡视指导，针对折叠活动的具体情况及时进行点拨指导.学生在教师的启发下能联想到“在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°.”学生进行小组交流活动，展示交流折叠成果或折叠困惑.教师播放折30°角的动画课件，组织学生自学教材.

【设计意图】通过类比的思想方法，促进探究活动由易到难的过渡迁移，减缓折叠30°角的难度.通过成功促进策略，激励学生树立攻坚克难的信心.

（方法2）启发学生还有没有其他方法可以折出30°的角.

师生活动：请学生折叠，但是没有折出来.在学生遇到困难时，启发学生“由方法1想到，在直角三角形中，一条直角边为1，另一条直角边为 3，同样可以得到30°的角”.为学生播放用尺规作图法画线段 3的微课视频，再启发学生思考折叠方法.学生进行小组交流活动，观看教师制作的动画课件，领会折角步骤，说明利用角的倍分关系可以折出15°，60°，120°等角.

【设计意图】通过一题多法，培养学生思维的灵活性、敏捷性和创造性.

3.实践再认，原理运用

小结：引导学生反思折纸做角的实质（折叠的实质是轴对称），并结合课件进行说明.

探究1：实践与运用.

第一次折叠：将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图1（1））；

第二次折叠：再沿着过点E的直线折叠，使点D落在BE上的点D′处，折痕为EG（如图1（2））；再展平纸片（如图1（3）），求图1（3）中∠α的大小.

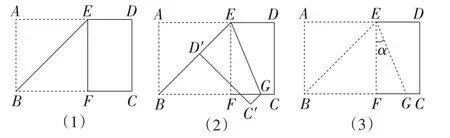
图1

课件做一次动态展示.

解：由图1（1）可知，四边形ABFE是正方形，且∠AEB=45°，得∠BED=135°.

又由图1（2）知，∠BEG= ∠DEG.

得∠DEG=67.5°.

所以∠α=∠FED-∠DEG=90°-67.5°=22.5°.

探究2：如图2，在矩形纸片ABCD中，AB=8，将纸片折叠，使顶点B落在边AD上的点E处，折痕的一端点G在边BC上，BG=10,当折痕的另一端点F在AB边上时，试求△EFG的面积.

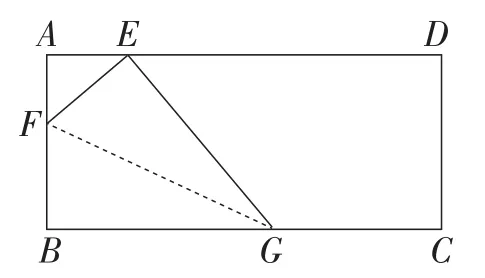
图2

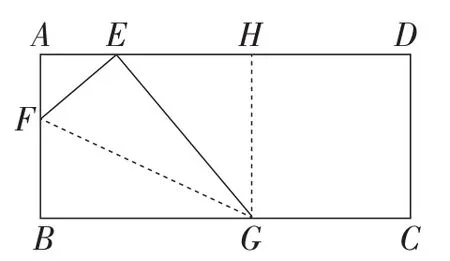
图3

课件动态展示，闪烁△EFG的面积.

解：如图3，过点G作GH⊥AD，垂足为点H.

因为四边形ABCD是矩形，

所以四边形ABGH为矩形，AH=BG=10.

由折叠，得EG=BG=10，EF=BF.

在Rt△EGH中，EG2=HG2+EH2，即102=82+EH2.

所以EH=6，AE=10-6=4，AF=8-BF.

设BF=x，则EF=x，AF=8-x.

在Rt△AEF中，EF2=AF2+AE2，即x2=(8 -x)2+42.解得x=5.

【设计意图】创造性地处理教材，促进教材使用的校本化.强化对学生思维能力和思想方法等核心素养的培养.

4.及时练习，巩固提升

练习：（1）如图4，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，求∠AEF的度数.

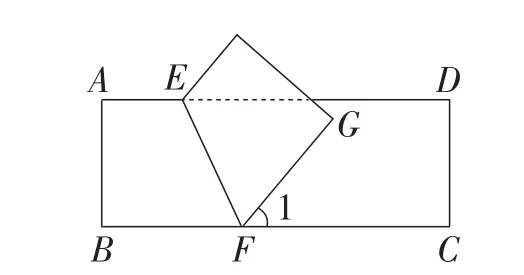
图4

解：由两部分对折可知∠BFE=∠GFE.因为∠1=50°，所以∠BFE=∠GFE=65°.所以∠AEF=115°.

（2）将矩形纸片ABCD按如图5所示的方式折叠，得到如图6所示的菱形AECF.若AB=3，则BC的长为多少？

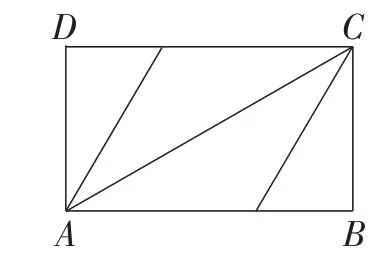
图5

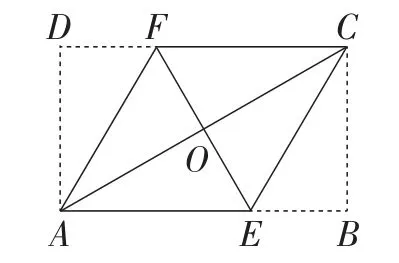
图6

设BC=x，则AC=2x.

在Rt△ABC中，由勾股定理得x2+32=(2 x)2.

【设计意图】强化折叠原理的应用，培养学生提出问题、分析问题和解决问题的能力，渗透对转化、建模等数学思想方法的教学.

5.课堂总结，知识重构

回顾折纸的基本步骤，即明晰要求—联想知识—制定方案—实践操作—推理验证.

必做题：（1）用矩形纸片折15°，75°的角.

（2）将一张矩形纸片折叠成如图7所示的形状，则∠ABC的度数为（ ）.

（A）70° （B）66° （C）73° （D）80°

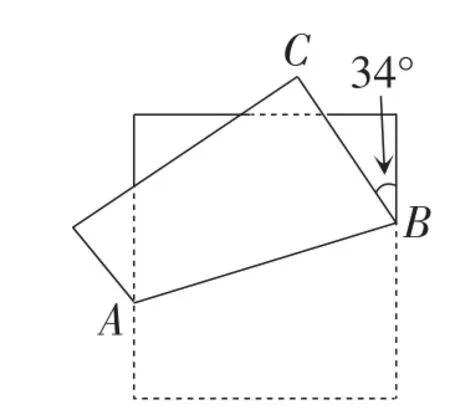
图7

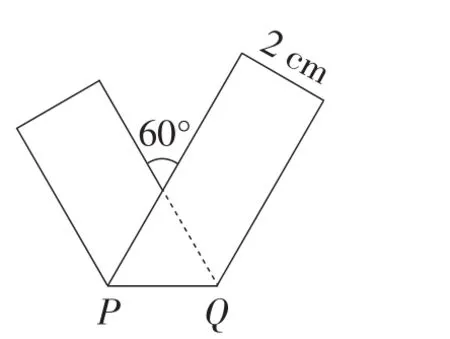
图8

（3）将宽为2 cm的长方形纸条折叠成如图8所示的形状，那么折痕PQ的长是（ ）.

（4）以学习小组为单位，设计制作一幅剪纸画.

选做题：如图9，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE，并延长交AD于点F.

①求证：四边形BCFD是平行四边形；

②如图10，将四边形ACBD折叠，使点D与点C重合，HK为折痕，求的值.

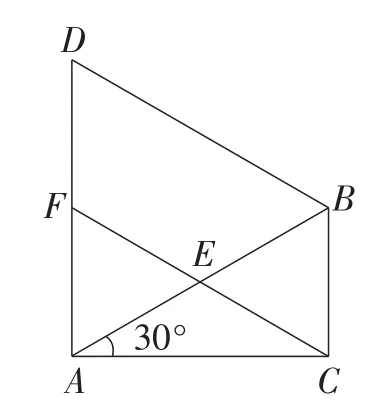
图9

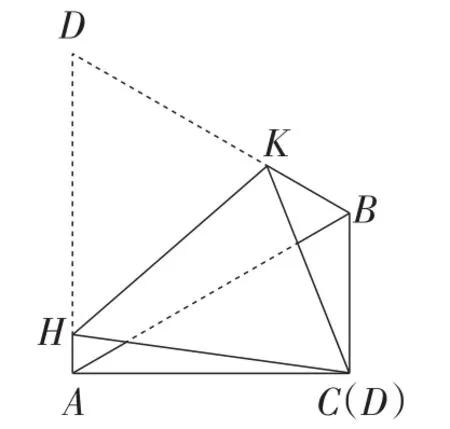
图10

板书设计略.

七、教学反思

“折纸做60°，30°，15°的角”选自人教版《义务教育教科书·数学》八年级下册中的数学活动，属于义务教育阶段数学内容中“综合与实践”的部分.该教学设计和教学活动的组织突出了科学性、实践性和创新性等特点，主要体现在以下几个方面.

1.教学内容分析到位，挖掘深入

教师能够从知识系统的高度，理顺所教知识与上下位知识的联系，能紧密把握教学内容与学生知识经验和生活经验的关系，准确理解和掌握本节教学内容的实践性、运用性和探究性的特点；特别是把自贡的剪纸文化与折角活动紧密联系起来，较好地挖掘了教学内容所蕴含的文化价值资源.

2.教学目标符合实际，达成度高

教师对教学目标的制定，充分结合了《义务教育数学课程标准（2011年版）》的要求、教材特点和学生实际，目标紧扣具体内容，在知识与能力、过程与方法、情感态度与价值观方面，把结果性目标和过程性目标表述的具体、清楚、准确；通过实施有效的教学手段和方法达到预设的目标要求.

3.教学结构设计合理，过程流畅

在教学设计上根据内容由浅入深的特点，教学环节层层递进，内容环环相扣，过渡自然、流畅，逻辑性强，遵循了循序渐进的教学原则.

4.教学活动遵循规律，课改意识强

教师在组织学生折角活动中，启发学生运用已有知识和经验开展折叠活动，又对实践活动进行理性的反思再认，从而抽象、概括出折叠的本质是轴对称，再引导学生运用这个原理进行数学的相关探究活动.整个探究活动着眼于学生的认知基础，遵循了“实践—认识—再实践—再认识”的认识规律.

在教学中，教师有机渗透了课改的理念，较好地处理了教与学的辩证关系，通过采用启发、引导、点拨、激励等导学方法，有效地组织学生开展实验、观察、猜想、计算、推理、验证等认知活动，培养了学生自主学习、合作学习和探究式学习的方法，营造了互动、互补、互进的学习氛围，极大地调动了学生学习的主动性和积极性.

5.课堂机制灵活，教学针对性强

采用提问、演练、展示、巡视、察言观色等多种方法捕捉教与学的反馈信息，并及时调控、调整教学方案，教学针对性、实效性强.

6.突出了数学本质特征，数学味浓

围绕目标要求设计了有价值的问题串，用以引导学生开展思维活动，培养了学生思维的灵活性和创造性，特别是在折角活动中，启发学生利用直角三角形的边角关系，把要折的30°角建构在特定长度的直角三角形中.又如在运用折叠原理进行探究活动时，引导学生把要求的线段、角建构在一个具体图形中，再制定解决方案，较好地渗透了数形结合、转化、建模等数学思想方法的培养.

7.媒体手段使用得当，教学效率高

利用现代信息技术辅助手段对本节教学难点从平面到立体、静态到动态进行对比分析，把抽象的折角过程演绎的直观易懂，提高了学生的学习兴趣和学习效率.

当然，教师在授课过程中也存在很多问题，如板书太简略，示范性不够强，不利于中等生和学困生对解题过程的理解.

参考文献：

［1］顾泠沅.数学思想方法［M］.北京：中央广播电视大学出版社，2004.