机械展开式超音速气动减速器模态分析
史明东,原梅妮,侯秀成,张佳庆,陈贺贺,何小晶
(1.中北大学 机电工程学院, 太原 030051; 2.晋西工业集团有限责任公司, 太原 030027)
传统的再/进入航天器气动构型都是刚性固定式结构,受运载火箭整流罩包络约束,极大地限制了航天器气动构型尺寸、质量及弹道系数[1]。可展开气动减速技术(SMDADT)以其独特的结构形式可以实现气动面在发射时收拢、再/进入时展开等功能,从而彻底克服了传统再/进入航天器受火箭包络约束的缺点[2-3]。SMDADT已成为第二代高效再/进入减速技术中最活跃的一个分支[4]。
气动减速器的结构动力分析是减速器系统设计中的一个重要环节。减速器动态响应计算、结构动稳定性分析以及结构与其他子系统的耦合干扰分析,往往都是以结构动态固有特性为基本依据[5]。因此,在减速器设计过程中首先需要对减速器结构进行模态分析,得到减速器的固有频率和振型,从而开展对减速器结构特性的优化设计。目前,国内外对机械展开式气动减速器的研究主要集中在气动特性分析和防热材料研制等方面[6-9],而减速器结构动力学分析尚无公开报道;而对于空间可展开结构的动力学研究方面,Ando等[10]对空间可展开天线的网面和背架进行了多体动力学分析和实验验证,并分析了模块数量变化时天线固有频率的变化趋势。张春等[11]采用牛顿—欧拉法对提出的径射状可展开结构进行了动力学建模。刘荣强等[12]分析了不同结构参数对构架式空间可展开天线背架的固有振动特性的影响规律,给出了提高其一阶模态的方法。
本研究基于Block Lanczos 方法对所建立的气动超音速减速器有限元模型进行模态求解,得到了结构的前6阶固有频率和振型,分析了固有频率的变化规律及振型的特点;该分析方法为展开式气动减速器的动力学研究及结构的优化设计提供了理论参考。
1 模态分析
振动模态分析用于求出结构自然频率和模态形状,也称固有频率和主振型。该分析的结果对于实际工程设计有关参数的选择及进一步动力分析都具有重要意义。
结构运动的有限元方程表达为如下矩阵形式
(1)
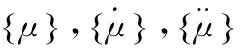
在式(1)中,令F(t)=0,即得到自由振动方程。在实际工程中,阻尼对结构固有频率和振型的影响不大,可忽略阻尼力,得到无阻尼自由振动方程;式(1)变为
(2)
设结构的自由振动为简谐振动,即位移为正弦函数:{μ}={φ}sin(ωt),代入式(2)得齐次方程:
([K]-ω2[M]){φ}={0}
(3)
解算即可得到结构的各阶固有频率ωi,以及对应振型{φ}i。
2 有限元模型的建立
所研究的气动减速器由支撑杆、连杆、中心支架,座圈,柔性蒙皮等零部件组成,其再入过程展开状态为类似伞状结构。利用三维建模软件建立减速器三维模型,通过接口格式导入ansys有限元软件进行模态分析。减速器模型如图1所示。
有限元模态分析预处理过程需要进行模型的材料定义,包括材料的弹性模量、泊松比、密度等。气动减速器零部件选用材料:中心支架、连杆、支撑杆、座圈为2A12铝合金;柔性蒙皮为TPS复合材料[6],材料特性如表1所示。

表1 计算用材料特性数据
边界条件的设置直接影响整个机构的振型和固有频率,其中定义柔性蒙皮与支撑杆、中心支架与座圈之间接触类型为boneded约束,支撑杆与连杆、连杆与中心支架、支撑杆与座圈通过销轴将各部件联接起来,销轴铰接采用如下处理方法:去除销轴,在销轴中心销建立外部节点,在外部节点和销轴孔内表面之间采用RBE2单元建立刚性区域,约束径向自由度,保留切向自由度[13]。在实际情况中减速器还与刚性防热头锥、固体发动机等部件与其相连接,它们对气动减速器的模态有一定的影响。 为了更准确地分析气动减速器的模态,将刚性防热头锥、固体发动机这2个质量较大的部件以质量单元的方式与相关部位刚性连接。系统模态特性是由减速器本身的结构特性和材料特性所决定的,和外载条件无关。对整个减速器不施加任何约束,进行自由模态分析。
在有限元软件中对模型进行网格划分,考虑到复杂结构对网格质量和计算结果都有很大影响,因此,在不影响计算精度的前提下,对减速器结构进行简化处理。并根据减速器各零部件的特点单独进行网格划分,对于减速器的支架、连杆、中心支架等采用实体单元(SOLID185)进行网格划分,柔性气动面采用2维壳单元(shell181)进行网格划分。最终节点为359421个,形成的单元总数为184828个,其中,板壳单元8971个,实体单元175857个,质量单元12个。有限元模型如图2所示。
3 模态分析的结果
利用Block Lanczos方法对所建立的气动超音速减速器有限元模型进行自由模态求解[14],得到了气动超音速减速器的各阶固有频率和各阶模态振型图。计算得减速器的前6阶固有频率及振型如表2所示,模态振型图如图3所示。从图3及表2可以看出,气动减速器的前3阶振型主要表现为整体的弯曲或扭转,但从第4阶振型起,开始出现局部杆件屈曲变形,局部振动增加,整个结构表现为整体与局部的复合振动,局部振动表现更为明显。也就是说减速器在低阶模态时表现为整体振动,高阶模态表现为局部振动。
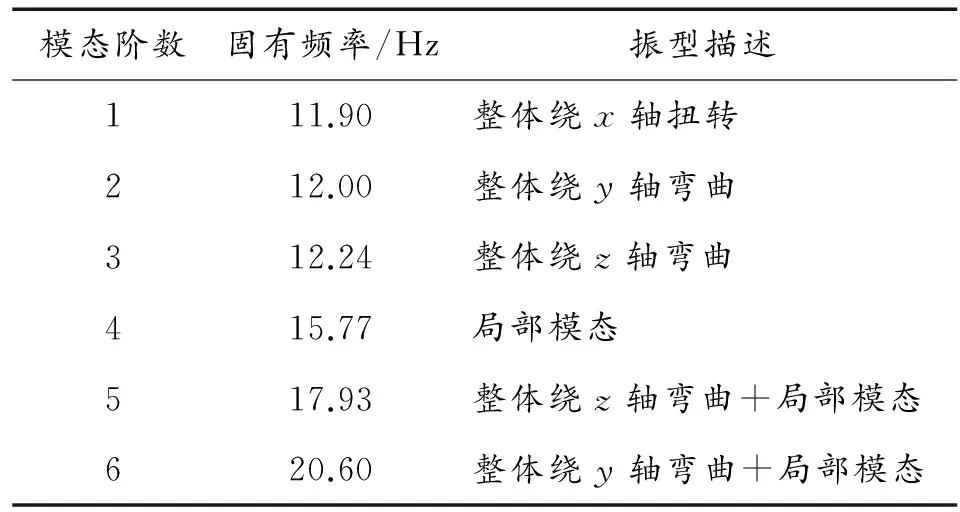
表2 减速器各阶固有频率及振型描述
由表2可以看出,气动减速器固有频率各阶数间比较密集,其前六阶固有振动频率范围在11.90~20.60 Hz之间,已知再入时任务载荷仓的第一阶固有频率为32 Hz,且30~50 Hz 为主要激振区,因而气动减速器的固有频率设计合理,满足使用要求。
4 结论
利用结构有限元分析软件ANSYS对可展开式超音速气动减速器的固有振动特性进行了分析,得到如下结论:
1) 在建立有限元模型时,在不影响计算精度的前提下,对几何模型做适当简化,可有效提高网格品质,也为后续计算节省时间。
2) 当振动频率较低时,气动减速器主要表现为整体振动; 当频率超过某一固有频率时,结构中开始出现局部杆件屈曲变形,整个结构表现为整体与局部的复合振动,局部振动表现更为明显。
3) 通过对对气动减速器前6阶固有频率与载荷仓激振频率的对比分析,表明气动减速器的固有频率设计合理,满足使用要求。该分析方法可为展开式气动减速器的动力学研究及结构的优化设计提供参考。
参考文献:
[1] 张鹏,李旭东,白良浩,等.半刚性机械展开式气动减速技术述评[J].航天返回与遥感,2016,37(1):1-9.
[2] 李爽,江秀强.火星进入减速器技术综述与展望[J].航空学报,2015,36(2):422-440.
[3] YOUNT B,ARNOLD J O,GAGE P,et al.Structures and Mechanisms Design Concepts for Adaptive Deployable Entry Placement Technology[C]//Aiaa Aerodynamic Decelerator Systems.2013.
[4] 张鹏,尚明友,李旭东,等.半刚性机械展开式气动减速技术机构特征研究[J].航天返回与遥感,2016,37(5):37-48.
[5] 张琪,刘莉.导弹等效密度有限元模型的模态分析[J].兵工学报,2008,29(11):1395-1399.
[6] CORSO J D,CHEATWOOD F,BRUCE W,et al.Advanced High-Temperature Flexible TPS for Inflatable Aerodynamic Decelerators[J].Aiaa Journal,2011.
[7] STERN E,BARNHARDT M,VENKATAPATHY E,et al.Investigation of transonic wake dynamics for mechanically deployable entry systems[C]//Aerospace Conference.IEEE,2012:1-10.
[8] SMITH B,YOUNT B,VENKATAPATHY E,et al.Progress in Payload Separation Risk Mitigation for a Deployable Venus Heat Shield[C]//Aiaa Aerodynamic Decelerator Systems.2013.
[9] VENKATAPATHY E,HAMM K,FERNANDEZ I,et al.Adaptive Deployable Entry and Placement Technology (ADEPT):A Feasibility Study for Human Missions to Mars[C]//Aiaa Aerodynamic Decelerator Systems Technology Conference and Seminar.2006.
[10] ANDO K,JIN M,SENBOKUYA Y.Analyses of cable-membrane structure combined with deployable truss[J].Computers & Structures,2000,74(1):21-39.
[11] 张春,王三民,袁茹.空间可展机构弹性动力学特性研究[J].机械科学与技术,2007,26(11):1479-1482.
[12] 刘荣强,田大可,邓宗全,等.构架式空间可展开天线背架的固有特性分析[C]//中国宇航学会深空探测技术专业委员会第7届学术年会论文集.哈尔滨,2010.
[13] 李发宗,童水光,王相兵.基于模态分析的液压挖掘机工作装置动态优化设计[J].农业机械学报,2014,45(4):28-36.
[14] 张琪.利用有限元和Lanczos法的细长弹体模态分析[J].弹箭与制导学报,2007,27(4):61-63.

