三角函数常见典型考题赏析

■翟新超

题型1:角的集合表示及象限角的判断

(1)利用终边相同的角的集合可以求适合某些条件的角,其方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k赋值求得所需角。(2)利用终边相同的角的集合S={β|β=2kπ+α,k∈Z}判断一个角β所在的象限时,只需把这个角写成[0,2π)范围内的一个角α与2π的整数倍的和,然后判断角α所在的象限。

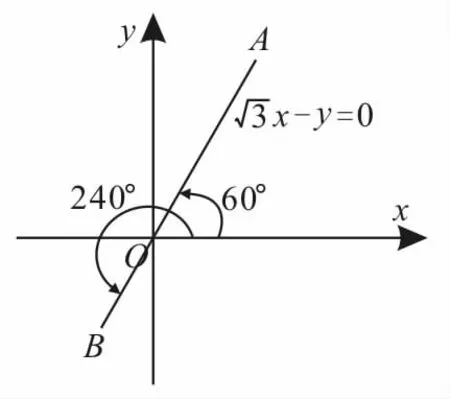
图1

在0°～360°范围内,终边落在射线OA上的角是60°,终边落在射线OB上的角是240°,所以以射线OA,OB为终边的角的集合分别为S1={β|β=60°+k·360°,k∈Z},S2={β|β=240°+k·360°,k∈Z}。

故角β的集合S=S1∪S2={β|β=60°+k·360°,k∈Z}∪{β|β=60°+180°+k·360°,k∈Z}={β|β=60°+2k·180°,k∈Z}∪{β|β=60°+(2k+1)·180°,k∈Z}={β|β=60°+k·180°,k∈Z}。

跟踪训练1:若α是第二象限的角,则下列结论一定成立的是( )。

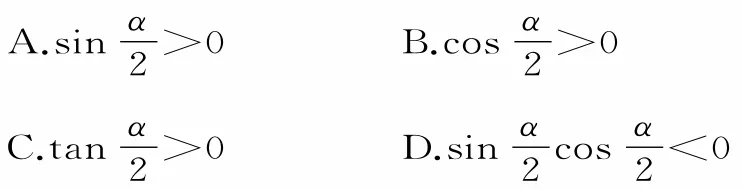
题型2:三角函数的取值符号的判断

熟练掌握三角函数在各个象限内的取值符号是学好三角函数的基础。可借助口诀“一全正,二正弦,三正切,四余弦”,来加深对三角函数取值符号的理解。

A.第一象限角 B.第二象限角

C.第三象限角 D.第四象限角

解:由sinαtanα＜0,可知sinα,tanα异号,则α为第二或第三象限角;

综上可知,α为第三象限角。应选C。

A.第一象限

B.第三象限

C.第一或第三象限

D.第二或第四象限

提示:因为sinα＞0,cosα＜0,所以α为第二象限角,即+2kπ＜α＜π+2kπ,k∈Z,+kπ,k∈Z。当k为偶数时,为第一象限角;当k为奇数时为第三象限角。应选C。

题型3:关于sinα，cosα的齐次式问题

形如asinα+bcosα和asin2α+bsinα·cosα+ccos2α的式子分别称为关于sinα,cosα的一次齐次式和二次齐次式,对涉及它们的三角变换问题通常可转化为正切来求解。

因为(cosα-sinα)2=1-2sinαcosα=

所以(sinα-cosα)2=1-2sinαcosα=

题型4:利用诱导公式化简与求值

三角函数的化简和求值问题,遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行三角函数名称的转化,以保证三角函数名称最少。

题型5:三角函数的定义域与值域

求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数图像来求解。求解三角函数的值域(最值)常见以下几种类型的题目:①形如y=asinx+bcosx+c的三角函数,可化为y=Asin(ωx+φ)+k的形式,再求值域(最值);②形如y=asin2x+bsinx+c的三角函数,可设sinx=t,化为关于t的二次函数求值域(最值);③形如y=asinxcosx+b(sinx±cosx)+c的三角函数,可设t=sinx±cosx,化为关于t的二次函数求值域(最值)。

故此函数的定义域为:

题型6:三角函数的奇偶性、周期性和对称性

求解三角函数的奇偶性和周期性问题时,一般先要进行三角恒等变换,把三角函数式化为一个角的一种三角函数,再根据函数奇偶性的概念、三角函数奇偶性规律、三角函数的周期公式求解。正、余弦函数的图像既是中心对称图形,又是轴对称图形,正切函数的图像只是中心对称图形,应熟记它们的对称轴和对称中心,并注意数形结合思想的应用。

例 6 已知函数f(x)=sin(ωx+φ)(ω＞0,|φ|＜)的 最 小 正 周 期 为4π,且f()=1,则函数f(x)图像的一个对称中心是( )。

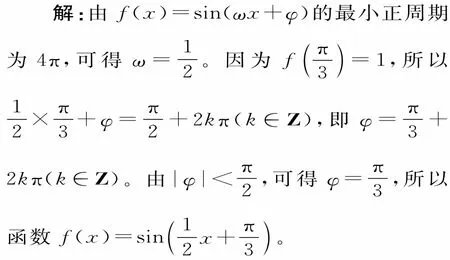
题型7:三角函数的单调性的应用

求形如y=Asin(ωx+φ)+k的单调区间时,只需把ωx+φ看作一个整体代入y=sinx的相应单调区间内即可。若ω为负数,则要先把ω化为正数再求解。

解:f(x)=sinωx(ω＞0)的图像过原点。

题型8:三角函数的图像变换

函数y=Asin(ωx+φ)(A＞0,ω＞0)的图像的两种作法:①五点法:主要是通过变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x值,通过列表,计算得出五点坐标,描点后得出图像。②图像变换法:主要途径有“先平移后伸缩”与“先伸缩后平移”。

例8 某同学用“五点法”画函数f(x)=Asin(ωx+φ),ω＞0,|φ|＜在某一个周期内的图像时,列表并填入了部分数据,如表1所示。

表1

(1)请将上表数据补充完整,并直接写出函数f(x)的解析式。

(2)将y=f(x)图像上所有点向左平行移动θ(θ＞0)个单位长度,得到y=g(x)的图像。若y=g(x)图像的一个对称中心为求θ的最小值。

(3)作出函数f(x)在长度为一个周期的闭区间上的图像。

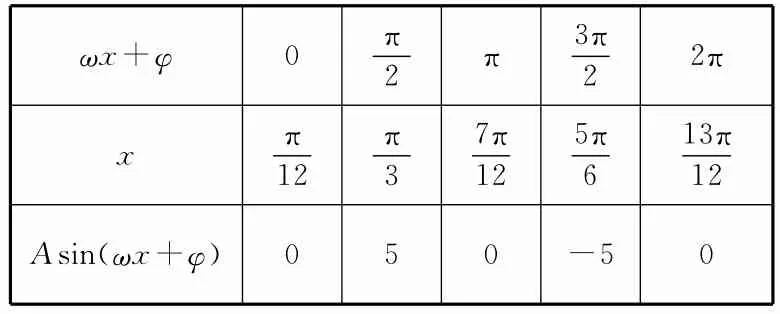
表2

由函数y=sinx图像的对称中心为(kπ,0),k∈Z,可令2x+2θ-=kπ,k∈Z,

(3)由表2可作出此函数在一个周期内的图像,如图2所示。

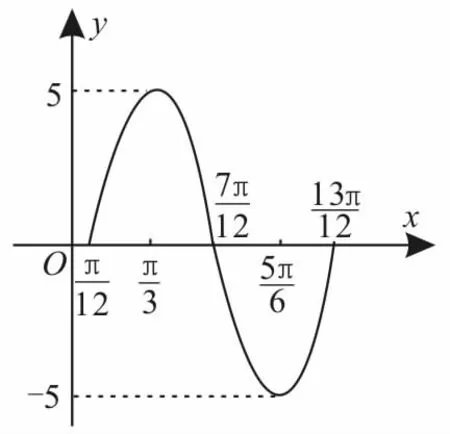
图2

跟踪训练8:函数f(x)=Asin(ωx+φ)(A＞0,ω＞0,|φ|＜)的图像如图3所示,为了得到f(x)的图像,则只需将函数g(x)=sin2x的图像( )。

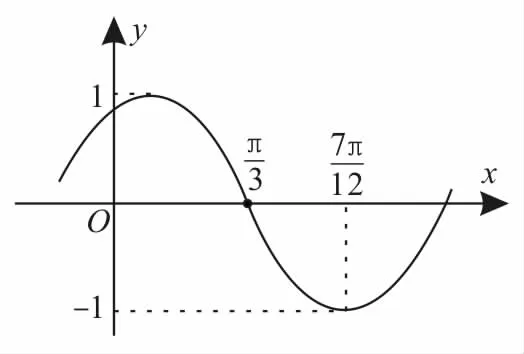
图3

题型9:求三角函数的解析式

求函数f(x)=Asin(ωx+φ)+B 的解析式的一般步骤:①由A=,B=,求A,B的值,其中M 为函数的最大值,m为函数的最小值。②由ω=π,求ω的值。③由图像上的一个已知点可求φ的值,或利用“五点法”中的对应点,也可求φ的值。

例 9 设函数f(x)=sin(ωx+φ)(ω＞0,0＜φ＜)的部分图像如图4所示,直线x=是它的一条对称轴,则函数f(x)的解析式为 。

图4

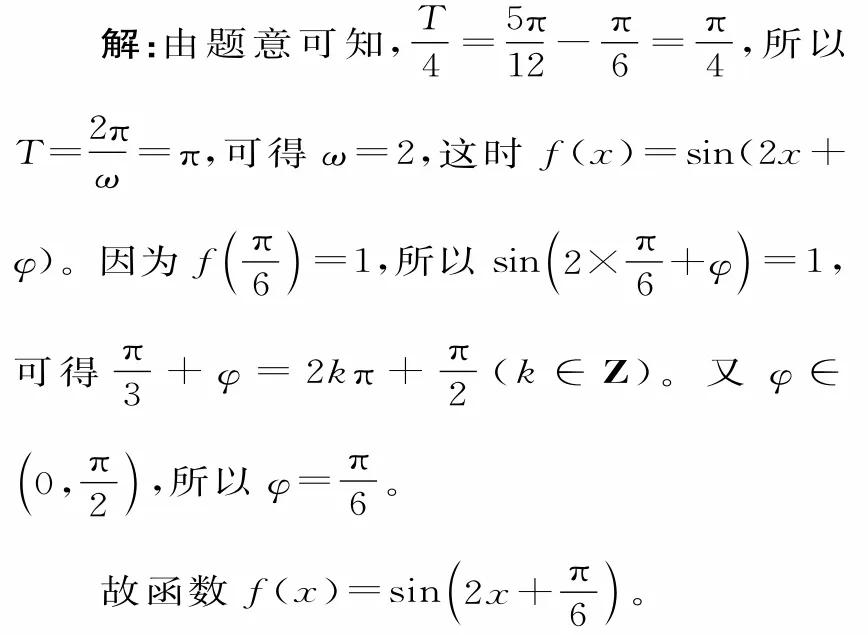
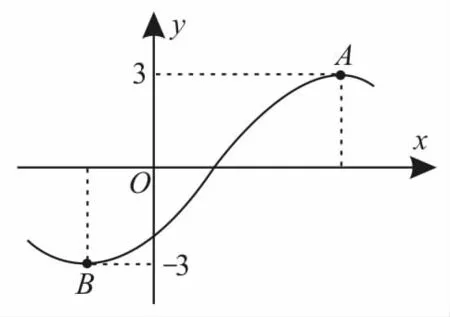
图5

A.1 B.2

C.3 D.4

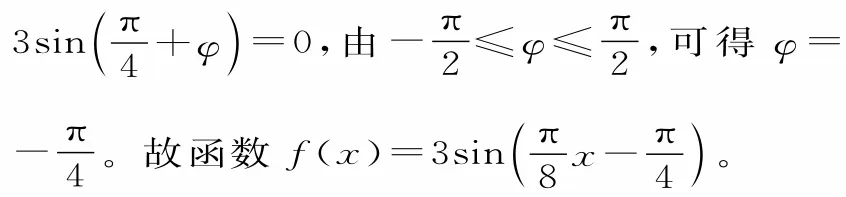
将函数f(x)的图像向右平移t(t＞0)个单位长度,所得的函数图像对应的函数解析

题型10:三角函数的图像与性质的综合应用

高考对三角函数的图像与性质的综合应用问题的考查主要有以下四种命题角度:①图像变换与函数性质。②恒等变换与函数性质。③三角函数性质与平面向量。④三角函数性质与解三角形。

(1)当f(x)为偶函数时,求φ的值。

跟踪训练10:下列函数同时具有性质“①最小正周期是π,②图像关于直线x=上是减函数”的是( )。