本期试卷参考答案与提示
编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

三角函数综合演练A卷参考答案与提示
一、选择题
1.C 提示:按顺时针方向旋转为负角,拨快10min所转过的角为圆周的,即为。 2.C 3.C 4.D 5.D 6.C 7.A 8.B 9.B 提示:由题意可得方程组则ω=2k+1,k∈Z,单调递增,在区间上单调递减,不满足上单调;若ω=9,则φ=单调递减。 10.C 11.C 12.D 13.D 14.A 15.B 16.B 提示:由已知得(sinθ-cosθ)2>1,即1-2sinθcosθ>1,sinθcosθ<0。又sinθ>cosθ,所以sinθ>0>cosθ,所以角θ的终边在第二象限。 17.B 提示:由f(x)=2sin(ωx+φ)对任意的x都有f(+x)=f(-x),知该函数的图像关于直线x=对称。在对称轴处对应的函数值为最大值或最小值。 18.A 提示:由19.B 20.B
21.D 22.A
二、填空题

三、解答题

31.提示:由f(x)的最小正周期为π,可得ω=2,这时f(x)=sin(2x+φ)。


三角函数综合演练B卷参考答案与提示
一、选择题
1.A 2.C 提示:设圆的半径为r,则其内接正三角形的边长为r,所以3r=αr,即α=。 3.A 4.A 提示:此函数的周期T=2π,相邻最高点和最低点的横坐标间的距离为π。根据勾股定理可得最高点和最低点之间的距离为5.D 6.B 7.D 提示:当k=0时,α=,α的终边位于第一象限;当k=1时,α=,α的终边位于第二象限;当k=2时,α=,α的终边位于y轴的非正半轴上;当k=3时,α=2π+的终边位于第一象限。 8.D 提示:将函数y=sin(6x +)图像上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数y=sin(2x +)的图像,再沿x轴向右平移个单位长度,得到函数y==sin2x的图像。由2x=kπ(k∈Z),得x=(k∈Z),故函数y=sin2x的图像的一个对称中心是(,0)。 9.B 10.C 11.D 提示:由于任意的a∈(-∞,0),可知acosx0≤a恒成立等价于cosx0≥1恒成立,故cosx0=1,可 知 x0=2kπ,k∈ Z。 所 以。 12.A 13.B 提示:由题意可知g(x)=2sinωx(ω>0)。由 g(x)在≤2。 14.C 15.B 提示:由图像过点对任意x∈R恒成立,可知当x=1时,函数f(x)取到最大值,即2kπ,k∈Z,解得ω=4+24k,k∈Z。因为ω>0,所以ω的最小值为4。 16.C 17.D 18.D 19.C 提示:令sinπx0=0,得πx0=kπ(k∈Z),故零点x0=k(k∈Z)。由此可得-29,…,0,1,2,…,29,30,31时,不等式|x0|+f(x0+)<33成立;当x0=32时,f(32 +)=1,32+1<33不成立,故x0≠32;当x0=33时,f(33 +)=-1,33-1<33成立,故x0=33是零点。同理可知,x0=-32不是零点,x0=-33是零点。综上可知,零点个数为65。
二、填空题

三、解答题
24.提示:(1)函数fx()=sin2x+φ()+1(-π<φ<0)图像的一个对称中心的坐标为,k∈Z,所以φ=
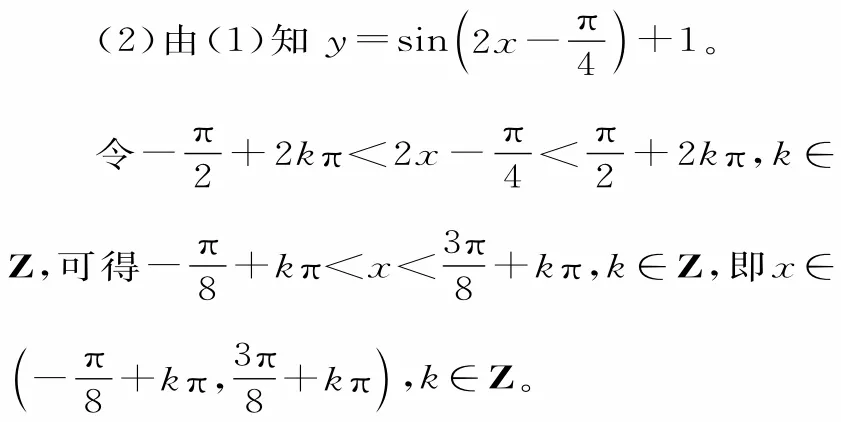
说明:此题的第(2)问的答案也可写成闭区间的形式。





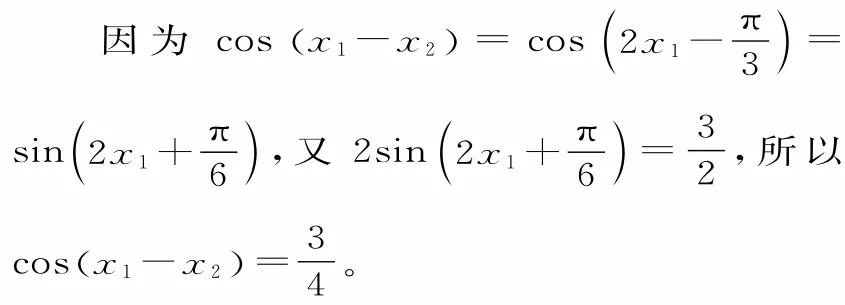
28.提示:(1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π),根据条件①,可知这个函数的周期是12。
由②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200。
由③可知,f(x)在[2,8]上单调递增,且f(2)=100,所以f(8)=500。
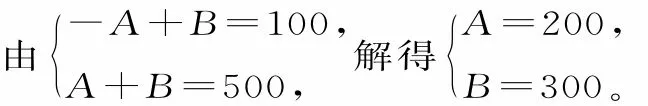
根据分析可知,当x=2时,f(x)最小,当x=8时,f(x)最大,故所以φ=-

因为x∈N*,且1≤x≤12,故x=6,7,8,9,10,即只有6,7,8,9,10这5个月要准备400份以上的食物。

