求三角函数的单调区间易错点剖析
2018-05-08 09:52华腾飞
中学生数理化·高一版 2018年4期
■华腾飞
在求三角函数的单调区间时,由于对概念和法则理解不清、把握不准,常常会导致错解的发生。下面举例分类剖析,希望能引起同学们的注意,以避免此类错误的发生。
一、忽视基本函数致错

剖析:要参照基本函数y=sinx,就必须把自变量x的系数化为正数,这是因为曲线y=sin(-3x)已由曲线y=sinx经过了沿x轴的翻折变换。

注意:上述两种解法的结果看似不同,这只不过是形式不同而已,其实质上是相同的。
二、忽视函数的定义域致错
错解:因为对数函数y=lgz是单调递增函数,所以只需求出z=sin(3x -)的单调递增区间即可。

剖析:求复合函数的单调区间时,不能忽视函数的定义域。

三、忽视复合函数的单调区间致错

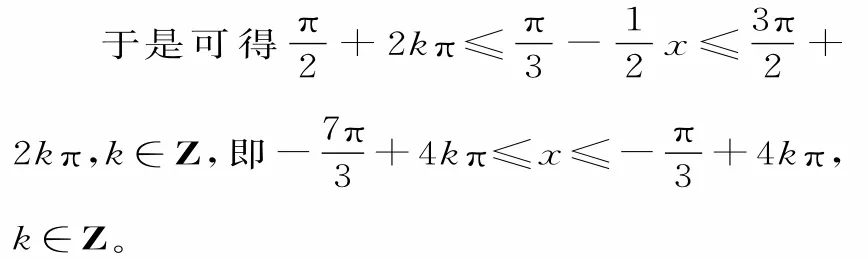
四、忽视题设条件致错

剖析:由题意可知,只需求出区间(-2π,2π)内的递增区间即可。

五、忽视参数的取值符号致错
例5 讨论函数y=acosx+b的单调区间。
错解:当函数y=cosx单调递增,即x∈[2kπ-π,2kπ](k∈Z)时,所求函数单调递增;
当函数y=cosx单调递减,即x∈[2kπ,2kπ+π](k∈Z)时,所求函数单调递减。
剖析:对含参数问题,若参数的取值符号不确定,则必须对参数进行讨论。上述解法是由于想当然地认为a>0导致错解的。
正解:当a=0时,y=b为常函数,这时没有单调区间;
当a>0时,所求函数的递增区间为[2kπ-π,2kπ](k∈Z),递减区间为[2kπ,2kπ+π](k∈Z);
当a<0时,所求函数的递增区间为[2kπ,2kπ+π](k∈Z),递减区间为[2kπ-π,2kπ](k∈Z)。
猜你喜欢
中学生数理化·七年级数学人教版(2022年6期)2022-06-05
语数外学习·高中版上旬(2022年2期)2022-04-09
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-12-04
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
数理化解题研究(2020年19期)2020-07-22
读写算(2019年5期)2019-09-01
中学生数理化·七年级数学人教版(2019年12期)2019-05-21
中学课程辅导·教学研究(2017年29期)2018-02-26

