三角函数诱导公式的应用
■朱 承
三角函数诱导公式的重要作用在于,它揭示了终边在不同象限但具有一定对称关系(关于原点、坐标轴或直线y=±x对称)的角的三角函数间的内在联系,从而可以将任意角的三角函数转化到一个较小的特定范围来研究。
一、知角求值型问题
例 1 求 sin(-1200°)cos1290°+cos(-1020°)sin(-1050°)的值。
分析:利用诱导公式进行角的变换。
解:原 式 =-sin1200°cos1290°-cos1020°sin1050°=-sin(3×360°+120°)·cos(3×360°+210°)-cos(2×360°+300°)·sin(2×360°+330°)=-sin120°cos210°-cos300°sin330°=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)sin(360°-30°)=sin60°·
评注:知角求值,要分析特殊角和待求角之间的联系,设法用特殊角通过诱导公式表示待求角。
二、知式求值型问题
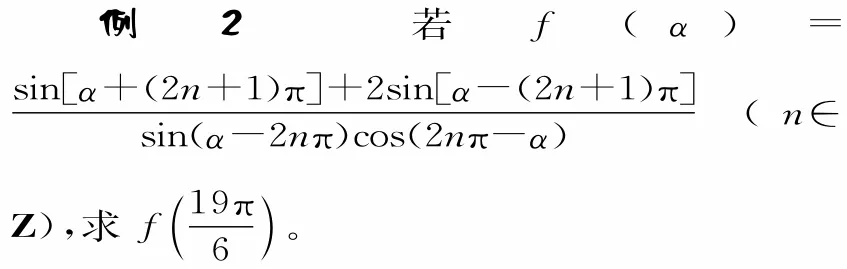
分析:先利用三角函数的诱导公式将所给的三角函数式化简,再求值。
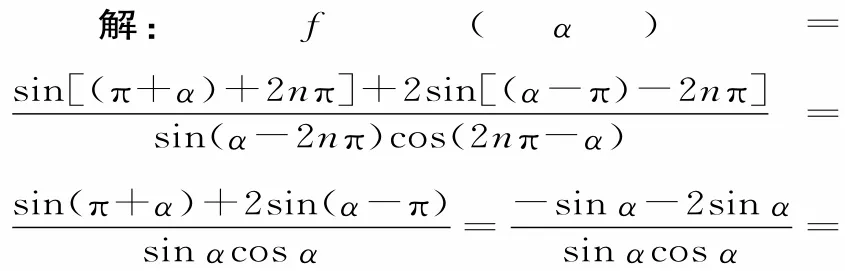

评注:求解这类问题时,一般应从变形化简开始,只有从所涉及的角中分离出2π的整数倍,才能运用诱导公式。三角函数式的化简求值,一定要注意公式的正确运用,有时是直接运用,有时则需化简后运用。
三、知值求值型问题

分析:先对所求三角函数与已知的三角函数中的角进行比较,再采用整体分析的方法,建立角与角之间的联系。
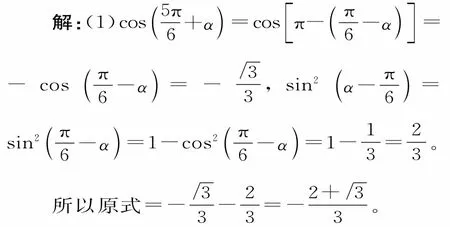
(2)cos(15°-α)=sin[90°-(15°-α)]=sin(75°+α)。因α 是第三象限角,所以sin(75°+ α)< 0,sin(75° + α)=sin[-90°+(75°+α)]=-sin[90°-(75°+α)]=
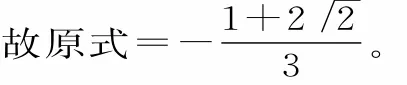
评注:整体观察角的结构特征,将所求的三角函数值中的角转化为所给角与特殊角的和与差的形式,实现由未知向已知的转化。

