求解A,ω,φ的值,确定y=Asinωx+φ()的解析式
2018-05-08 09:51■李琳
中学生数理化·高一版 2018年4期
■李 琳
■李 琳
1.A,ω,φ的常规求法
2.确定函数y=Asinωx+φ()的解析式要注意的两个问题
(1)求参数的顺序问题:A,ω,φ三个参数均可以通过特殊点的代入进行求解,利用图像的最大值与最小值来确定A的值,根据对称轴与对称中心的距离确定T,进而求出ω,最后通过代入一个特殊点来确定φ的值。
(2)求φ值时特殊点的选取:优先选择最值点,因为通过最值点计算出的φ值往往是唯一的,不会出现多解的情况。如果代入其他点(如零点),有时要面临结果取舍的问题。
例1 已知函数y=Asin(ωx+φ)+m(A>0,0<φ<)的最大值为4,最小值为0,两条对称轴之间的最短距离为,直线x=是其图像的一条对称轴,则函数的解析式为 。


例2 已知A,B,C,D,E是函数y=sin(ωx+φ)(ω>0,0<φ<)在一个周期内的图像上的五个点,如图1所示,其中点 A为为y轴上的点,C为图像上的最低点,E为该图像的一个对称中心,B,D关于点E中心对称,线段CD在x轴上的投影长为,则函数的解析式为____。
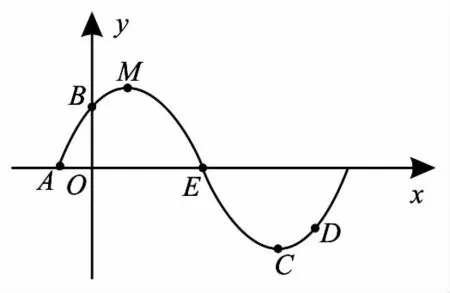
图1
解:设图像的最高点为M,可知点M,C关于点E中心对称,点B,D关于点E中心对称,所以线段BM与CD关于点E中心对称,所以线段BM在x轴上的投影长也为。

猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
中学生数理化·七年级数学人教版(2017年10期)2017-04-23
福建中学数学(2016年2期)2016-10-19
数学大王·低年级(2016年10期)2016-09-10
上海大学学报(自然科学版)(2011年3期)2011-01-31
中学生数理化·七年级数学北师大版(2008年6期)2008-10-22

