盘点三角函数重难点
■范运灵
一、任意角
重难点主要有任意角的概念、终边相同的角、角的终边对称问题、象限角的确定、区域角的表示和任意角的应用等。
例 1 求所有与角-210°终边相同的角的集合,并求出其中的最小正角、最大负角。
分析:写出角的集合→给k赋值→确定符合条件的角。
因为 -210°=-360°+150°,所以与-210°终边相同的角的集合为{α|α=k·360°+150°,k∈Z}。其中最小正角为150°,最大负角为-210°。
注意:①α为任意角;②k·360°与α之间是“+”号,k·360°-α可理解为k·360°+(-α);③相等的角终边一定相同,终边相同的角不一定相等,终边相同的角有无数个,它们相差360°的整数倍;④k∈Z这一条件不能少。
二、任意角的三角函数
重难点主要有三角函数定义的应用、三角函数的定义域和值域、三角函数在各象限内的符号、三角函数线的应用、用单位圆解决三角函数问题等。
分析:求出sinα→分类讨论各种情况。
当y=0时,sinα=0,cosα=-1,tanα=0。

①三角函数值是比值,是一个实数,其大小和点P(x,y)在终边上的位置无关,只与角α的终边位置有关。②符号sinα、cosα或tanα是一个整体,离开“α”,“sin”“cos”或“tan”不表示任何意义,更不能把“sinα”当成“sin”与“α”的乘积。③诱导公式的实质是说终边相同的角的同一三角函数值相等,作用是把求任意角的三角函数值转化为求0~2π(或0°~360°)之间的角的三角函数值。
三、同角三角函数的基本关系
重难点主要有利用同角三角函数的基本关系求值、化简、证明,弦切互化,与sinα±cosα,sinαcosα有关的求值,与参数有关的三角函数问题。
(sinβ-cosβ)2=1-2sinβcosβ=
因为sinβcosβ<0且0<β<π,所以sinβ>0,cosβ<0。于是sinβ-cosβ=。
①灵活运用公式(sinα±cosα)2=1±2sinα·cosα求解。②同角三角函数的基本关系式揭示了“同角不同名”的三角函数的运算规律,它的精髓在“同角”二字上,如sin22α+cos22α=1=tan8α等都成立。③已知角α的某一种三角函数值,求角α的其余三角函数值时,要注意选择合理的公式。一般先选用平方关系,再用商数关系。在应用平方关系求sinα或cosα时,其正、负号是由角α所在的象限决定的,切不可凭想象乱写公式。进行三角函数式的求值时,要细心观察题目的特征,灵活、恰当地选用公式,统一角、统一函数、降低次数是三角函数关系变形的出发点。
四、三角函数的图像与性质
重难点主要有正(余)弦、正切函数图像的作法和性质,定义域、值域及正(余)弦函数的最值,与其他函数的综合运用。
例 4 已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图像关调函数,求ω和φ的值。
分析:求出φ值→得出k,ω的范围→分类讨论所有情况。
因为f(x)是偶函数,所以y轴是其对称轴,即x=0时函数取得最大值或最小值。故f(0)=sinφ=±1。又因0≤φ≤π,故φ=。由f(x)的k∈Z。

①正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础。②“五点法”是画三角函数图像的基本方法,与“五点法”作图有关的问题是高考常考的试题。
五、函数y=Asin(ωx+φ)的图像
重难点主要有φ、ω、A(φ≠0,ω>0且ω≠1,A>0且A≠1)对y=Asin(ωx+φ),x∈R的图像的影响,y=sinx的图像与y=Asin(ωx+φ)的图像的关系,函数y=Asin(ωx+φ)(A>0,ω>0)的各量的物理意义,以及由图像确定函数y=Asin(ωx+φ)的解析式。
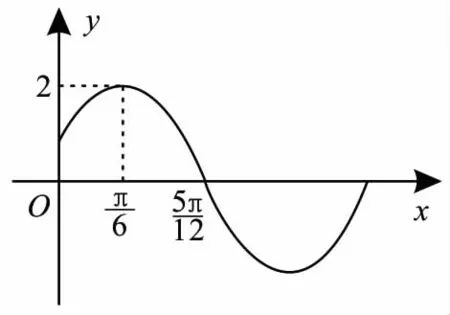
图1
(1)求函数f(x)的解析式。
(2)如何由函数y=2sinx的图像通过适当的变换得到函数f(x)的图像,写出变换过程。
分析:(1)根据图像推出ω和f(x)的解析式。(2)根据三角函数变换法则进行变换。

由y=sinx的图像通过变换可得到函数y=Asin(ωx+φ)的图像,其变化途径有两条:一y=Asin(ωx+φ)。
三角函数的重难点除上文提到的外,还有三角函数的诱导公式,也是一个难点,同学们在学习时应注意以下几点:①明确各诱导公式的作用:公式一的作用是将任意角转化为0~2π之间的角求值,公式二的作用是将0~2π之间的角转化为0~π之间的角求值,公式三的作用是将负角转化为正角求值,公式四是将角转化为0~之间的角求值。②诱导公式的记忆口诀是“角变名不变,符号看象限”,其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号。将α看成锐角,只是为了方便公式记忆,实际上α可以是任意角。诱导公式可以统一概括为“k·±α(k∈Z)”的诱导公式。当k为偶数时,得α的同名函数值;当k为奇数时,得α的异名函数值,在前面加一个把α看成锐角时原函数值的符号。诱导公式统一成“k·±α(k∈Z)”后,记忆口诀为“奇变偶不变,符号看象限”。
提示:因为角α是第二象限角,所以k·360°+90°<α<k·360°+180°(k∈Z),即2k·360°+180°<2α<2k·360°+360°(k∈Z),故2α是第三或第四象限角或终边在y轴的非正半轴上。因为k·180°+45°<<k·180°+90°(k∈Z),当k为偶数时,在第一象限,当k为奇数时在第三象限,故为第一或第三象限角。


