品味三角函数的创新问题

■郑 欣

三角函数自身的交汇以及与其他知识的交汇已成为高考的热点问题,本文聚焦之。

创新1:三角函数的定义与直线斜率的交汇

解:利用直线与圆相交的圆心角确定点到直线的距离,求出直线斜率,再利用三角函数的定义和同角关系求解。

品味:借助三角函数的定义和同角三角函数的基本关系,将三角函数与直线和圆相交问题有机地交汇是本题的一大特点,其中斜率和倾斜角是沟通关系的桥梁。

变式训练1:若直线x+y-2=0与直线x-y=0的交点P在角α的终边上,则tanα的值为____。

提示:由x+y-2=0和x-y=0,解得交点P(1 ,1 ,),所以tanα==1。

创新2:三角函数图像与最值的交汇

例 2 已知函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x=π时,函数f(x)取得最小值,则下列结论正确的是( )。

A.f(2)＜f(-2)＜f(0)

B.f(0)＜f(2)＜f(-2)

C.f(-2)＜f(0)＜f(2)

D.f(2)＜f(0)＜f(-2)

要比较f(2),f(-2),f(0)的大小,只需判断横坐标为2,-2,0与最近的最高点处对称轴的距离大小。易知0,2与比较近,-2与-0.6,所以f2()＜f-2()＜f0()。应选A。

品味:求三角函数解析式中的参数的一般步骤:通过周期确定ω;通过最值或对称中心确定初相φ;通过最值确定A。三角函数的比较大小问题,需要通过图像来判断,本题代入函数值不方便,根据函数值在图像中的具体位置进行判断,凸显图像的应用价值。

创新3:三角函数的有界性与最值的交汇

解法1:利用正弦函数的有界性,构建不等式求出最值。

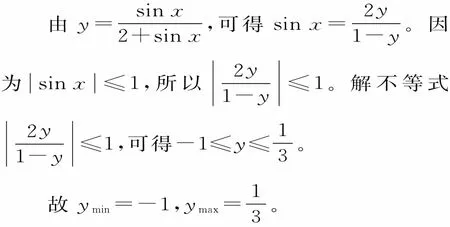
解法2:分式类函数可化为部分分式,利用正弦函数的有界性求最值。

当sinx=-1时,得ymin=-1;当

故yminmax=-1,y=

创新4:三角函数的图像与性质的综合应用

例 4 已知函数f(x)=2sin(ωx+φ)-1(ω＞0,|φ|＜π)的一个零点是x=,其图像上一条对称轴方程为x=-,则当ω取最小值时,下列说法正确的是____。(填写所有正确说法的序号)

解:由零点和对称轴及ω＞0,|φ|＜π确定函数的解析式,依据y=Asin(ωx+φ)+B的图像与性质逐一验证。

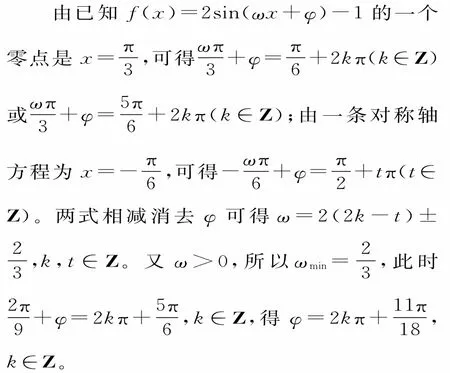
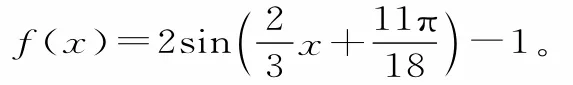
品味:关于y=Asin(ωx+φ)和y=Acos(ωx+φ)的多项选择问题,可先求出解析式,再利用正弦和余弦函数的单调区间的子集或对称轴或对称中心进行判断。本题的解答过程凸显三角函数中“整体变量观念”的应用。

创新5:三角函数的性质与求值的交汇

A.4030 B.4032

C.4033 D.4035

解:由正弦函数的周期定义可得此函数的周期为4,可知一个周期内的4个函数值的和

品味:巧用三角函数的周期性和对称性是解答本题的关键。

变式训练5:(1)函数f(x)=Asin(ωx+φ)+b的部分图像如图1所示,则f(1)+f(2)+…+f(2012)的值为 。

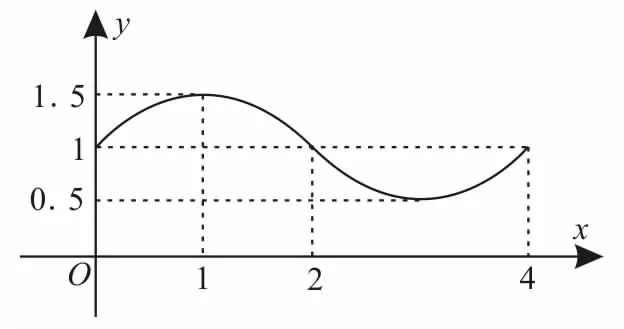
图1

创新6:三角函数与二次函数的交汇

例6 函数f(x)=sin2x+的最大值是____,最小值是____。

解:利用三角函数的平方关系,转化为二次函数的值域问题求解。

品味:形如y=asinxcosx+b(sinx±cosx)+c的三角函数最值问题,可先设t=sinx±cosx,再转化为关于t的二次函数问题求最值,但要注意新元的取值范围,即新函数的定义域。

变式训练6:(1)函数y=cos2x-sin2x+2sinx的最大值为 。

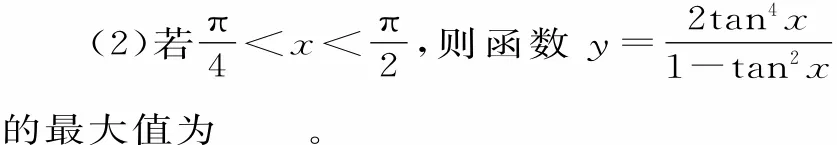
提示:(1)令t=sinx,则-1≤t≤1。由于y=cos2x-sin2x+2sinx=-2sin2x+所以当t=时,函数y=cos2x-sin2x+2sinx取得最大值,其最大值为

创新7:三角函数的图像与方程的根的交汇

解:作出已知分段函数的图像(如图2),借助图像及函数值相等,利用三角函数的对称轴可简化求解。

图2

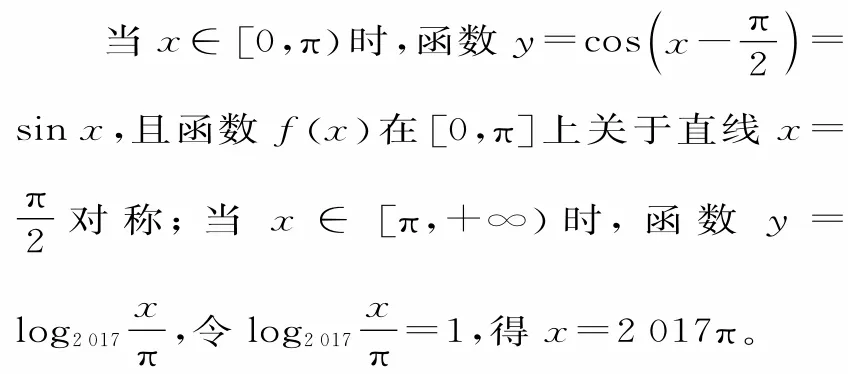
因为f(a)=f(b)=f(c),所以a+b=π,c∈ (π,2017π),可得a+b+c=π+c∈(2π,2018π)。

品味:本题的解题过程体现了数形结合思想方法与“化难为简”方法的具体应用。

图3

创新8:三角函数与不等式的交汇

例 8 将函数y=sinx的图像上所有点的横坐标缩短到原来的(纵坐标不变),再将所得的图像向左平移个单位长度后得到函数f(x)的图像。

(1)写出函数f(x)的解析式。

解:(1)注意图像的变换过程,依据题设得y=sinx→y=sin2x→y=sin(2x +)为所求的函数解析式。

(2)通过换元,把所求问题转化为二次不等式在区间上的恒成立问题求解。

设函数g(t)=t2-mt-1,t∈[0,1],则g(t)的图像是开口向上的一段抛物线。要使g(t)≤0恒成立,当且仅当可得m≥0,所以m的取值范围是0,+∞[)。

品味:本题也可以利用分离参数法求解:t2-mt-1≤0,t∈[0,1],当t=0时不等式恒成立;当t∈(0,1]时,m≥t-,令g(t)=t-,则g(t)在 (0,1]上是增函数,可得g(t)≤g(1)=1-1=0,即得m≥0。

创新9:三角函数与几何概型的交汇

品味:借助图像的平移和诱导公式化简解析式,构建区间长度为测度,利用三角不等式求区间内的概率,使得三角函数与几何概型有机地交汇,体现了命题创新的特点。

创新10:三角函数与新定义的交汇

解:理解新定义的意义,其实质就是求正、余弦函数中的函数值较大的函数。注意它们的周期都为2π的特征,只需研究在[0 ,2 π]上正、余弦函数中的函数值较大的函数(图像),可利用函数图像求最小值。

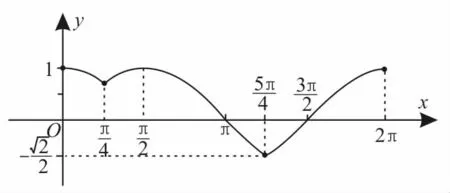
图4

品味:三角函数与新定义问题的交汇属于高考的新颖命题,近几年高考已逐步淡化了对复杂三角变换和特殊技巧变换的考查,而重点转移对三角函数的图像与性质的考查,因此应引起同学们的重视。