基于高频数据的我国国债期货市场套利研究

杨艳军 陈思岑

一、引 言

国债期货在帮助市场参与者管理利率风险以及推动我国利率市场化改革等方面都起着重要作用。20世纪90年代，我国曾短暂推出过国债期货合约，但由于当时利率市场化的时机尚未成熟，加之交易和监管制度不够完善，在发生了一系列市场违规事件后被监管机构叫停。2013年9月6日，阔别市场18年之久的5年期国债期货重新上市；2015年3月20日，10年期国债期货也重启交易。截至今日，5年期国债期货和10年期国债期货运行平稳，交易活跃，已经成为我国期货市场中的重要交易品种。

伴随着市场参与者和交易量的不断增长，我国5年期国债期货和10年期国债期货的流动性有了长足的提高，这为进行基于国债期货的套利交易提供了客观条件。作为期货市场套利交易策略的重要组成部分之一，跨品种套利交易在关联品种间价格变动导致其价差偏离均衡关系时进行，一般在同一交易所的不同品种、但相同月份的合约之间操作。

二、文献综述

（一）国外相关研究

Working（1949）基于期货的仓储功能首次提出了期货套利交易的概念。他认为套利行为是价格投机的复杂形式，但当时的研究仅限于同种期货合约不同交割期限的跨期限套利。在期货套利方法的研究方面，Eagle和Granger（1987）最早提出了协整的概念来解决时间序列非平稳旳问题，并提出了检验非平稳变量之间协整关系的两步法，即协整检验方法。他认为，如果两个非平稳序列存在着一个稳定的线性关系，则显示了这两个序列之间存在协整的关系。Johansen和Juselius（1988,1990）提出了基于VAR模型的Johansen协整检验方法，修正了Eagle和Granger两步法的缺陷。Balke和Fomby（1997）富有创新性的提出了门限协整，即两个资产价格经过基本验证不存在协整关系，但在它们价格波动的趋势中存在一定的门限，在这个门限内却不存在协整关系，然而在一定的门限外却存在协整关系。门限协整的提出进一步扩大了协整理论在实际中的应用范围。Carmona和Durrleman（2003）将期货套利主要的类型总结为：不同期货品种的跨品种套利（Inter-Commodity Spread），同种交易品种的跨市场套利（Inter-Market Spread），以及同种交易品种的跨期限套利（Calendar Spread）等。

（二）国内相关研究

杨艳军（2007）研究了我国主要期货品种的流动性特征，指出流动性是开展套利的基础。丁秀玲、华仁海（2007）选取大连商品交易所的大豆和豆粕为研究对象，运用Johnsen协整检验等方法，认证得到两者之间存在长期均衡关系，最后结果显示，使用误差修正模型的模拟套利分析结果不显著。韩广哲和陈守东（2007）选取上证50指数为研究对象，并运用统计套利模型对其进行分析，发现在测试样本上统计套利模型的夏普比为1.3，最后结果证实，指数研究上也适用于统计套利模型。康瑞强（2009）选取上海期货交易所上市的铜合约为研究对象，运用基于协整理论的统计套利策略，对5分钟高频数据的实证对象进行协整检验，最后证实长期均衡关系存在于所选取的铜合约之间。殷晓梅等（2009）选取大连商品交易所的大豆和豆粕期货合约为研究对象，通过运用基于协整理论的误差修正模型和趋势套利模型，结果证实该种模型进行套利分析的结果明显，同时发现两种套利模型可以互补使用。张连华（2011）首次选取国内的股指期货和现货为研究对象，运用基于协整的统计套利思想，结果证实模型适用并实现了套利。戴进（2012）选取股指期货和ETF的期限套利为研究对象，引入协整统计套利理论，通过对ETF与IF300配对交易机会的分析，证实了一定的期现套利空间存在于ETF与股指期货之间。谢佳新（2013）用统计套利的思想进行了程序化套利交易模型设计，并以豆油期货和棕榈油期货进行了实证。

国内外现有的研究对于商品期货和股指期货的关注远多于国债期货，对跨期限套利和期货现货套利的研究也多于跨品种套利；虽然形成了以协整理论为主的期货套利研究体系，但是在套利模型建立和套利收益分析等方面还没有成熟的研究方法。从2013年5年期国债期货重新上市至今不足5年的时间，我国目前对于国债期货的学术研究整体而言还不丰富。根据协整理论，本文使用基于日内高频数据的GARCH模型构建套利方案，对我国5年期国债期货和10年期国债期货进行跨品种套利研究，对于理论发展和实际应用均有一定的意义。

三、数据、理论及模型

进行套利实证研究可以分为以下几个步骤：第一，套利对象的选取，包括选择具体金融产品、时间序列的时间范围、时间序列的频率等；第二，相关性、平稳性、协整检验；第三，建立GARCH模型，用以预测时间序列的异方差性；第四，基于GARCH模型设计套利方案，估计套利模型参数；第五，对样本外数据进行套利模型的有效性验证。

（一）选取套利对象

20世纪90年代，我国曾短暂开展过国债期货交易，但由于发生了数次严重的违规事件而被监管机构叫停，因此这段时间内的国债期货合约研究价值不大。2013年9月6日，我国5年期国债期货首先重启交易；2015年3月20日我国10年期国债期货于重新上市后，才形成了5年期和10年期国债期货两个交易品种。因此，选择2015年3月20日至2018年2月28日的5年期国债期货和10年期国债期货合约作为套利对象。在数据的频率方面，选择5年期国债期货当季连续合约和10年期国债期货当季连续合约的1分钟收盘价（f5和f10）作为具体的研究对象，获得195840组共391680个数据，以分析基于高频数据的国债期货套利机会。其中，2015年3月20日至2017年3月20日的数据用于估计模型参数，2017年3月21日至2018年2月28日的数据用于样本外检验。

（二）相关性、平稳性、协整检验

套利统计的基础建立在两个或多个随机变量之间存在较高的相关性，通过构建这几个变量的组合使得该组合趋于某一特定关系。样本内数据选取2015年3月20日至2017年3月20日的5年期国债期货当季连续合约和10年期国债期货当季连续合约的1分钟收盘价共133008组、266016个数据。从图1可以看出，5年期国债期货当季连续合约和10年期国债期货当季连续合约的价格走势十分相似。

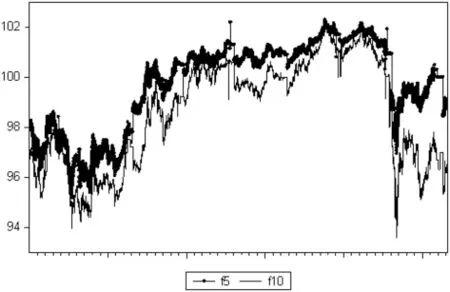
图1 f5和f10走势图

相关性分析是对两个或多个变量之间相互关系的方向和程度进行分析。相关系数的计算公式如下：

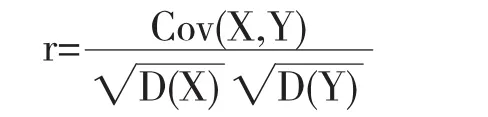
其中，Cov(X,Y)为两个变量X和Y的协方差，D(X)、D(Y)分别为X和Y的方差。相关系数r的取值范围是-1≤r≤1，如果r＞0为正相关，r＜0则为负相关。

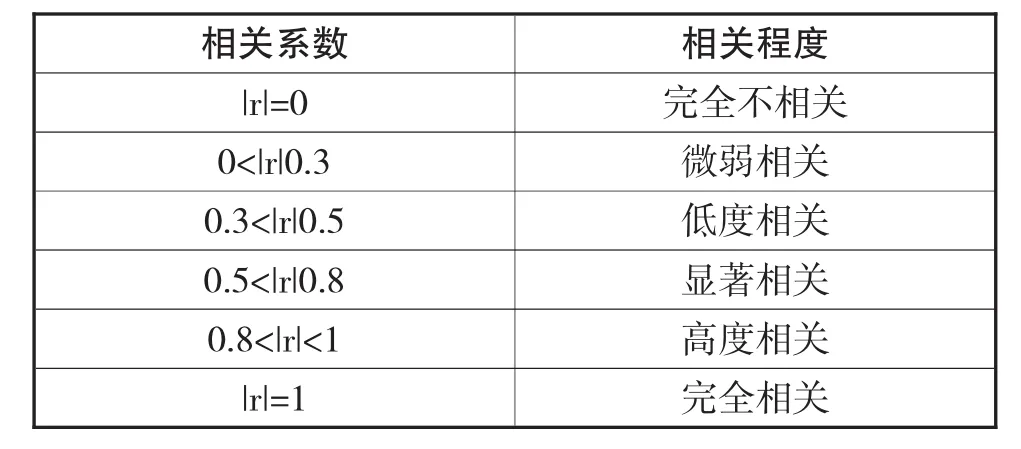
表1 相关系数和相关程度对应表

对样本内数据进行相关性分析，两个序列的相关系数达到0.961573。该相关系数远远大于一般比较系数0.8，说明两个序列是高度正相关的。

表2 f5和f10的相关系数

时间序列的平稳性是进行统计套利的前提。判定时间序列是否平稳的依据，就是判断其统计特征是否随时间的变化而变化。单位根检验是对时间序列平稳性的检验，只有平稳的时间序列，才能进行计量分析，否则会出现伪回归现象。单位根检验常用的方法有DF检验法、ADF检验、PP检验等、KPSS检验等六种，本文将采用ADF检验法（Augmented Dickey-Fuller test）来检验5年期国债期货和10年期国债期货样本内时间序列的平稳性。

ADF检验是通过检验序列中是否存在单位根来判断序列的平稳性，如果该序列平稳则说明不存在单位根，如果存在单位根则说明该序列不平稳。ADF检验法一般有以下三种检验模型。

模型1：序列不含常数项

模型2：序列含常数项

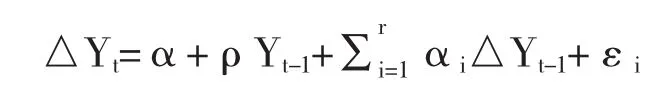
模型3：序列含趋势项

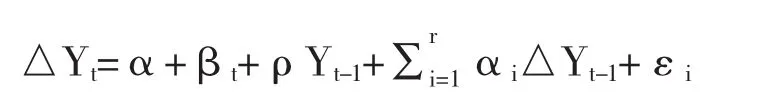
模型原假设为序列存在一个单位根；备选假设为不存在单位根序列。对于上述三个回归模型，原假设为ρ=0，即存在单位根，备选假设为ρ＜0，则不存在单位根。我们通过比较1%、5%和10%三个置信水平下的临界值与序列的ADF值之间的大小关系来判断检验结果。如果三个置信水平下的临界值均大于ADF值，可以说明检验拒绝原假设，即时间序列是平稳的，该序列可设为I(0)序列。如果三个置信水平下的临界值均小于ADF值，则接受原假设，那也就是说检验的时间序列具有单位根，即时间序列非平稳。在此情况下，需要继续对非平稳时间序列进行差分处理，然后继而运用ADF检验对进行差分处理后的序列进行检验，一直到序列平稳，即没有单位根为止。如果经过d阶差分处理后序列变为平稳的，那么称此序列为d阶单整序列，记为I(d)。

使用Eviews软件对两个时间序列（f5和f10）的样本内数据进行ADF检验的结果如下：

表3 f5和f10的ADF检验结果

5年期国债期货和10年期国债期货价格的时间序列不平稳，而它们的一阶差分的时间序列平稳，可以证实5年期国债期货和10年期国债期货价的时间序列是一阶单整的I（1）序列，存在长期协整的可能性。

Engle和Granger在1978年提出的协整理论认为一些经济变量之间存在长期稳定的均衡关系，因此可以从资产组合的短期价值偏差中获取套利机会。如果两个变量都是单整变量，只有当他们的单整阶数相同时，才可能协整；如果他们的单整阶数不同，则不可能协整。这种协整检验的具体做法就是对两个变量回归方程的残差进行单位根检验。

对于两个一阶单整序列，要按照E-G两步法进行协整检验的步骤如下：第一步，用普通最小二乘法（OLS）构建序列的回归方程

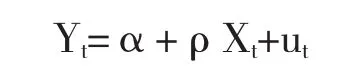
计算非均衡误差，得到：

本文使用E-G两步法对5年期国债期货和10年期国债期货的样本内价格序列进行协整检验。使用最小二乘法（OLS）对5年期国债期货和10年期国债期货的样本内价格序列构建回归方程，Eviews软件得出二者的静态回归方程如下；

对以上回归结果中的残差进行ADF检验，显示其ADF值为-4.541356，小于1%显著水平下的临界值，可以拒绝该序列有单位根的原假设，即接受残差序列是平稳的。5年期国债期货和10年期国债期货价格序列存在协整关系，两个品种间可以进行统计套利。

秦铁崖想了想，最终妥协：“你们两位，一老一少，老的太老，小的太小，都不是江湖中人，去是可以去，只能在一旁帮衬，主阵必须由我来打。战书是下给江云飞的，我代江云飞而来，由我打头阵，理所当然。”

（三）建立GARCH模型

在实际市场环境中，金融时间序列呈现出方差时变的特性，这种特性也被称为“异方差性”。金融时间序列的异方差性意味着采用常数方差的金融模型存在先天性的弱点，能够考虑时变方差的模型才能够真实反映金融市场情况。Engle（1982）开创性地提出自回归条件异方差模型（Autoregressive Conditional Heteroscedasticity Model，ARCH） 的 概 念 ，Bollerslev(1986)对其进行了扩展提出广义自回归条件异方差（Generalized ARCH，GARCH）模型。在此之后，一些学者对GARCH模型作出了进一步改进，提出了非对称性GARCH模型、TARCH和EGARCH等，这些模型统称为ARCH模型族。ARCH模型族被广泛应用于经济学的多个领域，描述金融时间序列的波动性特征。而GARCH模型适合在计算量不大时，方便地描述高阶的ARCH过程，因而具有更大的适用性。

在标准化的GARCH（1,1）模型中：

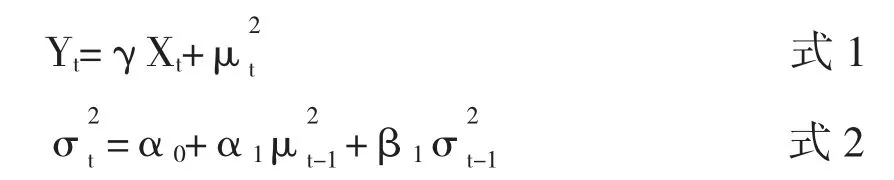
其中，Xt为1*(k+1)维外生变量，γ是1*(k+1)维系数向量，式1的均值方程是一个带有误差项的外生变量函数，式2则是条件方差方程。

将金融时间序列的波动集群性考虑到模型中是GARCH模型创新意义的价值所在。残差的方差往往是依赖于以前时刻的方差，所以用GARCH模型能够更加精确地进行预测。本文使用GARCH模型来研究价差序列残差的方差，从而设计出5年期国债期货和10年期国债期货的统计方案。

5年期国债期货和10年期国债期货价格序列的协整关系显示：二者之间存在着简单的线性关系。二者的价差序列可以表示为：

对5年期国债期货和10年期国债期货价格序列的残差Spread进行去中心化，得到：

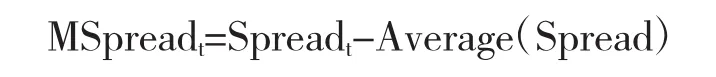
使用Eviews软件对MSpreadt进行自相关和偏自相关分析，呈现出自相关系数拖尾、偏自相关系数截尾的现象，因此判断MSpreadt是一个AR（1）过程。

用OLS法对MSpreadt建立模型如下：

对残差序列MSpreadt的随机波动项μt进行滞后1阶的ARCH-LM检验，可判断MSpreadt存在ARCH效应。对MSpreadt构建GARCH(1,1)模型，结果显示ARCH、GARCH和常数项都通过了t检验，这说明该模型能够更好地拟合样本内数据。以和σt来代表残差序列的方差和标准差，可得到方差方程和标准差方程：

（四）设计套利模型

残差序列MSpreadt是去中心化之后的时间序列，具有围绕0上下波动的属性。当MSpreadt偏离0值达到一定程度时，有回归0值的趋势。用残差序列的标准差σt来衡量偏离程度，可以针对MSpreadt/σt值设计一套明确的开仓和平仓规则。当MSpreadt/σt偏离到特定程度后，通过构建5年期国债期货和10年期国债期货的资产组合进行开仓——即买入低估值的期货合约，并卖出相应数量的高估值的期货合约，以期望MSpreadt/σt偏离程度减小；开仓后，若MSpreadt/σt偏离程度减小到一定程度，通过对开仓的资产组合进行反向平盘以锁定收益——即卖出原先买入的合约并买入原先卖出的合约，称为获利平仓；开仓后，若MSpreadt/σt的偏离继续增大到一定程度，通过对开仓的资产组合进行反向平盘以锁定损失——即卖出原先买入的合约并买入原先卖出的合约，称为止损平仓。其中，当MSpreadt/σt偏离达到特定的正值引发的套利行为称为“正向套利”，当MSpreadt/σt偏离值达到特定的负值引发的套利行为称为“反向套利”。

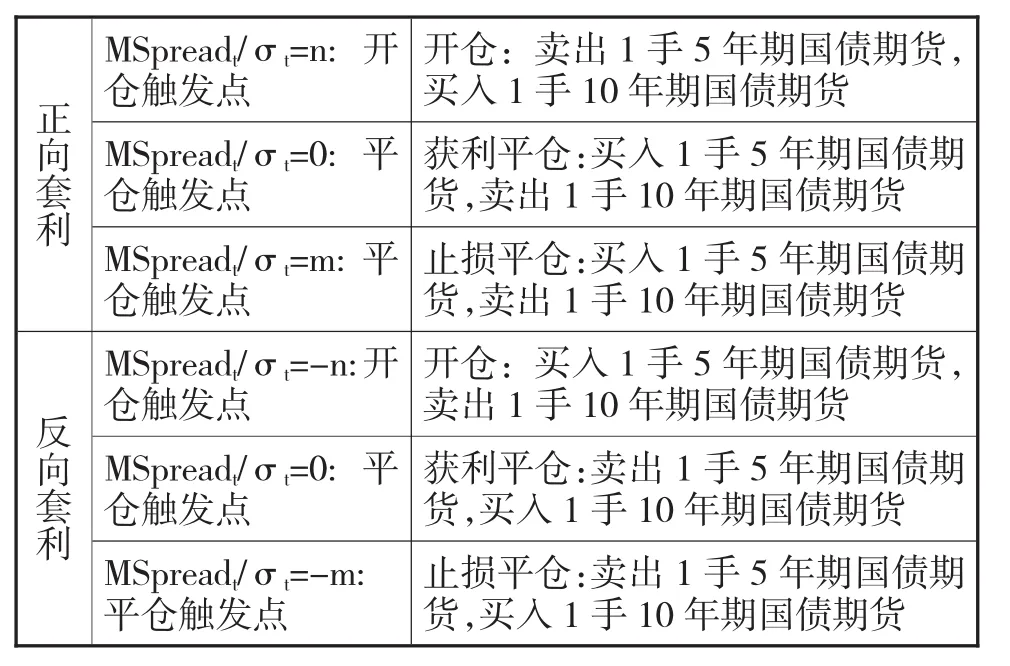
表4 正、反向套利示意表(m＞n＞0)

根据GARCH模型MSpreadt序列时变方差的推导，我们可以绘出2015年3月20日至2017年3月20日之间的MSpreadt/σt走势图。从图中可以看出，MSpreadt/σt围绕着0值上下波动，在偏离达到一定程度后有明显回归0值的趋势。当MSpreadt/σt＞0时，5年期国债期货合约的价格被高估，10年期国债期货合约的价格被低估，可以建立起5年期国债期货合约空头和10年期国债期货合约多头的资产组合，以期望合约价格回归；当MSpreadt/σt＜0时，5年期国债期货合约的价格被低估，10年期国债期货合约的价格被高估，可以建立起5年期国债期货合约多头和10年期国债期货合约空头的资产组合，以期望合约价格回归。

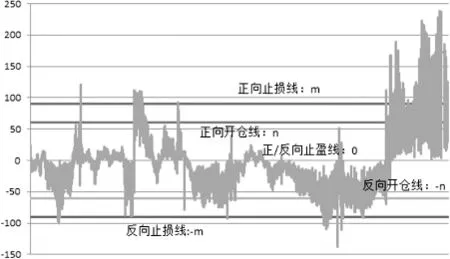
图2 样本内数据开、平仓示意图

根据MSpreadt/σt建立套利方案主要涉及到三个取值的设定：MSpreadt/σt开仓值、MSpreadt/σt止盈值、MSpreadt/σt止损值。由于MSpreadt/σt有向0值回归的天然特征，MSpreadt/σt止盈值可以设定为0，即无论是正向套利还是反向套利，最终均以MSpreadt/σt回归 0值作为止盈条件；假定MSpreadt/σt的开仓值为n，交易中的一般经验是将止损值m设置为小于|2n|的数值（如|1.5n|），这样可以使止损时的亏损程度（|2n-1.5n|=|0.5n|）小于止盈时的收益程度（|n-0|=|n|），保证闭合的交易产生正期望收益。这里，我们将止损值m统一设定为1.5n。分别将 MSpreadt/σt的开仓值 n 选取为 2、6、10、20、60、100，止损平仓值 m=1.5n 相应为 3、9、15、30、90、150，止盈平仓值为0，套利方案未考虑交易成本的绝对收益情况如下：

表5 开仓值n与套利收益的关系

套利方案的收益和开仓值n并不呈现简单的同向或反向关系。当n值较小时，可导致套利方案中的频繁开仓，同时止盈和止损的频率也大大提高，且每次止盈获得的收益均不高；当n值较大时，套利方案的开仓、止盈、止损频率降低，每次止盈获得收益大幅提高，但同样止损的亏损程度也相应增大。在我们选取的6个n值中，当n=60，即正反向套利的开仓触发点为MSpreadt/σt=±60、止损平仓触发点为MSpreadt/σt= ±90、 止 盈 平 仓 触 发 点 为MSpreadt/σt=0时，进行套利获得的未考虑交易成本的绝对收益最大，达到5.59%。

（五）样本外数据检验

样本外数据选取2017年3月21日至2018年2月28日的5年期国债期货当季连续合约和10年期国债期货当季连续合约的1分钟收盘价共62832组、125664个数据，对于设计的基于GARCH模型的套利方案进行检验。同样将正反向套利的开仓触发点设定为MSpreadt/σt=±60、止损平仓触发点设定为MSpreadt/σt=±90、止盈平仓触发点设定为MSpreadt/σt=0。

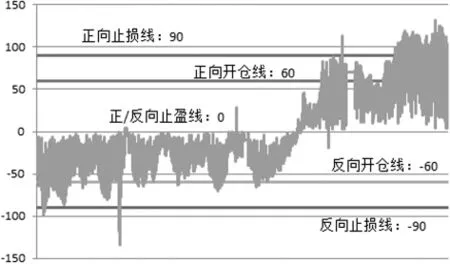
图3 样本外数据开、平仓示意图

经过检验，本文设计的基于GARCH模型的套利方案在样本外数据中获得了未考虑交易成本的绝对收益4.56%。

四、总 结

本文旨在研究我国5年期国债期货和10年期国债期货之间的跨品种套利关系，选取2015年3月20日10年期国债上市以来5年期国债期货和10年期国债期货连续合约的1分钟收盘价作为高频数据，检验其相关性、平稳性和协整性，并使用GARCH模型设计基于时间序列异方差性的统计套利方案。对于样本内数据，选取数个不同的正反向套利的开仓触发点和止损平仓触发点进行套利分析，发现当选取正反向套利的开仓触发点为MSpreadt/σt=±60、止损平仓触发点为MSpreadt/σt=±90、止盈平仓触发点为MSpreadt/σt=0时，进行套利获得的未考虑交易成本的绝对收益最大，达到5.59%；随后选取同样的开仓触发点、止损平仓触发点和止盈平仓触发点，对样本外数据进行套利分析，获得了未考虑交易成本的绝对收益4.56%，证明了套利方法的有效性。

【参考文献】

［1］Engle,Grange.Cointegration and error correction:representation,estimation and testing.Econometrica.1987.55:251-276

［2］Johansen,S.,K.Juselius.Maximum Likelihood Estimation and Inference on Cointegration with Applications to the Demand for Money.Oxford Bulletin of Economics and Statistics.1990.52:169-210

［3］Balke N S,Fomby T B.Threshold Cointegration.International Economics Reviews.1997.38:627-645.

［4］杨艳军.期货市场流动性理论与方法实证.北京：知识产权出版.2007

［5］韩广哲，陈守东.统计套利模型研究——基于上证50指数成份股的检验.数理统计与管理.2007.26（5）908-916

［6］宋颖.国债期货价格套利机会的实证分析——以美国国债期货市场为例.价格理论与实践.2012（08）68-69

［7］朱丽荣，苏辛，周勇.基于我国期货市场的跨期套利研究. 运筹与管理.2015.24（3）179-188